Punkty 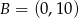 i
i 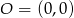 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 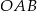 , w którym
, w którym 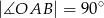 . Przyprostokątna
. Przyprostokątna 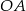 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 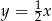 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 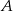 i długość przyprostokątnej
i długość przyprostokątnej 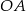 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt
Dany jest okrąg o równaniu 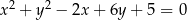 .
.
- Napisz równania stycznych do danego okręgu, prostopadłych do prostej o równaniu
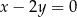 .
. - Oblicz pole trójkąta
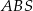 , gdzie
, gdzie 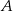 i
i 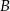 są punktami przecięcia się stycznych z prostą o równaniu
są punktami przecięcia się stycznych z prostą o równaniu 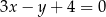 , zaś
, zaś 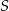 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Wierzchołkami trójkąta 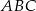 są środki okręgów określonych równaniami
są środki okręgów określonych równaniami 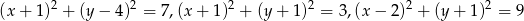 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Punkty 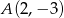 i
i 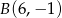 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 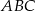 , którego pole jest równe 10. Wyznacz współrzędne wierzchołka
, którego pole jest równe 10. Wyznacz współrzędne wierzchołka 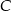 .
.
Odcinek 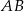 , gdzie
, gdzie 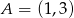 i
i 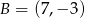 , jest podstawą trójkąta
, jest podstawą trójkąta 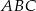 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 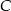 tak, aby trójkąt
tak, aby trójkąt 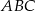 był równoramienny, a jego pole było równe 30.
był równoramienny, a jego pole było równe 30.
Prosta 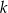 tworzy z dodatnią półosią
tworzy z dodatnią półosią 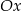 kąt o mierze
kąt o mierze 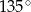 i przechodzi przez punkt
i przechodzi przez punkt 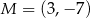 . Prosta
. Prosta 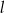 jest prostopadła do prostej
jest prostopadła do prostej 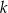 i przecina oś
i przecina oś 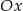 w punkcie o odciętej
w punkcie o odciętej 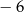 . Oblicz obwód trójkąta utworzonego przez proste
. Oblicz obwód trójkąta utworzonego przez proste 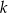 ,
, 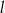 i oś
i oś 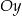 .
.
Wyznacz współrzędne środka ciężkości trójkąta w zależności od współrzędnych jego wierzchołków.
Punkt 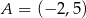 jest jednym z wierzchołków trójkąta równoramiennego
jest jednym z wierzchołków trójkąta równoramiennego 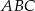 , w którym
, w którym 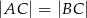 . Pole tego trójkąta jest równe 15. Bok
. Pole tego trójkąta jest równe 15. Bok 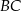 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 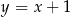 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 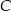 .
.
Wierzchołki 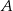 i
i 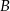 trójkąta prostokątnego
trójkąta prostokątnego 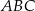 leżą na osi
leżą na osi 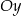 układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków
układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków 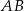 ,
, 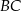 i
i 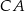 w punktach – odpowiednio –
w punktach – odpowiednio – 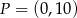 ,
, 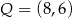 i
i 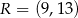 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 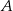 ,
, 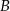 i
i 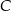 tego trójkąta.
tego trójkąta.
Wierzchołki 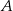 i
i 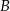 trójkąta prostokątnego
trójkąta prostokątnego 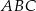 leżą na prostej
leżą na prostej 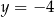 . Okrąg wpisany w ten trójkąt jest styczny do boków
. Okrąg wpisany w ten trójkąt jest styczny do boków 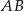 ,
, 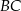 i
i 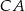 odpowiednio w punktach
odpowiednio w punktach 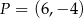 ,
, 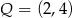 i
i 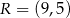 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 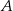 ,
, 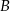 i
i 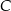 tego trójkąta.
tego trójkąta.
W trójkącie prostokątnym 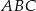 , gdzie
, gdzie 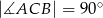 , wierzchołek
, wierzchołek 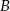 ma współrzędne
ma współrzędne 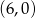 . Prosta
. Prosta 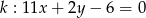 , zawierająca środkową trójkąta poprowadzoną z wierzchołka
, zawierająca środkową trójkąta poprowadzoną z wierzchołka 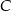 , przecina bok
, przecina bok 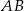 trójkąta w punkcie
trójkąta w punkcie 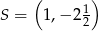 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 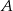 i
i 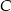 .
.
W trójkącie równoramiennym 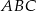 o podstawie
o podstawie 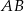 poprowadzono wysokość z wierzchołka
poprowadzono wysokość z wierzchołka 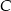 . Wyznacz równanie prostej zawierającej tę wysokość, jeśli
. Wyznacz równanie prostej zawierającej tę wysokość, jeśli 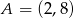 ,
, 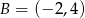 .
.
Punkty 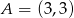 i
i 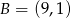 są wierzchołkami trójkąta
są wierzchołkami trójkąta 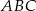 , a punkt
, a punkt 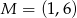 jest środkiem boku
jest środkiem boku 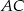 . Oblicz współrzędne punktu przecięcia prostej
. Oblicz współrzędne punktu przecięcia prostej 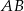 z wysokością tego trójkąta, poprowadzoną z wierzchołka
z wysokością tego trójkąta, poprowadzoną z wierzchołka 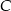 .
.
Odcinek 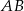 jest wysokością trójkąta równobocznego. Oblicz długość boku trójkąta, jeśli wiadomo, że
jest wysokością trójkąta równobocznego. Oblicz długość boku trójkąta, jeśli wiadomo, że 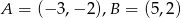
Wyznacz równanie symetralnej przeciwprostokątnej trójkąta prostokątnego o wierzchołkach 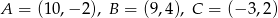 .
.
Dane są dwa wierzchołki trójkąta 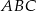 :
: 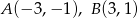 . Punkt
. Punkt 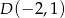 należy do boku
należy do boku 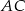 , a odcinek
, a odcinek 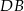 jest środkową w trójkącie
jest środkową w trójkącie 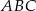 . Oblicz:
. Oblicz:
- współrzędne wierzchołka
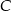 ;
; - pole trójkąta
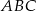 .
.
Punkty 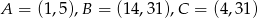 są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka 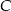 przecina prostą
przecina prostą 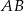 w punkcie
w punkcie 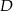 . Oblicz długość odcinka
. Oblicz długość odcinka 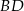 .
.
Punkty 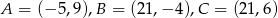 są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Prosta zawierająca wysokość tego trójkąta poprowadzona z wierzchołka 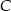 przecina prostą
przecina prostą 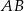 w punkcie
w punkcie 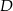 . Oblicz długość odcinka
. Oblicz długość odcinka 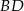 .
.
Punkt 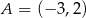 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 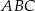 , w którym
, w którym 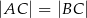 . Pole tego trójkąta jest równe 15. Bok
. Pole tego trójkąta jest równe 15. Bok 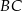 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 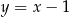 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 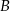 i
i 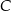 tego trójkąta.
tego trójkąta.
Punkt 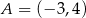 jest wierzchołkiem rozwartokątnego trójkąta równoramiennego
jest wierzchołkiem rozwartokątnego trójkąta równoramiennego 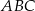 , w którym
, w którym 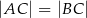 . Pole tego trójkąta jest równe 17,5 i wszystkie jego wierzchołki mają współrzędne całkowite. Bok
. Pole tego trójkąta jest równe 17,5 i wszystkie jego wierzchołki mają współrzędne całkowite. Bok 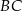 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 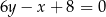 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 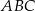 .
.
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 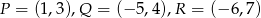 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 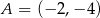 oraz
oraz 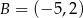 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 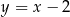 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Podstawą trójkąta równoramiennego 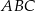 jest bok
jest bok 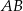 , gdzie
, gdzie 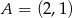 i
i 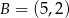 . Ramię tego trójkąta zawiera się w prostej o równaniu
. Ramię tego trójkąta zawiera się w prostej o równaniu 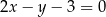 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 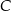 .
.
Dany jest trójkąt równoramienny 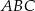 , w którym
, w którym 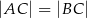 . Ponadto wiadomo, że
. Ponadto wiadomo, że 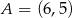 i
i 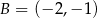 . Wierzchołek
. Wierzchołek 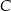 należy do osi
należy do osi 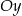 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 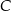 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 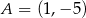 oraz
oraz 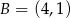 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 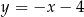 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Punkt 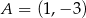 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 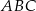 , w którym
, w którym 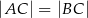 . Punkt
. Punkt 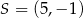 jest środkiem odcinka
jest środkiem odcinka 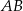 . Wierzchołek
. Wierzchołek 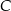 tego trójkąta leży na prostej o równaniu
tego trójkąta leży na prostej o równaniu 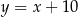 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków  i
i  tego trójkąta.
tego trójkąta.
Dany jest trójkąt równoramienny 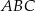 , w którym
, w którym 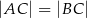 . Ponadto wiadomo, że
. Ponadto wiadomo, że 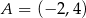 i
i 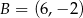 . Wierzchołek
. Wierzchołek 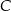 należy do osi
należy do osi 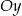 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 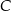 .
.
Podstawą trójkąta równoramiennego 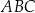 jest odcinek o końcach w punktach
jest odcinek o końcach w punktach 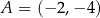 oraz
oraz 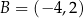 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 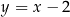 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 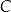 .
.
W kartezjańskim układzie współrzędnych  punkt
punkt 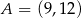 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 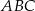 . Prosta
. Prosta 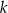 o równaniu
o równaniu 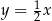 zawiera dwusieczną kąta
zawiera dwusieczną kąta 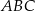 tego trójkąta. Okrąg
tego trójkąta. Okrąg 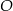 o równaniu
o równaniu 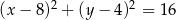 jest wpisany w ten trójkąt. Oblicz współrzędne punktu styczności prostej przechodzącej przez wierzchołki
jest wpisany w ten trójkąt. Oblicz współrzędne punktu styczności prostej przechodzącej przez wierzchołki 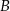 i
i 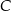 tego trójkąta z okręgiem
tego trójkąta z okręgiem 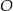 .
.
Oblicz pole trójkąta ograniczonego prostą 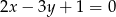 i osiami układu współrzędnych.
i osiami układu współrzędnych.

