Punkty 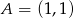 i
i 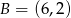 są wierzchołkami trójkąta
są wierzchołkami trójkąta 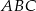 . Wysokości trójkąta
. Wysokości trójkąta 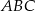 przecinają się w punkcie
przecinają się w punkcie 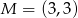 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt
Punkt 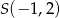 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie  . Wierzchołek
. Wierzchołek  ma współrzędne
ma współrzędne 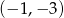 , a bok
, a bok 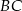 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 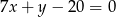 . Oblicz pole trójkąta
. Oblicz pole trójkąta 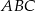 .
.
W układzie współrzędnych punkty 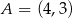 i
i 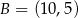 są wierzchołkami trójkąta
są wierzchołkami trójkąta 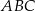 . Wierzchołek
. Wierzchołek 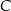 leży na prostej o równaniu
leży na prostej o równaniu 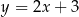 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 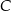 , dla którego kąt
, dla którego kąt 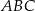 jest prosty.
jest prosty.
W układzie współrzędnych punkty 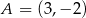 i
i 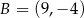 są wierzchołkami trójkąta
są wierzchołkami trójkąta 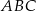 . Wierzchołek
. Wierzchołek 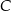 leży na prostej o równaniu
leży na prostej o równaniu 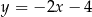 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 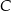 , dla którego kąt
, dla którego kąt 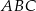 jest prosty.
jest prosty.
Punkty 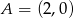 i
i 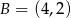 leżą na okręgu o równaniu
leżą na okręgu o równaniu 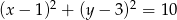 . Wyznacz na tym okręgu taki punkt
. Wyznacz na tym okręgu taki punkt 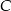 , aby trójkąt
, aby trójkąt 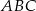 był trójkątem równoramiennym o podstawie
był trójkątem równoramiennym o podstawie 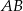 .
.
Dane są punkty 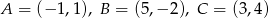 .
.
- Wyznacz równanie prostej przechodzącej przez punkt
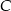 i prostopadłej do prostej
i prostopadłej do prostej 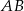 .
. - Oblicz pole trójkąta
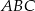 .
.
Punkty 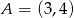 ,
, 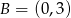 i
i 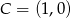 należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.
należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.
Punkty 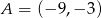 i
i 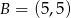 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 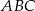 , w którym
, w którym 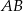 jest przeciwprostokątną. Wyznacz współrzędne wierzchołka
jest przeciwprostokątną. Wyznacz współrzędne wierzchołka 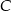 wiedząc, że leży on na osi
wiedząc, że leży on na osi 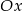 .
.
Punkty 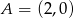 i
i 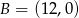 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 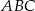 o przeciwprostokątnej
o przeciwprostokątnej 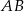 . Wierzchołek
. Wierzchołek 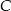 leży na prostej o równaniu
leży na prostej o równaniu 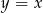 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 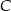 .
.
Punkty 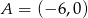 i
i 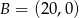 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 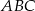 o przeciwprostokątnej
o przeciwprostokątnej 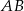 . Wierzchołek
. Wierzchołek 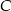 leży na prostej o równaniu
leży na prostej o równaniu 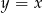 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 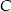 .
.
Wierzchołki trójkąta 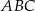 mają współrzędne:
mają współrzędne: 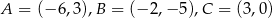 . Okrąg
. Okrąg  jest styczny do prostej
jest styczny do prostej 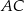 , a jego środek jest punktem przecięcia się wysokości trójkąta
, a jego środek jest punktem przecięcia się wysokości trójkąta 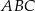 . Okrąg
. Okrąg  przecina prostą
przecina prostą 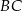 w punkcie
w punkcie 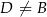 . Oblicz iloraz
. Oblicz iloraz 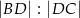 .
.
Dany jest okrąg 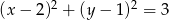 . Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
. Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
Wierzchołki trójkąta 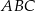 mają współrzędne:
mają współrzędne: 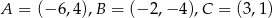 . Napisz równanie okręgu, który jest styczny do prostej
. Napisz równanie okręgu, który jest styczny do prostej 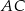 , a jego środek jest punktem przecięcia się wysokości trójkąta
, a jego środek jest punktem przecięcia się wysokości trójkąta 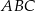 .
.
Boki 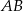 i
i 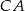 trójkąta
trójkąta 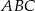 są zawarte w prostych
są zawarte w prostych 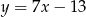 i
i 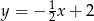 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 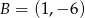 i
i 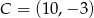 . Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok
. Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok 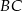 .
.
Punkt 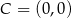 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 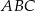 , którego wierzchołek
, którego wierzchołek 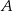 leży na osi
leży na osi 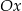 , a wierzchołek
, a wierzchołek 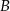 na osi
na osi 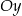 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 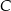 przecina przeciwprostokątną
przecina przeciwprostokątną 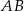 w punkcie
w punkcie 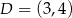 .
.
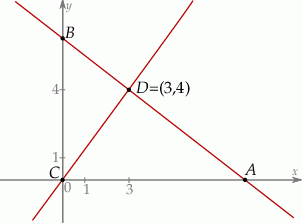
Oblicz współrzędne wierzchołków  i
i  tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej  .
.
Punkt 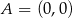 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 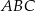 , którego wierzchołek
, którego wierzchołek 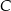 leży na osi
leży na osi 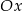 , a wierzchołek
, a wierzchołek 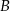 na osi
na osi 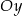 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 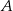 przecina przeciwprostokątną
przecina przeciwprostokątną 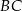 w punkcie
w punkcie 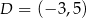 .
.
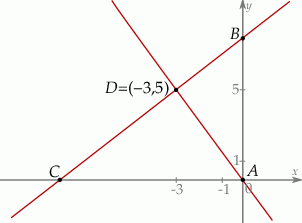
Oblicz współrzędne wierzchołków  i
i  tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej 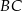 .
.
Dane są wierzchołki trójkąta 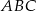 :
: 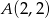 ,
, 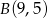 i
i 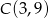 . Z wierzchołka
. Z wierzchołka 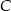 poprowadzono wysokość tego trójkąta, która przecina bok
poprowadzono wysokość tego trójkąta, która przecina bok 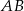 w punkcie
w punkcie 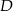 . Wyznacz równanie prostej przechodzącej przez punkt
. Wyznacz równanie prostej przechodzącej przez punkt 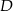 i równoległej do boku
i równoległej do boku 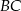 .
.
W kartezjańskim układzie współrzędnych 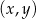 punkt
punkt 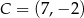 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 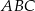 . Prosta
. Prosta 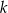 o równaniu
o równaniu 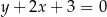 zawiera dwusieczną kąta
zawiera dwusieczną kąta 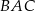 tego trójkąta. Okrąg
tego trójkąta. Okrąg 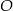 o równaniu
o równaniu 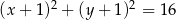 jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków
jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków 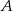 i
i 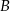 trójkąta
trójkąta 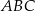 .
.
Wierzchołkami trójkąta 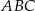 są punkty
są punkty 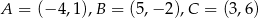 . Oblicz długość środkowej
. Oblicz długość środkowej 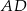 .
.
Wierzchołkami trójkąta 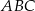 są punkty
są punkty 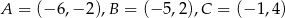 . Oblicz długość środkowej
. Oblicz długość środkowej 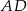 .
.
Dany jest trójkąt 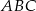 o wierzchołkach
o wierzchołkach 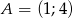 ,
, 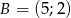 ,
, 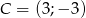 .
.
- Napisz równanie wysokości opuszczonej z wierzchołka
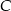 na bok
na bok 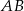 .
. - Napisz równanie środkowej boku
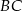 .
. - Napisz równanie symetralnej boku
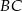 .
. - Oblicz obwód i pole tego trójkąta.
Wykaż, że trójkąt 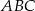 o wierzchołkach
o wierzchołkach 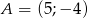 ,
, 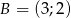 ,
, 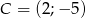 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt o wierzchołkach 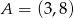 ,
, 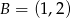 ,
, 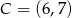 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt o wierzchołkach 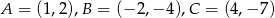 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Wykaż, że trójkąt 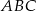 o wierzchołkach
o wierzchołkach 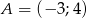 ,
, 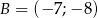 ,
, 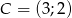 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt 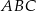 o wierzchołkach
o wierzchołkach 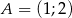 ,
, 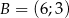 ,
, 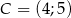 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt 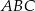 o wierzchołkach
o wierzchołkach 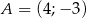 ,
, 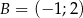 ,
, 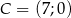 jest prostokątny.
jest prostokątny.
Punkt 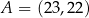 jest wierzchołkiem trójkąta prostokątnego o polu
jest wierzchołkiem trójkąta prostokątnego o polu 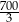 . Prosta
. Prosta 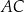 zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną
zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną 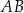 ma równanie
ma równanie 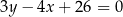 . Środek okręgu wpisanego w trójkąt
. Środek okręgu wpisanego w trójkąt 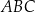 ma współrzędne
ma współrzędne 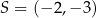 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 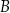 i
i 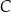 tego trójkąta.
tego trójkąta.
Wierzchołek 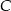 trójkąta
trójkąta 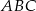 leży na prostej
leży na prostej 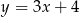 , a pozostałe wierzchołki mają współrzędne
, a pozostałe wierzchołki mają współrzędne 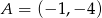 i
i 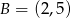 . Uzasadnij, że pole trójkąta
. Uzasadnij, że pole trójkąta 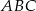 nie zależy od wyboru punktu
nie zależy od wyboru punktu 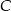 i oblicz to pole.
i oblicz to pole.
Ostrokątny trójkąt równoramienny 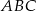 o podstawie
o podstawie 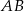 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 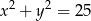 . Punkty
. Punkty 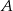 i
i 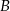 leżą na prostej o równaniu
leżą na prostej o równaniu 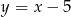 .
.
- Oblicz współrzędne punktów:
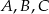 .
. - Oblicz kąty trójkąta
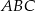 .
.

