Podstawy trapezu równoramiennego o polu 40 mają długości 6 i 14. Oblicz długość ramienia tego trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez
Podstawy trapezu mają długości 4 i 8. Kąty, jakie tworzą ramiona z dłuższą podstawą, mają miary 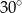 i
i 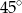 . Oblicz pole trapezu.
. Oblicz pole trapezu.
W trapezie, którego podstawy mają długości 10 cm i 4 cm, miary kątów przy dłuższej podstawie wynoszą 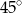 i
i 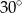 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
W trapezie, którego podstawy mają długości 12 cm i 6 cm, miary kątów przy dłuższej podstawie wynoszą 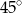 i
i 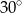 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Podstawy trapezu 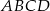 mają długości
mają długości 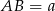 i
i 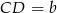 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 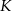 i
i 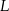 w ten sposób, że odcinek
w ten sposób, że odcinek 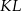 jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka
jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka 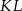 .
.
Na trapezie 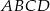 można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe
można opisać okrąg. Jedna z jego podstaw jest dwa razy dłuższa od drugiej, a przekątna dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego ple jest równe 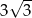 .
.
W trapezie równoramiennym jedna z podstaw jest dwa razy dłuższa od drugiej, a przekątna trapezu dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego pole jest równe 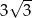 .
.
W trapezie równoramiennym stosunek długości podstaw jest równy 3:4, a przekątna trapezu dzieli kąt przy dłuższej podstawie na połowy. Oblicz długości boków trapezu wiedząc, że jego pole jest równe 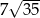 .
.
W trapezie 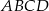 (
(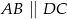 ) przekątne
) przekątne 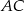 i
i 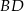 przecinają się w punkcie
przecinają się w punkcie 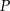 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 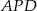 jest równe polu trójkąta
jest równe polu trójkąta 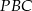 .
.
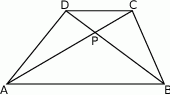
Punkt 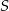 jest środkiem okręgu wpisanego w trapez
jest środkiem okręgu wpisanego w trapez 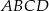 (
(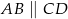 ). Wykaż, że trójkąt
). Wykaż, że trójkąt 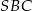 jest prostokątny.
jest prostokątny.
Dany jest trapez, w którym podstawy mają długość 4 cm i 10 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 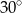 i
i 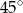 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
Dany jest trapez, w którym podstawy mają długość 6 cm i 20 cm oraz ramiona tworzą z dłuższą podstawą kąty o miarach 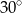 i
i 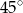 . Oblicz wysokość tego trapezu.
. Oblicz wysokość tego trapezu.
Dany jest trapez prostokątny 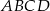 , gdzie
, gdzie 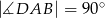 ,
, 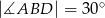 ,
, 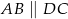 ,
, 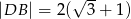 i
i 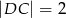 .
.
- Oblicz długość promienia okręgu wpisanego w trójkąt
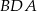 .
. - Wyznacz sumę kwadratów sinusów kątów wewnętrznych trapezu
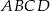 .
.
Pole trapezu jest równe 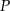 , a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
, a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
W trapezie 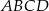 podstawy
podstawy 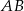 i
i 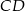 oraz ramię
oraz ramię 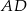 mają długości odpowiednio 15 cm, 12 cm i 6 cm. O ile centymetrów należy przedłużyć ramię
mają długości odpowiednio 15 cm, 12 cm i 6 cm. O ile centymetrów należy przedłużyć ramię 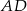 , by przecięło się z przedłużeniem ramienia
, by przecięło się z przedłużeniem ramienia 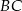 ?
?
Oblicz wysokość trapezu o podstawach długości 18 i 14 oraz ramionach długości 3.
W trapezie równoramiennym, który nie jest równoległobokiem, ramię ma długość 7 cm, a przekątna 8 cm. Oblicz długości podstaw trapezu wiedząc, że odcinek łączący środki ramion trapezu ma długość 4 cm.
Na trapezie opisano okrąg o średnicy długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc, że przekątna tego trapezu ma długość 20 cm, oblicz pole tego trapezu.
W trapezie równoramiennym długość krótszej podstawy wynosi 9 cm, przekątnej 17 cm a ramienia 10 cm. Oblicz jego pole.
Dany jest trapez opisany na okręgu, którego kąty przy jednej podstawie są ostre, oraz którego pole jest równe 168. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów jeżeli ramiona trapezu mają długości 13 i 15.
Punkt 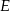 leży na ramieniu
leży na ramieniu 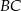 trapezu
trapezu 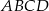 , w którym
, w którym 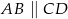 . Udowodnij, że
. Udowodnij, że 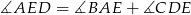 .
.
Trapez równoramienny 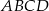 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 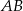 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 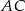 i
i 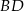 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 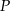 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 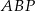 .
.
Trapez równoramienny 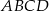 o ramieniu długości 7 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 7 wpisany jest w okrąg, przy czym dłuższa podstawa 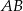 trapezu, o długości 14, jest średnicą tego okręgu. Przekątne
trapezu, o długości 14, jest średnicą tego okręgu. Przekątne 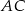 i
i 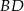 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 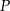 . Oblicz długość okręgu wpisanego w trójkąt
. Oblicz długość okręgu wpisanego w trójkąt 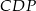 .
.
W trapez wpisano okrąg. Punkt styczności okręgu z dłuższą podstawą trapezu dzieli tę podstawę na odcinki długości 2,5 dm i 4 dm. Wysokość trapezu ma długość 4 dm. Oblicz obwód tego trapezu.
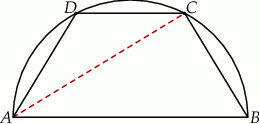
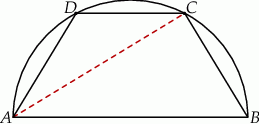
W półkole o promieniu  wpisano trapez równoramienny o krótszej podstawie długości
wpisano trapez równoramienny o krótszej podstawie długości  . Oblicz długość przekątnej trapezu.
. Oblicz długość przekątnej trapezu.
W półkole o promieniu  wpisano trapez równoramienny o przekątnej długości
wpisano trapez równoramienny o przekątnej długości 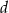 . Oblicz długość krótszej podstawy trapezu.
. Oblicz długość krótszej podstawy trapezu.