Dany jest trapez prostokątny 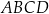 o kątach prostych przy wierzchołkach
o kątach prostych przy wierzchołkach 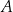 i
i 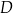 . Ramię
. Ramię 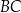 trapezu ma długość 5. W ten trapez wpisano okrąg o środku w punkcie
trapezu ma długość 5. W ten trapez wpisano okrąg o środku w punkcie 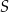 i promieniu 2. Punkt
i promieniu 2. Punkt 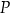 jest punktem styczności tego okręgu i dłuższej podstawy
jest punktem styczności tego okręgu i dłuższej podstawy 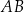 tego trapezu (zobacz rysunek).
tego trapezu (zobacz rysunek).
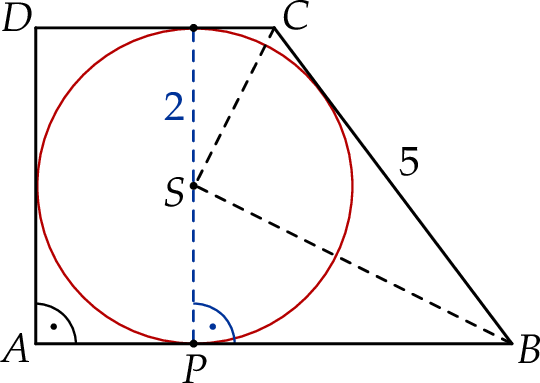
Wykaż, że trójkąty 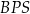 i
i 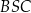 są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa.
są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa.

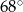 , a różnica miar dwóch pozostałych kątów jest równa
, a różnica miar dwóch pozostałych kątów jest równa 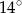 . Oblicz miary kątów tego trapezu.
. Oblicz miary kątów tego trapezu. 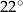 . Oblicz pole trapezu, przyjmując, że
. Oblicz pole trapezu, przyjmując, że 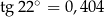 .
. 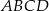 (
(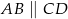 ,
, 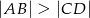 ) jest wpisany w okrąg o promieniu długości
) jest wpisany w okrąg o promieniu długości 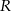 . Wiadomo że kąt ostry trapezu ma miarę
. Wiadomo że kąt ostry trapezu ma miarę  zaś
zaś 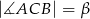 , gdzie
, gdzie 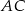 jest przekątną trapezu. Oblicz długość
jest przekątną trapezu. Oblicz długość  dłuższej podstawy tego trapezu oraz długość
dłuższej podstawy tego trapezu oraz długość 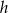 jego wysokości.
jego wysokości.  , a przekątna ma długość 12.
, a przekątna ma długość 12. 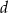 i ramieniu długości
i ramieniu długości  jest opisany na okręgu. Wykaż, że odległość środka okręgu wpisanego w ten trapez od końca krótszej podstawy jest równa
jest opisany na okręgu. Wykaż, że odległość środka okręgu wpisanego w ten trapez od końca krótszej podstawy jest równa 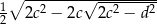 .
. 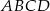 boki nierównoległe
boki nierównoległe 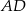 i
i 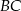 zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane
zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane 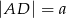 oraz
oraz 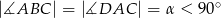 .
. 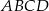 o podstawach
o podstawach 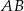 i
i 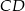 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 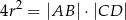 .
.  i
i 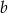 , gdzie
, gdzie 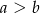 .
.  opisano trapez równoramienny, którego długość jednej z podstaw wynosi
opisano trapez równoramienny, którego długość jednej z podstaw wynosi 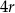 . Oblicz odległość środka okręgu od wierzchołków trapezu.
. Oblicz odległość środka okręgu od wierzchołków trapezu. 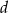 i tworzy z dłuższą podstawą kąt o mierze
i tworzy z dłuższą podstawą kąt o mierze  . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu. 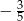 . Oblicz długość ramienia tego trapezu.
. Oblicz długość ramienia tego trapezu. 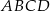 w ten sposób, że podstawa
w ten sposób, że podstawa 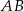 jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.
jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu. 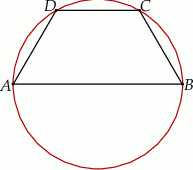
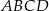 o podstawach
o podstawach 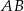 i
i 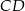 przekątne
przekątne 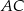 oraz
oraz 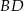 przecinają się w punkcie
przecinają się w punkcie 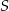 . Wykaż, że jeżeli
. Wykaż, że jeżeli 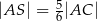 , to pole trójkąta
, to pole trójkąta 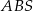 jest 25 razy większe od pola trójkąta
jest 25 razy większe od pola trójkąta 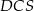 .
. 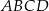 o podstawach
o podstawach 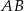 i
i 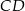 przekątne
przekątne 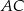 oraz
oraz 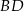 przecinają się w punkcie
przecinają się w punkcie 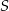 . Wykaż, że jeżeli
. Wykaż, że jeżeli 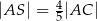 , to pole trójkąta
, to pole trójkąta 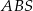 jest 16 razy większe od pola trójkąta
jest 16 razy większe od pola trójkąta 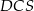 .
. 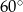 i
i 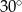 , a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
, a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw. 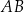 jest dłuższą podstawą trapezu równoramiennego
jest dłuższą podstawą trapezu równoramiennego 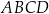 opisanego na okręgu o środku
opisanego na okręgu o środku 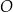 . Oblicz pole tego trapezu jeżeli
. Oblicz pole tego trapezu jeżeli 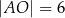 i
i 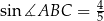 .
. 