Prosta 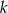 przechodząca przez punkt przecięcia przekątnych trapezu
przechodząca przez punkt przecięcia przekątnych trapezu 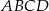 przecina jego podstawy
przecina jego podstawy 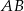 i
i 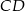 odpowiednio w punktach
odpowiednio w punktach 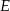 i
i 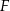 . Wykaż, że
. Wykaż, że 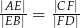 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez
Na trapezie opisano okrąg o promieniu długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc że przekątna tego trapezu ma długość 40 cm, oblicz obwód tego trapezu.
Ramię trapezu równoramiennego ma długość 12 cm. Kąt ostry tego trapezu ma miarę dwa razy mniejszą niż kąt rozwarty, a przekątna trapezu jest prostopadła do ramienia. Oblicz pole trapezu.
Ramię trapezu równoramiennego ma długość 18 cm. Kąt rozwarty tego trapezu ma miarę dwa razy większą niż kąt ostry, a przekątna trapezu jest prostopadła do ramienia. Oblicz pole trapezu.
W trapezie równoramiennym 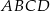 dłuższa podstawa
dłuższa podstawa 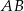 ma taką samą długość jak jego przekątna
ma taką samą długość jak jego przekątna 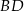 , a długość krótszej podstawy
, a długość krótszej podstawy 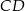 jest równa wysokości trapezu. Oblicz w jakim stosunku dzielą się przekątne tego trapezu.
jest równa wysokości trapezu. Oblicz w jakim stosunku dzielą się przekątne tego trapezu.
Trapez, w którym jedna z podstaw jest dwa razy dłuższa od drugiej, podzielono odcinkiem łączącym środki ramion trapezu na dwa czworokąty. Oblicz stosunek pól otrzymanych czworokątów.
Podstawy trapezu 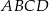 mają długości
mają długości 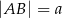 i
i 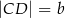 , przy czym
, przy czym 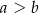 . Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość
. Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość 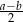 .
.
Przekątna trapezu równoramiennego dzieli jego kąt ostry na kąty o miarach  i
i 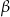 (
( – kąt między przekątną i podstawą). Wyznacz stosunek pól trójkątów, na jakie przekątna ta podzieliła trapez.
– kąt między przekątną i podstawą). Wyznacz stosunek pól trójkątów, na jakie przekątna ta podzieliła trapez.
W trapezie 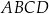 punkt
punkt 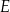 jest środkiem boku
jest środkiem boku 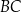 oraz
oraz 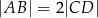 . Z wierzchołka
. Z wierzchołka 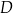 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 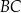 w punkcie
w punkcie 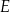 . Proste
. Proste 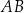 i
i 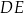 przecinają się w punkcie
przecinają się w punkcie 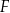 (zobacz rysunek).
(zobacz rysunek).
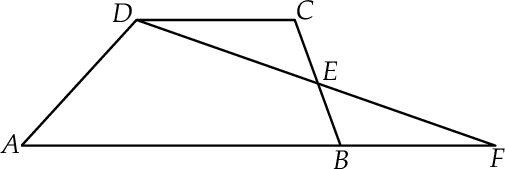
Wykaż, pole trójkąta 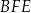 jest pięć razy mniejsze od pola czworokąta
jest pięć razy mniejsze od pola czworokąta 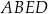 .
.
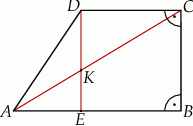
W trapezie prostokątnym 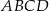 (rysunek) punkt
(rysunek) punkt 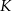 jest punktem przecięcia wysokości
jest punktem przecięcia wysokości 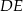 i przekątnej
i przekątnej 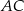 tego trapezu. Wiedząc, że
tego trapezu. Wiedząc, że 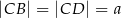 i
i 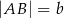 wykaż, że pole
wykaż, że pole 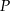 czworokąta
czworokąta 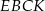 jest równe
jest równe 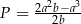 .
.
W trapezie opisanym na okręgu kąty przy dłuższej podstawie mają miary 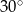 i
i 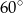 , a długość wysokości tego trapezu jest równa 6. Sporządź odpowiedni rysunek i oznacz jego elementy. Oblicz pole trapezu oraz długości jego podstaw.
, a długość wysokości tego trapezu jest równa 6. Sporządź odpowiedni rysunek i oznacz jego elementy. Oblicz pole trapezu oraz długości jego podstaw.
Podstawy trapezu równoramiennego mają długości  i
i 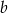 , gdzie
, gdzie 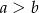 . Z wierzchołka kąta rozwartego trapezu poprowadzono wysokość. Uzasadnij, że wysokość ta dzieli dłuższą podstawę na odcinki o długościach
. Z wierzchołka kąta rozwartego trapezu poprowadzono wysokość. Uzasadnij, że wysokość ta dzieli dłuższą podstawę na odcinki o długościach 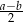 i
i 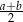 .
.
W trapez prostokątny 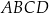 wpisano okrąg, przy czym punkt
wpisano okrąg, przy czym punkt 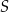 jest środkiem tego okręgu, a punkt
jest środkiem tego okręgu, a punkt 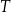 jest punktem styczności okręgu wpisanego z dłuższym ramieniem
jest punktem styczności okręgu wpisanego z dłuższym ramieniem 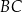 . Oblicz pole tego trapezu, jeśli
. Oblicz pole tego trapezu, jeśli 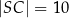 i
i 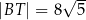 .
.

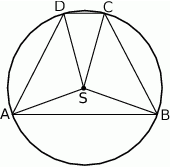
Punkt 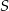 jest środkiem okręgu opisanego na trapezie równoramiennym
jest środkiem okręgu opisanego na trapezie równoramiennym 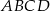 . Kąt
. Kąt 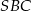 jest dwa razy większy od kąta
jest dwa razy większy od kąta 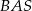 , a kąt
, a kąt 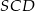 jest dwa razy większy od kąta
jest dwa razy większy od kąta 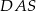 . Oblicz kąty trapezu
. Oblicz kąty trapezu 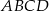 .
.
Trapez równoramienny 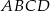 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Przekątna trapezu tworzy z dłuższą podstawą kąt
. Przekątna trapezu tworzy z dłuższą podstawą kąt  . Wyznacz obwód tego trapezu.
. Wyznacz obwód tego trapezu.
Podstawy trapezu mają długości 9 i 12. Oblicz długość odcinka łączącego środki przekątnych tego trapezu.
Na okręgu o danym promieniu  opisano trapez równoramienny
opisano trapez równoramienny 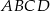 o dłuższej podstawie
o dłuższej podstawie 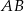 i krótszej
i krótszej 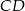 . Punkt styczności
. Punkt styczności 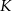 dzieli ramię
dzieli ramię 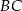 tak, że
tak, że 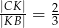 .
.
- Wyznacz długość ramienia tego trapezu.
- Oblicz cosinus kąta
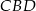 .
.
Trapez prostokątny 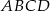 o podstawach
o podstawach 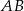 i
i 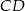 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  .
.
- Wykaż, że
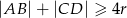 .
. - Wiedząc, że pole trapezu jest równe 4 wykaż, że
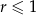 .
.
Dany jest trapez równoramienny 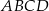 o obwodzie
o obwodzie 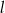 i podstawach
i podstawach 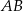 oraz
oraz 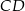 takich, że
takich, że 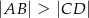 . Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna
. Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna 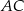 trapezu ma długość
trapezu ma długość 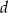 (zobacz rysunek).
(zobacz rysunek).
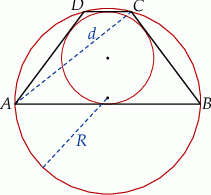
Wykaż, że promień 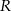 okręgu opisanego na trapezie
okręgu opisanego na trapezie 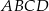 jest równy
jest równy 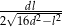 .
.
Ramiona trapezu prostokątnego mają długości 6 i 10. Odcinek łączący środki ramion ma długość 10. Oblicz długości podstaw trapezu.
Krótsza przekątna trapezu prostokątnego dzieli trapez na dwa trójkąty, z których jeden jest równoboczny. Znajdź pole tego trapezu wiedząc, że ramię prostopadłe do podstaw ma długość 2.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz pole tego trapezu.

