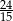W torebce jest mniej niż 100 cukierków. Ile ich jest jeżeli wiadomo, że można je podzielić na 5 równych części, można je podzielić też na 6 równych części, natomiast gdyby je podzielić na 7 części, to w jednej z nich będzie o 3 cukierki mniej od każdej z pozostałych.
/Szkoła podstawowa
Bok 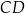 kwadratu
kwadratu 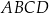 podzielono punktami
podzielono punktami 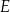 i
i 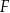 na trzy odcinki równej długości. Przez wierzchołek
na trzy odcinki równej długości. Przez wierzchołek 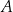 kwadratu i przez punkt
kwadratu i przez punkt 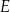 poprowadzono prostą (zobacz rysunek). Pole trójkąta
poprowadzono prostą (zobacz rysunek). Pole trójkąta 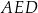 jest równe
jest równe 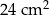 .
.
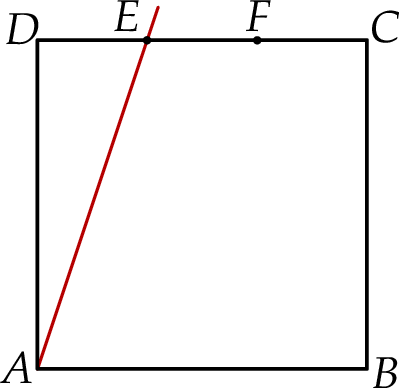
Oblicz pole kwadratu  .
.
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
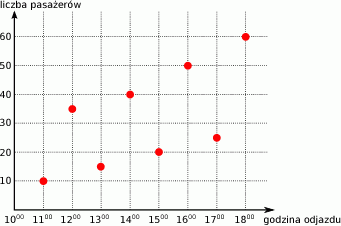
Ilu pasażerów jechało autobusem o godzinie 16:00?
A) 20 B) 40 C) 50 D) 60
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
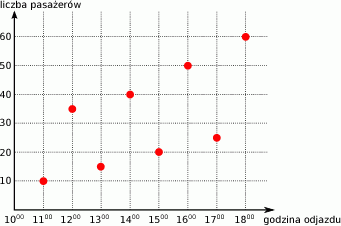
O której godzinie w autobusie było 35 pasażerów?
A) o 12:00 B) o 14:00 C) o 17:00 D) o żadnej
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
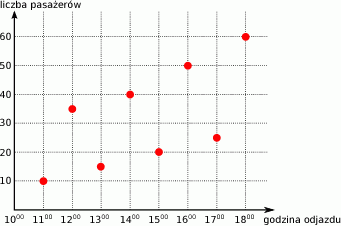
O ilu więcej pasażerów jechało o 17:00 niż o 13:00?
A) o 5 B) o 10 C) o 20 D) o 15
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
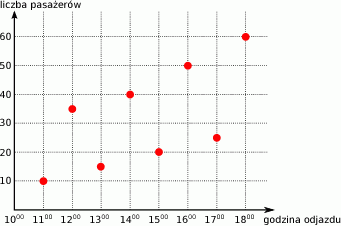
Ile razy więcej pasażerów jechało autobusem o 14:00, niż o 11:00?
A) 30 razy B) 4 razy C) 3 razy D) nie można tego obliczyć
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 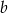 . O ile procent liczba
. O ile procent liczba 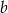 jest większa od liczby
jest większa od liczby  ?
?
A) 25% B) 80% C) 20% D) 120%
Jeżeli liczba  stanowi 40% dodatniej liczby
stanowi 40% dodatniej liczby 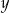 , to liczba
, to liczba 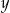 jest większa od liczby
jest większa od liczby  o:
o:
A) 60% B) 150% C) 160% D) 180%
Liczba 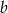 stanowi 40% liczby
stanowi 40% liczby  . O ile procent liczba
. O ile procent liczba  jest większa od liczby
jest większa od liczby 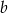 ?
?
A) 25% B) 60% C) 250% D) 150%
Liczba  stanowi 125% liczby
stanowi 125% liczby 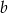 . O ile procent liczba
. O ile procent liczba 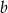 jest mniejsza od liczby
jest mniejsza od liczby  ?
?
A) 25% B) 80% C) 20% D) 120%
Liczba  stanowi 80% liczby dodatniej
stanowi 80% liczby dodatniej 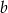 . Zatem liczba
. Zatem liczba 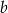 jest większa od liczby
jest większa od liczby  o:
o:
A) 15% B) 20% C) 25% D) 30%
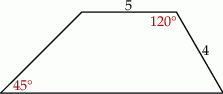
Oblicz pole i obwód trapezu przedstawionego na rysunku.
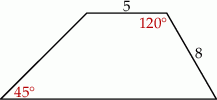
Oblicz pole i obwód trapezu przedstawionego na rysunku.
Koszt ubezpieczenia samochodu w pewnej firmie ubezpieczeniowej jest związany z wiekiem samochodu i polega na tym, że od ceny bazowej ubezpieczenia klient otrzymuje tyle procent zniżki, ile samochód ma lat.
Cena bazowa ubezpieczenia samochodu pana Jacka wynosi 620 zł. Ile zapłaci za to ubezpieczenie pan Jacek, jeżeli jego samochód ma 15 lat?
A) 93 zł B) 527 zł C) 605 zł D) 610 zł
Koszt ubezpieczenia samochodu w pewnej firmie ubezpieczeniowej jest związany z wiekiem samochodu i polega na tym, że od ceny bazowej ubezpieczenia klient otrzymuje tyle procent zniżki, ile samochód ma lat.
Cena bazowa ubezpieczenia samochodu Pani Uli wynosi 650 zł, ale Pani Ula za ubezpieczenie zapłaciła 598 zł. Ile lat ma samochód Pani Uli?
A) 52 B) 12 C) 8 D) 9
W koszu były 203 jednakowe sześcienne klocki. Zbudowano z nich możliwie największy sześcian, a pozostałe odłożono. Ile klocków odłożono?
A) 150 B) 125 C) 78 D) 53
W koszu były 303 jednakowe sześcienne klocki. Zbudowano z nich możliwie największy sześcian, a pozostałe odłożono. Ile klocków odłożono?
A) 87 B) 125 C) 178 D) 216
W pudełku znajdowały się piłeczki białe i czarne. Wśród wszystkich piłeczek 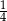 stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Kamil – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kamila piłeczki czarnej wynosi
stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Kamil – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kamila piłeczki czarnej wynosi 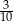 . Liczba wszystkich piłeczek czarnych, które początkowo znajdowały się w pudełku jest równa
. Liczba wszystkich piłeczek czarnych, które początkowo znajdowały się w pudełku jest równa
A) 18 B) 36 C) 24 D) 30
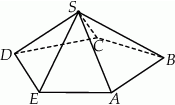
Dany jest ostrosłup o podstawie pięciokątnej  (zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta  . Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
. Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
Liczba 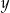 to 120% liczby
to 120% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 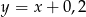 B)
B) 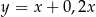 C)
C) 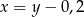 D)
D) 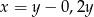
Liczba  stanowi 20% liczby
stanowi 20% liczby 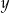 . Zatem prawdziwe jest następujące równanie
. Zatem prawdziwe jest następujące równanie
A) 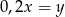 B)
B) 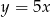 C)
C) 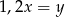 D)
D) 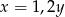
Dodatnia liczba  stanowi 30% liczby
stanowi 30% liczby 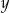 . Wówczas
. Wówczas
A) 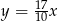 B)
B) 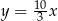 C)
C) 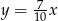 D)
D) 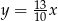
Liczba 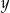 to 140% liczby
to 140% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 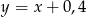 B)
B) 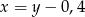 C)
C) 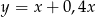 D)
D) 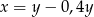
Liczba  jest o 30% większa od liczby
jest o 30% większa od liczby 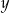 . Z tego wynika, że
. Z tego wynika, że
A) 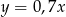 B)
B) 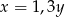 C)
C) 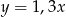 D)
D) 
Dodatnia liczba  stanowi 70% liczby
stanowi 70% liczby 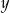 . Wówczas
. Wówczas
A) 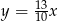 B)
B) 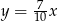 C)
C) 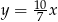 D)
D) 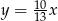
Liczba 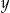 jest o 30% większa od liczby
jest o 30% większa od liczby  . Z tego wynika, że
. Z tego wynika, że
A) 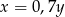 B)
B) 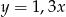 C)
C) 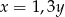 D)
D) 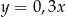
Liczba  stanowi 60% liczby
stanowi 60% liczby 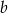 . Wówczas:
. Wówczas:
A) 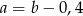 B)
B) 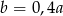 C)
C) 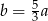 D)
D) 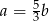
Liczba  jest o 30% mniejsza od liczby
jest o 30% mniejsza od liczby 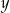 . Z tego wynika, że
. Z tego wynika, że
A) 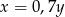 B)
B) 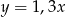 C)
C) 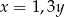 D)
D) 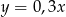
W kwadracie o boku 6 narysowano dwie ćwiartki okręgu o promieniu 6 (patrz rysunek).
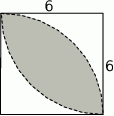
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole zacieniowanej figury jest równe 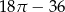 | P | F |
| Obwód zacieniowanej figury jest mniejszy od 21. | P | F |
Funkcja dana jest za pomocą grafu.
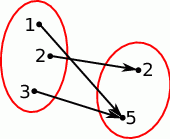
- Jakie są argumenty tej funkcji?
- Jakie są wartości tej funkcji?
- Jaką wartość przyjmuje ta funkcja dla argumentu 2?
- Dla jakich argumentów funkcja przyjmuje wartość 5?
Listewkę o długości 50 cm planowano pociąć na równe części. Iwona zaproponowała podział na kawałki po 5 cm i zaznaczyła na listewce czerwonym kolorem linie cięcia. Agata chciała podzielić tę samą listewkę na części po 2 cm i linie cięcia zaznaczyła na zielono. Ile razy linia czerwona pokrywała się z linią zieloną?
A) 5 B) 4 C) 3 D) 2
Listewkę o długości 60 cm planowano pociąć na równe części. Iwona zaproponowała podział na kawałki po 5 cm i zaznaczyła na listewce czerwonym kolorem linie cięcia. Agata chciała podzielić tę samą listewkę na części po 2 cm i linie cięcia zaznaczyła na zielono. Ile razy linia czerwona pokrywała się z linią zieloną?
A) 5 B) 4 C) 3 D) 2
Drewniany sześcian rozcięto na identyczne mniejsze sześciany, a następnie usunięto część z nich tworząc trzy puste tunele łączące przeciwległe ściany (zobacz rysunek). Otrzymana w ten sposób bryła została w całości zanurzona w niebieskiej farbie.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Otrzymana bryła składa się ze 110 małych sześcianów. | P | F |
| 24 małe sześciany mają dokładnie jedną ścianę pomalowaną na niebiesko. | P | F |
W tabelce podano pola kwadratów. Ustal, które z nich mają boki o długościach wyrażonych liczbami całkowitymi.
 | 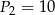 |
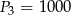 | 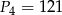 |
W tabelce podano pola kwadratów. Ustal, które z nich mają boki o długościach wyrażonych liczbami wymiernymi.
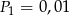 | 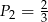 |
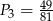 | 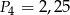 |
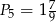 | 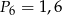 |
Punkt 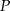 jest punktem wspólnym symetralnych boków
jest punktem wspólnym symetralnych boków 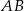 i
i 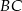 trójkąta
trójkąta 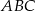 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Odległość punktu  od wierzchołków od wierzchołków  i i 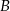 jest taka sama. jest taka sama. | P | F |
Odległość punktu 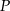 od wierzchołków od wierzchołków 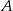 i i 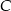 jest taka sama. jest taka sama. | P | F |
Kasia kupiła dwa i pół kilograma landrynek po 20 zł za kilogram, pół kilograma cukierków czekoladowych po 14 zł za kilogram i kilogram cukierków kawowych po 15 zł za kilogram. Średnia wartość 1 kg cukierków, które kupiła Kasia, była równa
A) 18 zł B) ok. 16,30 zł C) 24 zł D) 23 zł
Ewa kupiła trzy i pół kilograma landrynek po 16 zł za kilogram, dwa i pół kilograma cukierków czekoladowych po 12 zł za kilogram i dwa kilogramy cukierków kawowych po 11 zł za kilogram. Średnia wartość 1 kg cukierków, które kupiła Kasia, była równa
A) 13 zł B) 14 zł C) 13,5 zł D) 14,2 zł
Jacek kupił pół kilograma landrynek po 18 zł za kilogram, dwa i pół kilograma cukierków czekoladowych po 16 zł za kilogram i kilogram cukierków kawowych po 13 zł za kilogram. Średnia wartość 1 kg cukierków, które kupił Jacek, była równa
A) 15,50 zł B) 16,30 zł C) 23,50 zł D) 17,20 zł
Na przedstawionym poniżej fragmencie osi liczbowej oznaczono cztery punkty: 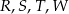 . Współrzędne punktów
. Współrzędne punktów 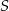 i
i 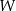 są równe 287 i 311. Odcinek
są równe 287 i 311. Odcinek 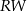 jest podzielony na pięć równych części.
jest podzielony na pięć równych części.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Współrzędne punktów 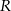 i i 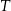 różnią się o 24. różnią się o 24. | P | F |
Współrzędna punktu 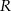 jest równa 271. jest równa 271. | P | F |
Na przedstawionym poniżej fragmencie osi liczbowej oznaczono cztery punkty: 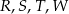 . Współrzędne punktów
. Współrzędne punktów 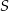 i
i 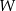 są równe 283 i 419. Odcinek
są równe 283 i 419. Odcinek 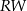 jest podzielony na sześć równych części.
jest podzielony na sześć równych części.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Współrzędne punktów 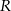 i i 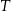 różnią się o 102. różnią się o 102. | P | F |
Współrzędna punktu 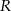 jest równa 215. jest równa 215. | P | F |
Na torze wyścigowym zorganizowano wyścig samochodowy, w którym wzięły udział dwa samochody. Oba samochody wystartowały w tym samym momencie i każdy z nich pokonał dystans 600 km, przy czym do mety jako pierwszy przyjechał samochód nr 2. Wykresy przedstawiają zależność drogi przebytej przez oba samochody od czasu jazdy.
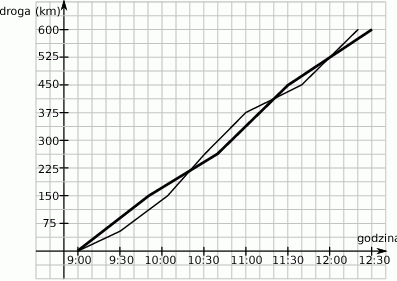
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po rozpoczęciu wyścigu trzykrotnie następowała zmiana lidera. | P | F |
| Gdyby wyścig zakończył się po 300 km, to wygrałby go samochód nr 1. | P | F |
Na torze wyścigowym zorganizowano wyścig samochodowy, w którym wzięły udział dwa samochody. Oba samochody wystartowały w tym samym momencie i każdy z nich pokonał dystans 600 km, przy czym do mety jako pierwszy przyjechał samochód nr 2. Wykresy przedstawiają zależność drogi przebytej przez oba samochody od czasu jazdy.
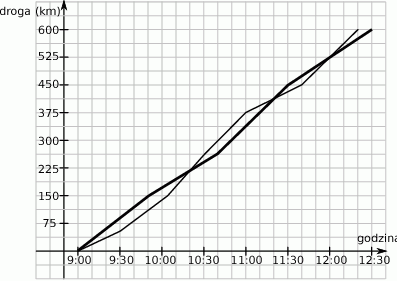
Średnia prędkość samochodu nr 2 na trasie wyścigu wyniosła
A) 150 km/h B) 171,4 km/h C) 180 km/h D) 190 km/h
Rozwinięcie dziesiętne nieskończone ma liczba
A) 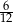 B)
B) 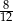 C)
C) 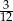 D)
D) 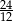
Rozwinięcie dziesiętne nieskończone ma liczba
A) 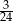 B)
B) 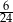 C)
C) 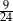 D)
D) 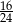
Rozwinięcie dziesiętne nieskończone ma liczba
A) 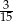 B)
B) 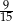 C)
C) 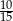 D)
D)