Rzeka Wisła ma długość 1047 km,
- Zaokrąglij tę wielkość do pełnych setek km.
- Oblicz błąd względny otrzymanego przybliżenia z dokładnością do 0,1%.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rzeka Wisła ma długość 1047 km,
W pewnym liceum 85% uczniów posiada telefony komórkowe. Pozostałych 27 uczniów nie posiada telefonów komórkowych. Wobec tego telefony posiada
A) mniej niż 160 osób B) więcej niż 200 osób C) 180 osób D) 154 osoby
W pewnej szkole 75% uczniów mieszka w internacie. Pozostałych 105 uczniów dojeżdża do szkoły autobusem. Wobec tego w internacie mieszka
A) mniej niż 300 uczniów B) więcej niż 400 uczniów C) 315 uczniów D) 210 uczniów.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 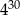 jest 128 razy większa od liczby jest 128 razy większa od liczby 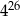 . . | P | F |
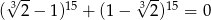 | P | F |
Wiadomo, że 8% pewnej liczby jest równe 10. Zatem 10% tej liczby wynosi
A) 12,5 B) 15 C) 18 D) 8
Wiadomo, że 8% pewnej liczby jest równe 10. Zatem 12% tej liczby wynosi
A) 12,5 B) 15 C) 18 D) 8
Wiadomo, że 9% pewnej liczby jest równe 16,2. Zatem 10% tej liczby wynosi
A) 12,5 B) 15 C) 18 D) 8
6% pewnej liczby jest równe 15. 14% tej liczby jest równe
A) 28 B) 36 C) 32 D) 35
Jeśli, 120% pewnej liczby jest równe 480, to 75% tej liczby jest równe
A) 250 B) 300 C) 350 D) 400
Liczba 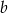 to 125% liczby
to 125% liczby  . Wskaż zdanie fałszywe.
. Wskaż zdanie fałszywe.
A) 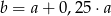 B)
B) 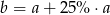 C)
C) 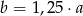 D)
D) 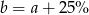
Liczba 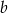 to 95% liczby
to 95% liczby  . Wskaż zdanie fałszywe.
. Wskaż zdanie fałszywe.
A) 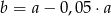 B)
B) 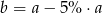 C)
C) 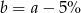 D)
D) 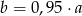
W trójkącie 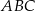 narysowano dwie wysokości:
narysowano dwie wysokości: 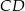 i
i 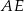 , jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy
, jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy 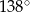 .
.
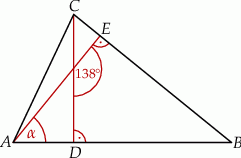
Jaką miarę ma kąt  zaznaczony na rysunku?
zaznaczony na rysunku?
A) 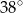 B)
B) 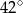 C)
C) 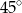 D)
D) 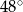
W trójkącie 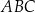 narysowano dwie wysokości:
narysowano dwie wysokości: 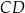 i
i 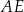 , jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy
, jak na rysunku. Kąt rozwarty pomiędzy tymi wysokościami jest równy 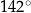 .
.
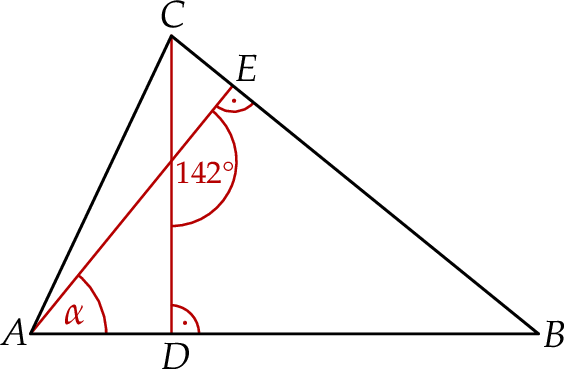
Jaką miarę ma kąt  zaznaczony na rysunku?
zaznaczony na rysunku?
A) 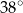 B)
B) 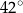 C)
C) 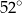 D)
D) 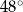
Na rysunku przedstawiono schemat budowy muru z cegieł oraz dwa przykładowe mury: jeden o szerokości 5 i wysokości 3 cegieł oraz drugi o szerokości 6 i wysokości 5 cegieł.

Do zbudowania muru o szerokości  i wysokości 11 cegieł potrzeba
i wysokości 11 cegieł potrzeba
A) 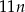 cegieł. B)
cegieł. B) 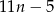 cegieł. C)
cegieł. C) 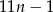 cegieł. D)
cegieł. D) 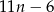 cegieł.
cegieł.
Na rysunku przedstawiono schemat budowy muru z cegieł oraz dwa przykładowe mury: jeden o szerokości 5 i wysokości 3 cegieł oraz drugi o szerokości 6 i wysokości 5 cegieł.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli zwiększamy szerokość muru dwukrotnie, to liczba cegieł potrzebnych do jego budowy również rośnie dwukrotnie. | P | F |
| W każdym ze zbudowanych w ten sposób murów liczba cegieł jest liczbą parzystą. | P | F |
Okrąg wpisany w czworokąt 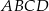 ma środek
ma środek 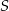 i jest styczny do boków
i jest styczny do boków 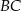 i
i 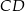 odpowiednio w punktach
odpowiednio w punktach 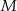 i
i 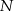 . Kąt
. Kąt 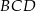 ma miarę
ma miarę 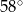 (rysunek).
(rysunek).
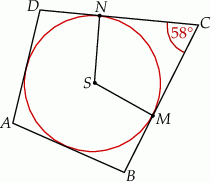
Kąt 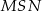 ma miarę
ma miarę
A) 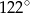 B)
B) 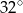 C)
C) 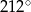 D)
D) 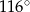
Wierzchołek 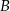 równoległoboku
równoległoboku 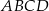 ma współrzędne
ma współrzędne
A) 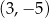 B)
B) 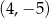 C)
C) 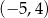 D)
D) 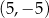
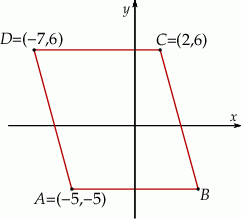
Na rysunku przedstawiono równoległobok 
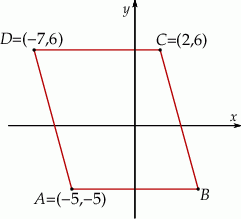
Pole równoległoboku  jest równe A/B.
jest równe A/B.
A) 99 B) 80
Wierzchołek  równoległoboku
równoległoboku  ma współrzędne C/D.
ma współrzędne C/D.
C) 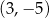 D)
D) 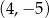
Wykaż, że liczba 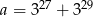 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że liczba 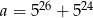 jest podzielna przez 130.
jest podzielna przez 130.
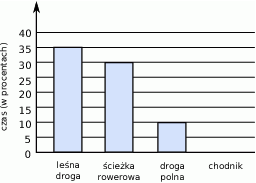
Asia jeździła rowerem 2 godziny. Na diagramie przedstawiono w procentach (w %) czas jazdy Asi po leśnej drodze, ścieżce rowerowej i polnej drodze, ale nie narysowano słupka z informacją o czasie jazdy po chodniku.
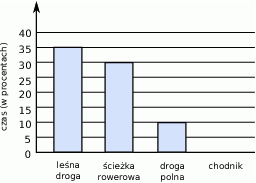
Asia jeździła rowerem 2 godziny. Na diagramie przedstawiono w procentach (w %) czas jazdy Asi po leśnej drodze, ścieżce rowerowej i polnej drodze, ale nie narysowano słupka z informacją o czasie jazdy po chodniku.
Na giełdzie kupiono tę samą liczbę akcji dwóch przedsiębiorstw, przy czym średnia cena zakupu jednej akcji drugiego przedsiębiorstwa była dwa razy wyższa od średniej ceny akcji pierwszego przedsiębiorstwa. Ile średnio zapłacono za jedną akcję drugiego przedsiębiorstwa, jeżeli średnia cena zakupu wszystkich akcji wyniosła 90 zł?
A) 30 zł B) 60 zł C) 90 zł D) 120 zł
Właściciel salonu samochodowego sporządził diagram, na którym zaznaczył miesięczną sprzedaż samochodów w okresie styczeń 2017 – grudzień 2018.
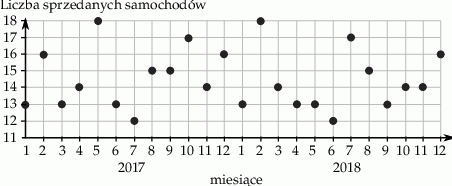
W którym z podanych okresów sprzedano najmniejszą liczbę samochodów?
A) styczeń 2017 – czerwiec 2017 B) lipiec 2017 – grudzień 2017
C) styczeń 2018 – czerwiec 2018 D) lipiec 2018 – grudzień 2018
Właściciel salonu samochodowego sporządził diagram, na którym zaznaczył miesięczną sprzedaż samochodów w okresie styczeń 2017 – grudzień 2018.
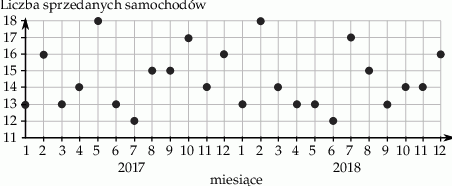
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Łączna sprzedaż samochodów w dwóch kolejnych miesiącach nigdy nie przekroczyła 32 sztuk. | P | F |
| Liczba miesięcy, w których sprzedaż przekroczyła 15 samochodów była większa niż liczba miesięcy, w których sprzedaż była mniejsza niż 15 samochodów. | P | F |
Z reguł działań na potęgach wynika, że:
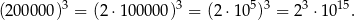
Z tych samych reguł wynika, że liczba 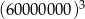 jest równa
jest równa
A) 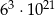 B)
B) 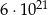 C)
C) 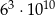 D)
D) 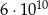
Z reguł działań na potęgach wynika, że:
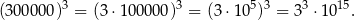
Z tych samych reguł wynika, że liczba 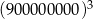 jest równa
jest równa
A) 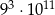 B)
B) 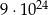 C)
C) 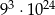 D)
D) 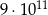
W zalanej kopalni zainstalowano 3 pompy wypompowujące wodę z zalanych sztolni. Pierwsza pompa pracująca sama wypompowałaby wodę w ciągu 12 dni, druga w ciągu 15 dni, a trzecia 20 dni. Pierwsze trzy dni pierwsza i trzecia pompa pracowały wspólnie. Następnie włączono dodatkowo drugą pompę. Jak długo trwało wypompowywanie wody z kopalni?
Wiadomo, że mediana liczb 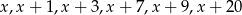 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 5 B) 26 C) 28 D) 4
Wiadomo, że mediana liczb 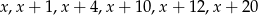 jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 4 B) 28 C) 22 D) 24
Wiadomo, że mediana liczb 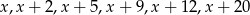 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 2 B) 16 C) 22 D) 24
Jaka jest miara kąta  ?
?
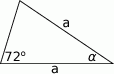
Jaka jest miara kąta  ?
?
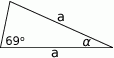
Jaka jest miara kąta  ?
?
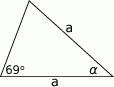
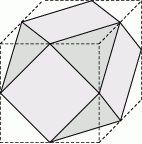
W kostce mającej kształt sześcianu o krawędzi długości 6 ścięto wszystkie naroża płaszczyznami przechodzącymi przez środki odpowiednich krawędzi (zobacz rysunek). Oblicz objętość otrzymanej bryły.
Poniżej przedstawiono składniki potrzebne do przygotowania ciasta na 8 gofrów.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Do przygotowania ciasta na 40 gofrów, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 10 jajek. | P | F |
| Do przygotowania ciasta na 72 gofry, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 12 szklanek mleka. | P | F |
Poniżej przedstawiono składniki potrzebne do przygotowania ciasta na 15 racuchów.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Do przygotowania ciasta na 40 racuchów, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 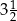 szklanki mąki. szklanki mąki. | P | F |
Do przygotowania ciasta na 54 racuchy, przy zachowaniu właściwych proporcji odpowiednich składników, potrzeba 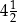 szklanki mleka. szklanki mleka. | P | F |
Poniżej przedstawiono listę produktów, z których przygotowano 8 identycznych paczek świątecznych.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Do przygotowania kolejnych 17 paczek świątecznych, o takiej samej zawartości jak pierwsze 8 paczek, potrzeba ponad 6 kg suszonych owoców. | P | F |
| Gdyby przygotować 73 paczki świąteczne, o takiej samej zawartości jak 8 paczek opisanych w treści zadania, to w tych 73 paczkach liczba pierniczków byłaby równa sumie liczby mandarynek i liczby lizaków. | P | F |
Rozwiąż równanie: 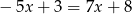 .
.
Rozwiąż równanie: 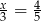 .
.
Rozwiąż równanie: 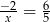 .
.
Rozwiąż równanie: 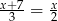 .
.
Rozwiąż równanie: 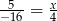 .
.
