Jeżeli trzecia część liczby przeciwnej do odwrotności sześcianu pewnej liczby jest równa 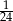 , to ta liczba jest równa
, to ta liczba jest równa
A) 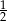 B) 2 C)
B) 2 C) 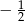 D)
D) 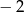
/Szkoła podstawowa
Dane są trzy wyrażenia:
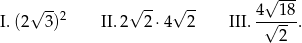
Wartości których wyrażeń są mniejsze od 15?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
Dane są trzy wyrażenia:
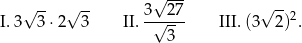
Wartości których wyrażeń są większe od 6?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
Dany jest trójkąt 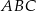 , w którym kąt
, w którym kąt 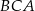 ma miarę
ma miarę 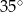 . Punkt
. Punkt 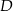 leży na boku
leży na boku 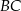 tego trójkąta. Odcinek
tego trójkąta. Odcinek 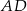 ma taką samą długość jak odcinek
ma taką samą długość jak odcinek 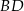 . Kąt
. Kąt 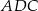 ma miarę
ma miarę 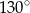 (zobacz rysunek poniżej).
(zobacz rysunek poniżej).
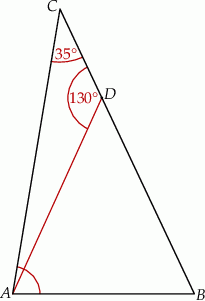
Kąt 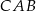 ma miarę
ma miarę
A) 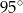 B)
B) 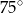 C)
C) 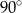 D)
D) 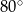
Dany jest trójkąt 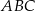 , w którym kąt
, w którym kąt 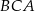 ma miarę
ma miarę 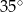 . Punkt
. Punkt 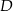 leży na boku
leży na boku 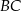 tego trójkąta. Odcinek
tego trójkąta. Odcinek 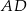 ma taką samą długość jak odcinek
ma taką samą długość jak odcinek 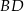 . Kąt
. Kąt 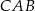 ma miarę
ma miarę 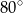 (zobacz rysunek poniżej).
(zobacz rysunek poniżej).
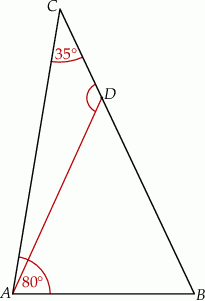
Kąt 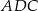 ma miarę
ma miarę
A) 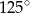 B)
B) 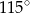 C)
C) 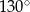 D)
D) 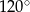
Narysowana poniżej figura składa się z kwadratu o boku 2 i trzech ćwiartek koła.
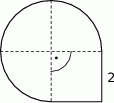
Obwód tej figury jest równy
A) 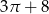 B)
B) 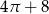 C)
C) 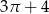 D)
D) 
Narysowana poniżej figura składa się z dwóch kwadratów o boku 2 i dwóch ćwiartek koła.
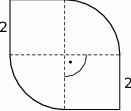
Obwód tej figury jest równy
A) 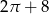 B)
B) 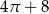 C)
C) 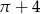 D)
D) 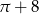
Z kartki w kształcie kwadratu o boku 6 odcięto ćwierć koła o promieniu 6 (patrz rysunek).
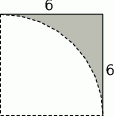
Pole powierzchni pozostałej zacieniowanej części kartki jest równe
A) 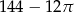 B)
B) 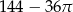 C)
C) 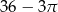 D)
D) 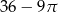
Na rysunku przedstawiono trapez równoramienny o podstawach 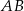 i
i 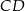 . Dane są długości odcinków
. Dane są długości odcinków 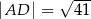 ,
, 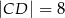 ,
, 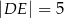 .
.
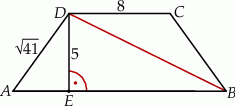
Długość przekątnej 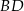 jest równa
jest równa
A) 13 B) 14 C) 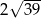 D)
D) 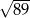
Paweł wyciął z kartonu trójkąt prostokątny  o przyprostokątnych 12 cm i 16 cm (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
o przyprostokątnych 12 cm i 16 cm (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt  wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez  (rysunek II).
(rysunek II).
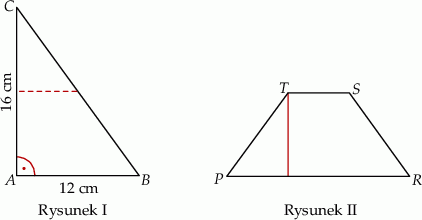
Oblicz różnicę obwodów trójkąta 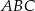 i trapezu
i trapezu 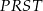 .
.
Karol wyciął z kartonu trójkąt prostokątny 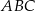 (rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt
(rysunek I). Następnie połączył środki dłuższej przyprostokątnej i przeciwprostokątnej linią przerywaną równoległą do krótszej przyprostokątnej, a potem rozciął trójkąt 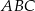 wzdłuż tej linii na dwie figury. Z tych figur złożył trapez
wzdłuż tej linii na dwie figury. Z tych figur złożył trapez 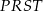 o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
o krótszej podstawie długości 9 cm i ramieniu długości 15 cm (rysunek II).
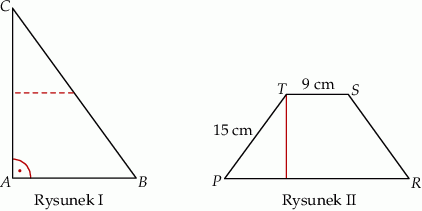
Oblicz różnicę obwodów trójkąta 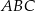 i trapezu
i trapezu 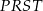 .
.
Dane są liczby: 12195, 43176, 54145, 57492, 61020, 37170.
Wśród danych liczb są dokładnie A/B liczby podzielne przez 12.
A) trzy B) cztery
Wśród danych liczb są dokładnie C/D liczby podzielne przez 45.
C) dwie D) trzy
Dwa sześciany – jeden o krawędzi 2 i drugi o krawędzi 3 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 35 B) 47 C) 94 D) 142
Dwa sześciany – jeden o krawędzi 3 i drugi o krawędzi 4 – pocięto na sześciany o krawędzi 1. Z otrzymanych sześcianów zbudowano prostopadłościan. Żadna ściana tego prostopadłościanu nie jest kwadratem. Pole powierzchni zbudowanego prostopadłościanu jest równe
A) 150 B) 222 C) 366 D) 111
W prostokątnym układzie współrzędnych przedstawiono wykres funkcji.
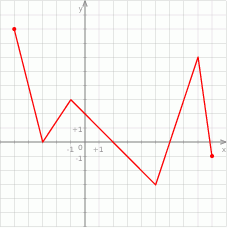
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja  dla argumentów ujemnych przyjmuje wartości dodatnie. dla argumentów ujemnych przyjmuje wartości dodatnie. | P | F |
Funkcja  pewną wartość przyjmuje dla 4 argumentów. pewną wartość przyjmuje dla 4 argumentów. | P | F |
Który z poniższych rysunków nie może być siatką ostrosłupa prawidłowego czworokątnego?
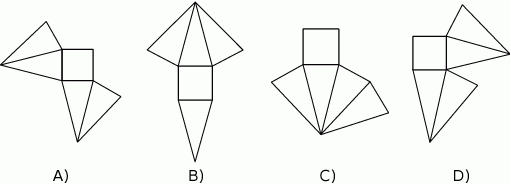
Maciek pływa w basenie o długości 25 m. W jednym końcu basenu głębokość wynosi 3 m, a w drugim 1,5 m. Kąt nachylenia dna basenu do powierzchni wody jest stały.
- Czy Maciek ’ma grunt’ pod stopami w odległości 10 m od płytszego końca basenu? Przyjmij, że wzrost Maćka wynosi 180 cm, a basen jest całkowicie wypełniony wodą.
- Oblicz pojemność basenu, w którym pływa Maciek. Szerokość basenu wynosi 10 m.
Na poniższym wykresie przedstawiono jak zmieniała się liczba ludności Europy i Afryki w latach 1950–2010 (wykresy mają różne osie pionowe).
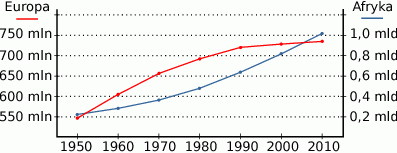
- Ile wynosiła liczba mieszkańców Europy, a ile Afryki w 1980 roku?
- Ile razy więcej osób mieszkało w Europie niż w Afryce w 1960 roku?
- W którym roku liczba mieszkańców Afryki przekroczyła liczbę mieszkańców Europy?
- O ile procent zwiększyła się liczba ludności Europy, a o ile Afryki w latach 1950–2010?
Liczba 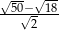 jest równa
jest równa
A) 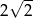 B) 2 C) 4 D)
B) 2 C) 4 D) 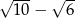
Liczba 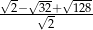 jest równa
jest równa
A) 7 B) 6 C) 5 D) 4
Iloraz 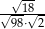 jest równy
jest równy
A)  B)
B) 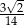 C)
C) 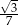 D)
D) 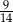
Iloraz 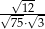 jest równy
jest równy
A) 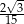 B)
B)  C)
C) 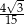 D)
D) 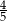
Liczba 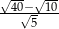 jest równa
jest równa
A) 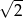 B)
B) 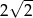 C) 4 D)
C) 4 D) 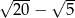
Liczba 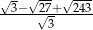 jest równa
jest równa
A) 5 B) 6 C) 7 D) 8
Która z podanych niżej liczb nie jest równa 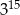 ?
?
A) 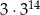 B)
B) 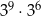 C)
C) 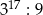 D)
D) 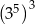 E)
E) 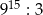
Która z podanych niżej liczb nie jest równa 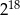 ?
?
A) 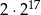 B)
B) 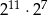 C)
C) 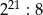 D)
D) 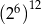 E)
E) 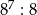
Oblicz 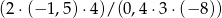 .
.
Wierzchołek 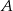 trójkąta ostrokątnego
trójkąta ostrokątnego 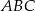 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 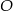 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 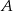 poprowadzono wysokość
poprowadzono wysokość 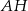 . Wykaż, że
. Wykaż, że 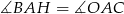 .
.
Korzystając z tego, że 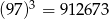 , wskaż wartość liczby
, wskaż wartość liczby 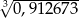 .
.
A) 0,0097 B) 0,097 C) 0,97 D) 9,7
W przedziale 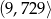 potęg liczby 3 jest
potęg liczby 3 jest
A) 6 B) 5 C) 4 D) 3
W przedziale 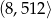 potęg liczby 2 jest
potęg liczby 2 jest
A) 6 B) 5 C) 4 D) 3
W przedziale 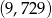 potęg liczby 3 jest
potęg liczby 3 jest
A) 6 B) 5 C) 4 D) 3
Na rysunku przedstawiono trzy figury: prostokąt, kwadrat, trójkąt.
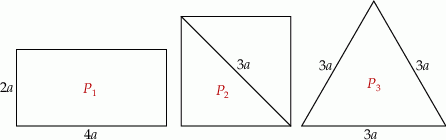
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Spośród przedstawionych figur największe pole ma figura 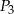 . . | P | F |
Spośród podanych figur najmniejsze pole ma figura  . . | P | F |
Siatka narysowanego graniastosłupa prostego składa się
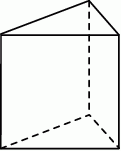
A) z 2 trójkątów i 2 prostokątów B) z 2 trójkątów i 3 prostokątów
C) z 3 trójkątów i 2 prostokątów D) z 3 trójkątów i 3 prostokątów

