W konkursie przyznano nagrody pieniężne. Zdobywca pierwszego miejsca otrzymał 5000 zł. Nagroda za zdobycie drugiego miejsca była o 30% mniejsza niż nagroda za zajęcie pierwszego miejsca. Nagroda za zdobycie trzeciego miejsca była o 40% mniejsza niż nagroda za zajęcie drugiego miejsca. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Uczestnik konkursu, który zdobył trzecie miejsce, otrzymał 1400 zł. | P | F |
| Nagroda za zdobycie trzeciego miejsca była o 70% mniejsza od nagrody za zajęcie pierwszego miejsca. | P | F |

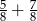 .
. 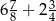 .
. 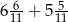 .
. 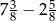 .
.  .
.  .
.  .
.  .
.  .
.  .
.  .
.  .
. 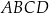 o polu
o polu 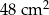 przekątna
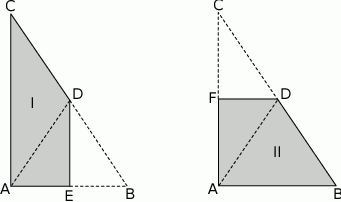
przekątna 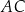 ma długość 8 cm i dzieli ten czworokąt na dwa trójkąty:
ma długość 8 cm i dzieli ten czworokąt na dwa trójkąty: 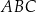 i
i 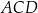 (zobacz rysunek). Wysokość trójkąta
(zobacz rysunek). Wysokość trójkąta 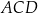 poprowadzona z wierzchołka
poprowadzona z wierzchołka 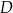 do prostej
do prostej 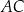 jest równa 2 cm.
jest równa 2 cm. 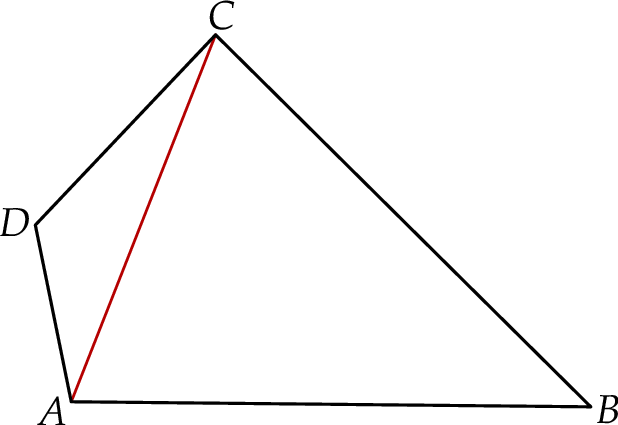
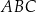 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka 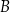 do prostej
do prostej 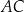 .
. 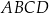 o polu
o polu 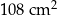 przekątna
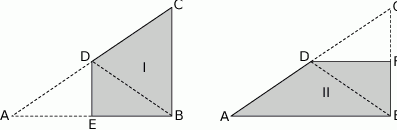
przekątna 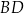 ma długość 12 cm i dzieli ten czworokąt na dwa trójkąty:
ma długość 12 cm i dzieli ten czworokąt na dwa trójkąty: 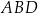 i
i 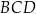 (zobacz rysunek). Wysokość trójkąta
(zobacz rysunek). Wysokość trójkąta 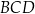 poprowadzona z wierzchołka
poprowadzona z wierzchołka 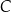 do prostej
do prostej 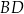 jest równa 3 cm.
jest równa 3 cm. 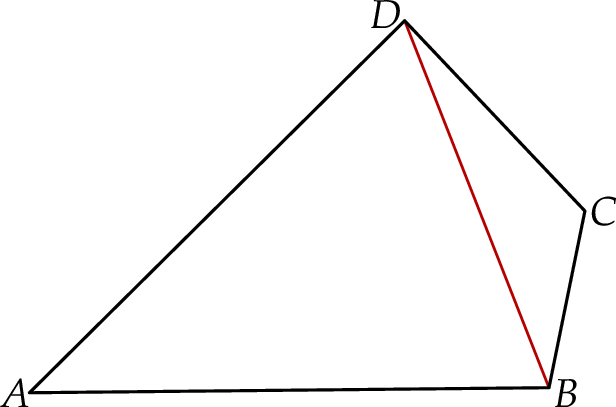
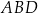 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka 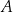 do prostej
do prostej 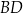 .
. 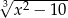 nie może być obliczone w zbiorze liczb rzeczywistych?
nie może być obliczone w zbiorze liczb rzeczywistych?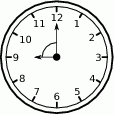
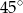
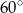
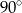
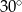
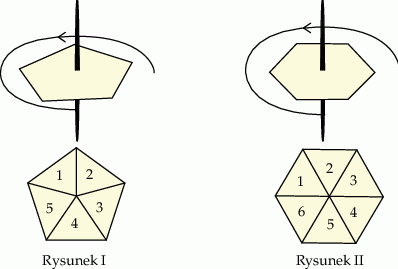
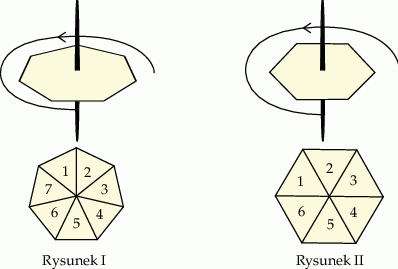
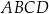 podzielono na 6 kwadratów: jeden duży, dwa średnie i trzy małe (zobacz rysunek).
podzielono na 6 kwadratów: jeden duży, dwa średnie i trzy małe (zobacz rysunek). 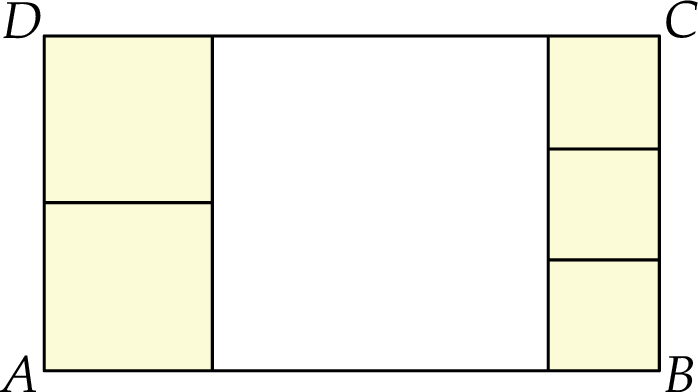
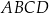 .
. 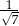 .
. 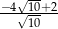 .
. 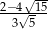 .
. 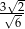 .
. 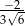 .
. 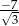 .
. 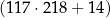 .
. funkcja przyjmuje wartości dodatnie, a dla jakich ujemne.
funkcja przyjmuje wartości dodatnie, a dla jakich ujemne. 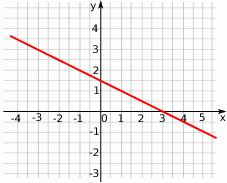
 funkcja przyjmuje wartości dodatnie, a dla jakich ujemne.
funkcja przyjmuje wartości dodatnie, a dla jakich ujemne. 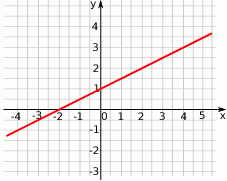
 funkcja przyjmuje wartości dodatnie, a dla jakich ujemne.
funkcja przyjmuje wartości dodatnie, a dla jakich ujemne. 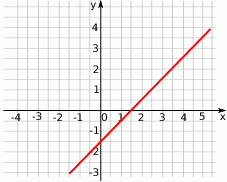
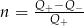 i
i 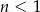 to
to 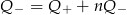
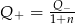
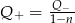
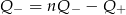
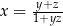 i
i 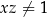 , to
, to 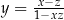
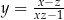
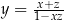
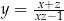
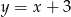 przyjmuje wartości dodatnie, a dla jakich ujemne.
przyjmuje wartości dodatnie, a dla jakich ujemne. 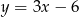 przyjmuje wartości dodatnie, a dla jakich ujemne.
przyjmuje wartości dodatnie, a dla jakich ujemne. 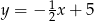 przyjmuje wartości dodatnie, a dla jakich ujemne.
przyjmuje wartości dodatnie, a dla jakich ujemne. 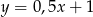 przyjmuje wartości dodatnie, a dla jakich ujemne.
przyjmuje wartości dodatnie, a dla jakich ujemne. 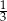 masy kupionej ziemi. W czerwcu zużył połowę masy ziemi, która została. Na lipiec pozostało mu jeszcze 60 kg ziemi. Jeżeli przez
masy kupionej ziemi. W czerwcu zużył połowę masy ziemi, która została. Na lipiec pozostało mu jeszcze 60 kg ziemi. Jeżeli przez  oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie
oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie 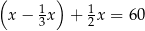
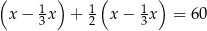
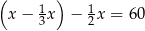
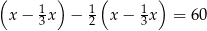
 masy kupionej ziemi. W czerwcu zużył
masy kupionej ziemi. W czerwcu zużył  masy ziemi, która została. Na lipiec pozostało mu jeszcze 50 kg ziemi. Jeżeli przez
masy ziemi, która została. Na lipiec pozostało mu jeszcze 50 kg ziemi. Jeżeli przez  oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie
oznaczymy masę zakupionej ziemi, to sytuację przedstawioną w zadaniu opisuje równanie 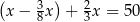
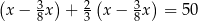
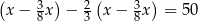
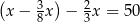
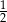
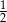
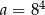 i
i 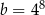 .
. 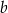 należy liczbę
należy liczbę  A/B.
A/B.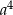 należy liczbę
należy liczbę 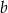 C/D.
C/D.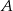 i
i 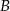 w ciągu 48 minut, a średnia prędkość piechura na tej samej trasie jest trzykrotnie mniejsza od średniej prędkości rowerzysty. O ile minut wcześniej niż rowerzysta piechur musi wyjść z miasta
w ciągu 48 minut, a średnia prędkość piechura na tej samej trasie jest trzykrotnie mniejsza od średniej prędkości rowerzysty. O ile minut wcześniej niż rowerzysta piechur musi wyjść z miasta 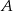 tak, aby obaj dotarli do miasta
tak, aby obaj dotarli do miasta 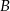 w tym samym momencie?
w tym samym momencie? 