Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| 120% liczby 180 to tyle samo, co 180% liczby 120. | P | F |
| 20% liczby 36 to tyle samo, co 40% liczby 18. | P | F |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| 120% liczby 180 to tyle samo, co 180% liczby 120. | P | F |
| 20% liczby 36 to tyle samo, co 40% liczby 18. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| 40% liczby 140 to tyle samo, co 140% liczby 40. | P | F |
| 30% liczby 42 to tyle samo, co 60% liczby 84. | P | F |
Średnie zużycie paliwa na pierwszym odcinku trasy było równe 7 litrów na 100 kilometrów, a średnie zużycie paliwa na drugim, dwa razy dłuższym odcinku trasy, było równe 10 litrów na 100 kilometrów. Średnie zużycie paliwa na każde 100 km całej trasy wyniosło
A) 8 litrów. B) 8,5 litra. C) 7 litrów. D) 9 litrów.
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 25% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,75 B) 0,25 C) 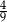 D)
D) 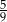
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 40% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,6 B) 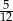 C)
C) 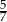 D) 0,4
D) 0,4
Zapisano trzy różne liczby, których średnia arytmetyczna jest równa 4, oraz dwie inne liczby, których średnia arytmetyczna jest równa 2. Uzasadnij, że średnia arytmetyczna zestawu tych pięciu liczb jest równa 3,2. Zapisz obliczenia.
Zapisano dwie różne liczby, których średnia arytmetyczna jest równa 4, oraz trzy inne liczby, których średnia arytmetyczna jest równa 2. Uzasadnij, że średnia arytmetyczna zestawu tych pięciu liczb jest równa 2,8. Zapisz obliczenia.
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest wygrywający, jest równe
A) 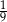 B)
B) 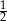 C)
C) 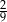 D)
D) 
Na loterii stosunek liczby losów wygrywających do liczby losów przegrywających jest równy 2 : 7. Zakupiono jeden los z tej loterii. Prawdopodobieństwo zdarzenia polegającego na tym, że zakupiony los jest przegrywający, jest równe
A) 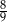 B)
B) 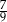 C)
C) 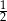 D)
D) 
Kąt między cięciwą 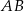 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 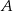 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 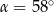 . Wówczas
. Wówczas
A) 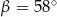 B)
B) 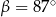 C)
C) 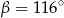 D)
D) 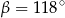
Punkty 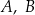 oraz
oraz 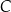 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 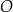 . Prosta
. Prosta 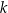 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 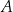 i tworzy z cięciwą
i tworzy z cięciwą 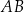 kąt o mierze
kąt o mierze 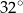 . Ponadto odcinek
. Ponadto odcinek 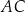 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 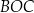 jest równa
jest równa
A) 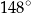 B)
B) 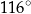 C)
C) 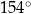 D)
D) 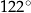
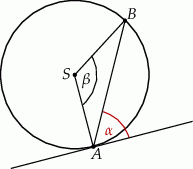
Kąt między cięciwą 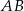 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 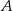 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 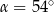 . Wówczas
. Wówczas
A) 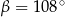 B)
B) 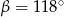 C)
C) 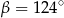 D)
D) 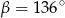
Punkty  oraz
oraz 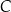 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 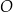 . Prosta
. Prosta 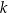 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 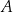 i tworzy z cięciwą
i tworzy z cięciwą 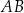 kąt o mierze
kąt o mierze 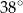 . Ponadto odcinek
. Ponadto odcinek 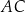 jest średnicą tego okręgu (zobacz rysunek).
jest średnicą tego okręgu (zobacz rysunek).

Miara kąta rozwartego 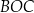 jest równa
jest równa
A) 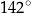 B)
B) 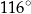 C)
C) 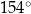 D)
D) 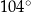
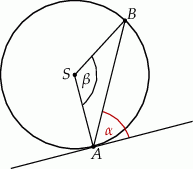
Kąt między cięciwą 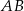 a styczną do okręgu w punkcie
a styczną do okręgu w punkcie 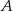 (zobacz rysunek) ma miarę
(zobacz rysunek) ma miarę 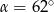 . Wówczas
. Wówczas
A) 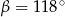 B)
B) 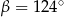 C)
C) 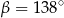 D)
D) 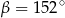
W trzech sadach wiśniowych rosła pewna liczba drzew. W pierwszym sadzie znajdowało się  , a w drugim
, a w drugim 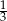 wszystkich drzew. W trzecim rosło 320 drzew. Ile drzew rosło w każdym sadzie?
wszystkich drzew. W trzecim rosło 320 drzew. Ile drzew rosło w każdym sadzie?
Liczba 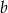 jest 3 razy większa od liczby
jest 3 razy większa od liczby  . Wtedy
. Wtedy
A) 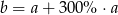 B)
B) 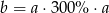 C)
C) 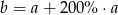 D)
D) 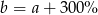
Liczba 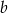 jest 2 razy większa od liczby
jest 2 razy większa od liczby  . Wtedy
. Wtedy
A) 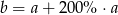 B)
B) 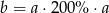 C)
C) 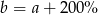 D)
D) 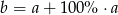
Każdy z dwóch pojemników był początkowo wypełniony 1 kg wodnego roztworu soli o stężeniu 5%. Do pierwszego pojemnika dosypano 150 g soli i dolano 1,55 kg wody. Do drugiego pojemnika dosypano 100 g soli i dolano 0,925 kg wody. Czy stężenie roztworu soli w pojemniku I jest większe niż w pojemniku II? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | stężenia soli w obu pojemnikach są takie same. |
| B) | 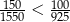 . . |
| C) | 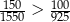 . . |
Prostokątny stół o wymiarach 2 m na 1 m można rozłożyć, tak aby przy dwóch krótszych bokach otrzymać półkola. Oblicz przybliżoną powierzchnię stołu. Przyjmij w obliczeniach 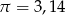 .
.
Na zakup biletów do kina klasa 3a zebrała 360 zł, klasy 3b i 3c po 300 zł, a klasa 3d – 240 zł. Szkole udzielono rabatu i wszystkie bilety kosztowały 1000 zł. Uzyskany rabat podzielono między cztery klasy proporcjonalnie do zebranych kwot. Jaką kwotę zwrócono klasie 3a?
Jacek, Marek, Karol i Andrzej kupili losy na loterii, przy czym Jacek kupił losy za 24 zł, Marek kupił losy za 36 zł, a Karol i Andrzej kupili losy za 30 złoty każdy. Wśród kupionych losów jeden okazał się być wygrywającym i chłopcy otrzymali 600 zł nagrody. Otrzymaną kwotę chłopcy podzielili następująco: każdy otrzymał zwrot kosztów zakupu losów, a pozostałą kwotę podzieli pomiędzy siebie proporcjonalnie do kwot, które przeznaczyli na zakup losów. Ile pieniędzy z nagrody (nie licząc zwrotu kosztów zakupu losów) otrzymał Marek?
Trzy sąsiadki zamówiły wspólnie kawę w sklepie internetowym. Kawa dla pani Malinowskiej miała kosztować 120 zł, a dla pani Wiśniewskiej i dla pani Śliwińskiej – po 90 zł. Sąsiadki przy zakupie otrzymały rabat i za zamówioną kawę zapłaciły 260 zł. Oblicz, ile pieniędzy powinna zapłacić każda z pań, aby jej wpłata była proporcjonalna do pierwotnej wartości zamówienia.
Kwotę 1000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 4% w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa
A) 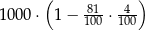 B)
B) 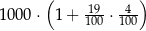
C) 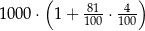 D)
D) 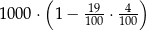
Kwotę 2000 zł ulokowano w banku na roczną lokatę oprocentowaną w wysokości 3% w stosunku rocznym. Po zakończeniu lokaty od naliczonych odsetek odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie roku będzie można wypłacić z banku, jest równa
A) 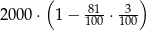 B)
B) 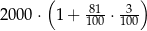
C) 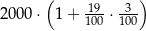 D)
D) 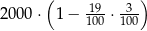
Z jednakowych czworościennych klocków ułożono bryłę mającą kształt czworościanu foremnego.
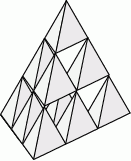
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Utworzona bryła składa się z 10 klocków. | P | F |
| Czworościan foremny o wymiarach takich jak utworzona figura ma objętość 27 razy większą od objętości jednego klocka. | P | F |
Na rysunku przedstawiono prostokąt o bokach długości  i
i 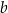 podzielony na sześć kwadratów.
podzielony na sześć kwadratów.
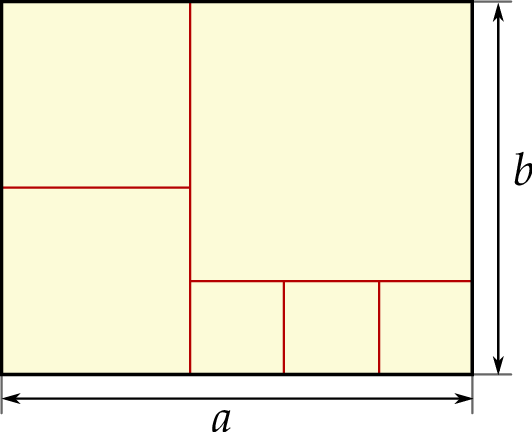
Stosunek długości boków 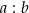 tego prostokąta jest równy
tego prostokąta jest równy
A) 6 : 5 B) 5 : 4 C) 4 : 3 D) 3 : 2
Dany jest wzór na pole powierzchni całkowitej graniastosłupa:
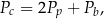
gdzie: 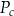 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 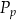 – pole podstawy,
– pole podstawy, 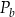 – pole powierzchni bocznej. Pole podstawy
– pole powierzchni bocznej. Pole podstawy 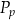 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 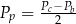 B)
B) 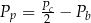 C)
C) 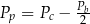 D)
D) 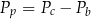
Dany jest wzór na pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego:
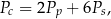
gdzie: 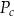 – pole powierzchni całkowitej,
– pole powierzchni całkowitej, 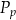 – pole podstawy,
– pole podstawy, 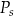 – pole powierzchni jednej ściany bocznej. Pole ściany bocznej
– pole powierzchni jednej ściany bocznej. Pole ściany bocznej 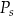 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 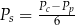 B)
B) 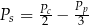 C)
C) 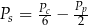 D)
D) 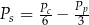
Jacek z 14 jednakowych sześciennych kostek skleił figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.
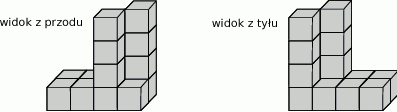
Całą figurę, również od spodu, Jacek pomalował. Ile sześciennych kostek ma pomalowane dokładnie 4 ściany?
A) 8 B) 7 C) 6 D) 5
Dagmara z 20 jednakowych sześciennych kostek skleiła figurę, której widok z przodu i z tyłu przedstawiono na rysunkach.

Całą figurę, również od spodu, Dagmara pomalowała. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dokładnie 7 kostek ma pomalowane dokładnie 3 ściany. | P | F |
| Dokładnie 7 kostek ma pomalowane dokładnie 2 ściany. | P | F |
Trójkąt, w którym długości boków są do siebie w stosunku 3 : 4 : 5 nazywa się trójkątem egipskim. Z odcinków o jakich długościach nie można zbudować trójkąta egipskiego?
A) 6, 8, 10 B) 9, 12, 15 C) 12, 20, 25 D) 21, 28, 35
Oblicz pole prostokąta o wierzchołkach: 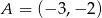 ,
, 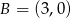 ,
, 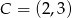 ,
, 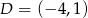 .
.
Oblicz pole prostokąta o wierzchołkach: 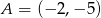 ,
, 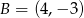 ,
, 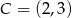 ,
, 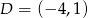 .
.
Oblicz pole prostokąta o wierzchołkach: 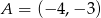 ,
, 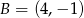 ,
, 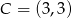 ,
, 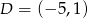 .
.
Oblicz pole prostokąta o wierzchołkach: 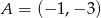 ,
, 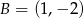 ,
, 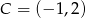 ,
, 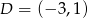 .
.
Oblicz 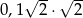 .
.
Oblicz 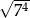 .
.
Oblicz 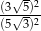 .
.
Oblicz 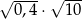 .
.
Oblicz 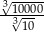 .
.
Oblicz 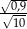 .
.
Oblicz 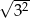 .
.
Oblicz 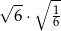 .
.
Oblicz 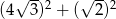 .
.
Oblicz 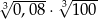 .
.
Oblicz 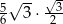 .
.
Oblicz 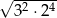 .
.
Oblicz 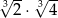 .
.
Oblicz 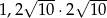 .
.
Oblicz 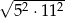 .
.
Do pudełka włożono 48 kul w różnych kolorach. Prawdopodobieństwo wylosowania kuli czerwonej jest równe  , a prawdopodobieństwo wylosowania kuli żółtej jest równe
, a prawdopodobieństwo wylosowania kuli żółtej jest równe 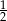 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pudełku jest trzy więcej kul czerwonych niż żółtych. | P | F |
| W pudełku może być 16 kul zielonych. | P | F |
