Ze zbioru kolejnych liczb naturalnych 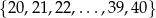 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
A) 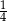 B)
B) 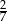 C)
C) 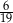 D)
D) 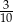
/Szkoła podstawowa
Ze zbioru kolejnych liczb naturalnych 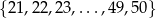 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
A) 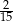 B)
B)  C)
C) 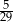 D)
D) 
Wykres przedstawia zależność objętości wody w zbiorniku deszczowym od czasu padania deszczu.
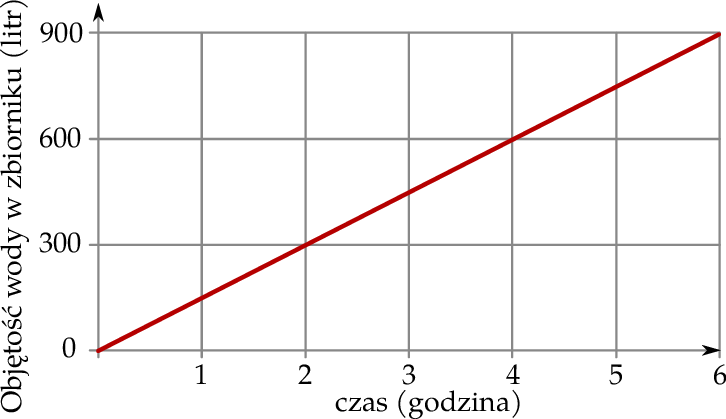
Ile litrów wody przybywa w zbiorniku w czasie 40 minut padania deszczu?
A) 90 litrów B) 100 litrów C) 112,5 litra D) 120 litrów
Na rysunkach I, II i III dane są trzy trójkąty.
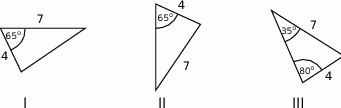
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
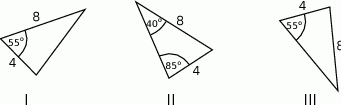
Na których rysunkach trójkąty są przystające?
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
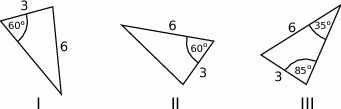
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Długości boków trójkąta równoramiennego przedstawionego na rysunku opisano wyrażeniami algebraicznymi.
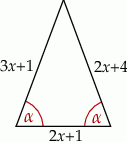
Obwód tego trójkąta jest równy
A) 13 B) 21 C) 27 D) 30
Długości boków trójkąta równoramiennego przedstawionego na rysunku opisano wyrażeniami algebraicznymi.
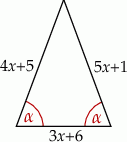
Obwód tego trójkąta jest równy
A) 42 B) 60 C) 48 D) 39
Jaką wysokość ma trójkąt równoboczny o boku 4?
Rysunek przedstawia wykres pewnej funkcji  .
.
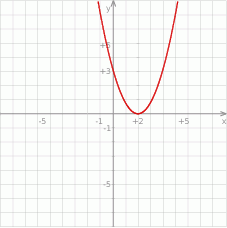
- Odczytaj z wykresu wartości:
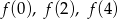 .
. - Dla jakich argumentów funkcja przyjmuje wartość 3?
- Dla jakiego argumentu funkcja przyjmuje wartość najmniejszą?
Parkieciarz w ciągu 6 dni ułożył parkiet liczący 4800 klepek.
| Dzień | Liczba ułożonych klepek | Czas pracy |
| 1. | 700 | 5 h 40 min |
| 2. | 900 | 6 h |
| 3. | 600 | 5 h 20 min |
| 4. | 1000 | 6 h 30 min |
| 5. | 1100 | 6 h 10 min |
| 6. | 500 | 4 h 20 min |
A) Parkieciarz średnio układał 800 klepek dziennie.
B) Trzeciego dnia parkieciarz ułożył 12,5% parkietu.
C) W ciągu dwóch ostatnich dni parkieciarz ułożył
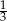 całego parkietu.
całego parkietu. D) Łączny czas pracy parkieciarza w ciągu trzech pierwszych dni był krótszy, niż łączny czas pracy w ciągu trzech następnych dni.
Parkieciarz w ciągu 6 dni ułożył parkiet liczący 4800 klepek.
| Dzień | Liczba ułożonych klepek | Czas pracy |
| 1. | 700 | 5 h 40 min |
| 2. | 900 | 6 h |
| 3. | 600 | 5 h 20 min |
| 4. | 1000 | 6 h 30 min |
| 5. | 1100 | 6 h 10 min |
| 6. | 500 | 4 h 20 min |
| W ciągu dwóch dni pracy tempo układania klepek było mniejsze niż 2 klepki na minutę. | P | F |
| Najwolniej parkieciarz układał klepki 6 dnia. | P | F |
W układzie współrzędnych zaznaczono wierzchołki 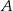 i
i 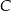 kwadratu
kwadratu 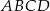 .
.
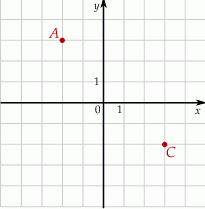
Pole kwadratu 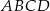 jest równe
jest równe
A) 25 B) 20 C) 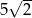 D) 5
D) 5
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
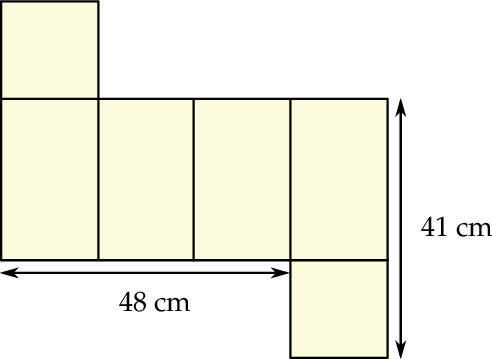
Oblicz objętość tego graniastosłupa.
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
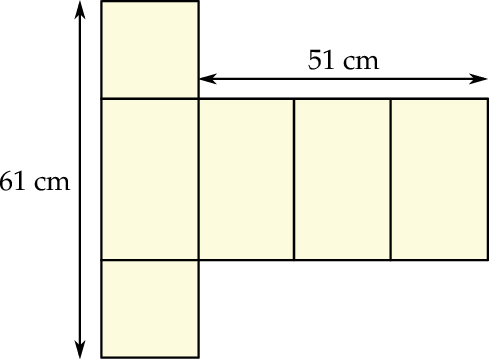
Oblicz objętość tego graniastosłupa.
Prostopadłościan o wymiarach 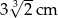 ,
, 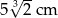 i
i 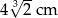 podzielono na 60 jednakowych sześcianów. Objętość jednego sześcianu jest równa
podzielono na 60 jednakowych sześcianów. Objętość jednego sześcianu jest równa
A) 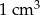 B)
B) 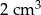 C)
C) 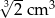 D)
D) 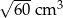
Czy stół, którego blat ma kształt koła o polu 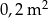 można zakryć prostokątnym obrusem o szerokości 50 cm i długości 75 cm?
można zakryć prostokątnym obrusem o szerokości 50 cm i długości 75 cm?
Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | średnica stołu jest mniejsza od przekątnej prostokąta. |
| B) | średnica stołu jest mniejsza od każdego z boków prostokąta. |
| C) | średnica stołu jest większa od przekątnej prostokąta. |
| D) | średnica stołu jest większa od jednego z boków prostokąta. |
Jeden bok prostokąta zwiększono o 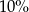 . O ile procent zmieniło się pole prostokąta?
. O ile procent zmieniło się pole prostokąta?
Wykaż, że dla dowolnej liczby całkowitej 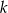 różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od
różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od 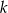 jest równa -2.
jest równa -2.
W zagajniku rosną trzy gatunki drzew: buki, brzozy i świerki. Buków jest o 40% więcej niż brzóz i o 15 więcej niż świerków. Świerków jest o 30% więcej niż brzóz. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W tym zagajniku rośnie ponad 200 buków. | P | F |
| Liczba świerków w tym zagajniku jest o 10% mniejsza od liczby buków. | P | F |
Liczbą podzielną przez 12 i 18 jest
A) 4734 B) 7212 C) 2484 D) 4944
Firma przesyłkowa Pudełko korzysta z paczkomatów do samodzielnego nadawania i odbierania przesyłek przez klientów. Firma oferuje trzy rodzaje przesyłek:
| Gabaryt | Maksymalne wymiary | Cena nadania paczki |
| A | 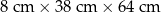 | 6,40 zł |
| B | 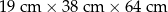 | 11,20 zł |
| C | 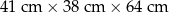 | 15,40 zł |
| Nr zlecenia | Wymiary 1 paczki | Liczba paczek |
| 1 | 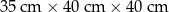 | 3 |
| 2 | 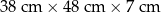 | 7 |
| 3 | 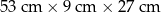 | 5 |
| 4 | 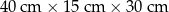 | 4 |
Ile z tych zleceń może zostać zrealizowanych w cenie niższej niż 50 zł?
A) Jedno. B) Dwa. C) Trzy. D) Cztery.
Firma przesyłkowa Pudełko korzysta z paczkomatów do samodzielnego nadawania i odbierania przesyłek przez klientów. Firma oferuje trzy rodzaje przesyłek:
| Gabaryt | Maksymalne wymiary | Cena nadania paczki |
| A | 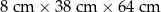 | 6,40 zł |
| B | 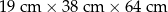 | 11,20 zł |
| C | 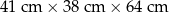 | 15,40 zł |
| Maksymalna objętość paczki gabarytu B jest co najmniej dwa razy większa niż objętość paczki gabarytu A. | P | F |
| Pięć paczek gabarytu A może mieć większą całkowitą objętość niż maksymalna paczka gabarytu C. | P | F |
W trzech salach lekcyjnych było początkowo 44 uczniów. Gdy z trzeciej sali 2 uczniów przeszło do pierwszej sali, a z pierwszej sali 6 uczniów przeszło do drugiej sali to okazało się, że w drugiej sali jest dwa razy więcej uczniów niż w pierwszej sali oraz trzy razy więcej uczniów niż w trzeciej sali. Ilu uczniów było początkowo w trzeciej sali?
W prostokącie o obwodzie 24 cm jeden bok jest dłuższy od drugiego o 4 cm. Pole tego prostokąta jest równe
A) 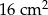 B)
B) 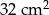 C)
C) 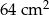 D)
D) 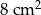
Wartość wyrażenia 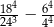 jest równa
jest równa
A) 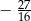 B)
B) 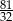 C)
C) 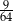 D)
D) 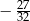
Ala codziennie uczyła się języka hiszpańskiego. Na diagramie przedstawiono, ile czasu przeznaczyła na naukę tego języka w kolejnych dniach tygodnia od poniedziałku do soboty.
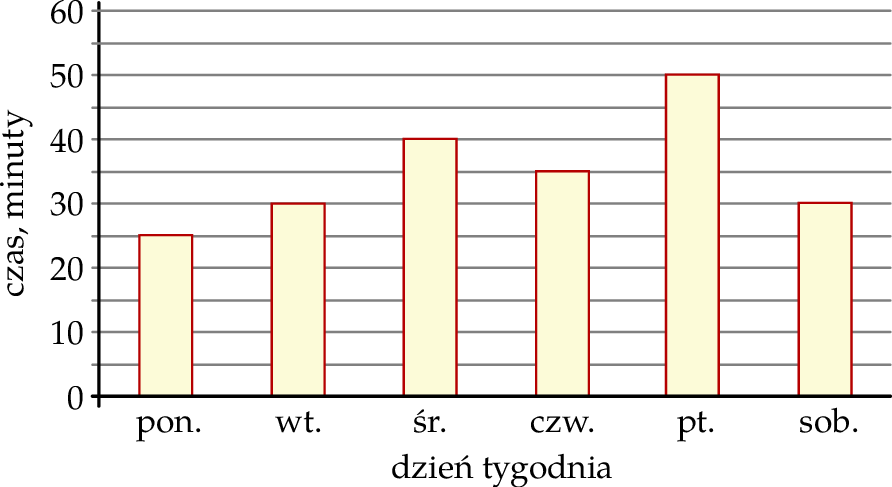
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Ala przez cztery dni – od poniedziałku do czwartku – na naukę języka hiszpańskiego przeznaczyła łącznie 2 godziny i 10 minut. | P | F |
| Na naukę języka hiszpańskiego w sobotę Ala przeznaczyła o 40% czasu mniej niż w piątek. | P | F |

