W wypożyczalni Gierka za wypożyczenie gry planszowej trzeba zapłacić 8 zł za 3 dni i dodatkowo po 2,50 zł za każdy kolejny dzień wypożyczenia. Natomiast w wypożyczalni Planszówka płaci się 12 zł za 3 dni i po 2 zł za każdy kolejny dzień. Przy jakiej liczbie dni koszty wypożyczenia tej gry w jednej i drugiej wypożyczalni są jednakowe?
/Szkoła podstawowa
W basenie ogrodowym było 100 litrów wody, gdy odkręcono zawór doprowadzający wodę do basenu. Woda wypływa z zaworu z szybkością 15 litrów na minutę.
- Zapisz wzór i narysuj wykres funkcji opisującej zależność ilości wody w basenie od czasu.
- Ile wody będzie w basenie po 5 minutach?
- Po ilu minutach w basenie będzie 400 litrów wody?
Kasia przygotowując się do egzaminu rozwiązywała zadania w ciągu 3 dni. Pierwszego dnia rozwiązała 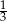 zadań i jeszcze 4 zadania. Drugiego dnia połowę pozostałych i jeszcze 3 zadania. Trzeciego dnia pozostałych 17 zadań. Ile zadań rozwiązała w ciągu 3 dni?
zadań i jeszcze 4 zadania. Drugiego dnia połowę pozostałych i jeszcze 3 zadania. Trzeciego dnia pozostałych 17 zadań. Ile zadań rozwiązała w ciągu 3 dni?
Uczniów na przedstawienie przewieziono trzema samochodami. W każdym samochodzie jest 49 miejsc.

Oceń, czy podane zdania są prawdziwe. Zaznacz P (prawda) lub F (fałsz).
| Samochodami przewieziono razem 102 uczniów. | P | F |
Samochodem 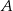 przewieziono więcej uczniów niż samochodem przewieziono więcej uczniów niż samochodem 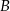 . . | P | F |
W samochodzie 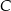 zostało jeszcze 12 wolnych miejsc. zostało jeszcze 12 wolnych miejsc. | P | F |
W samochodzie  było najwięcej wolnych miejsc. było najwięcej wolnych miejsc. | P | F |
Spośród poniższych danych wybierz potrzebne informacje do udzielenia odpowiedzi na pytanie: Ile kilogramów mleka potrzeba na zrobienie jednej kostki masła? Wynik zaokrąglij do 0,1 kg.
1. Masło to tłuszcz jadalny w postaci stałej który otrzymuje sie z mleka.
2. 3,5% masy mleka to masa tłuszczu.
3. Jedna kostka masła ma masę 0,25 kg.
4. Masło składa się z ok. 82% tłuszczu i 16% wody.
5. Naturalnym kolorem masła jest kolor kremowy.
Cenę pewnego towaru podwyższono najpierw o 30%, a potem obniżono o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 21% C) 22% D) 17%
Cenę pewnego towaru podniesiono o 10%, a następnie obniżono o 15%. Cena po obu zmianach stanowi 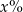 początkowej ceny towaru. Zatem
początkowej ceny towaru. Zatem
A) 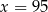 B)
B) 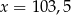 C)
C) 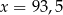 D)
D) 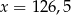
Cenę roweru obniżono o 20%, a po miesiącu podniesiono o 10%. W wyniku obu operacji finansowych cena roweru zmniejszyła się o
A) 10% B) 11% C) 12% D) 15%
Dane są cztery liczby:
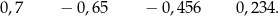
Suma największej i najmniejszej spośród tych liczb jest równa A/B.
A) 1,35 B) 0,05
Na osi liczbowej odległość między punktami odpowiadającymi liczbom 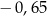 oraz
oraz 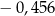 jest równa C/D.
jest równa C/D.
C) 0,194 D) 1,106
Wiadomo, że 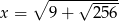 . Wynika stąd, że
. Wynika stąd, że
A) 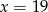 B)
B) 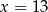 C)
C) 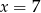 D)
D) 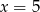
Wiadomo, że 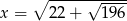 . Wynika stąd, że
. Wynika stąd, że
A) 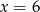 B)
B) 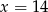 C)
C) 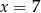 D)
D) 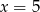
Liczba  jest równa
jest równa
A) 5 B) 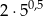 C)
C) 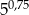 D)
D) 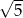
Wiadomo, że 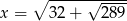 . Wynika stąd, że
. Wynika stąd, że
A) 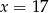 B)
B) 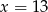 C)
C) 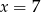 D)
D) 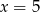
Grupa turystów w ciągu pierwszej godziny marszu pokonała pewien odcinek trasy. W każdej następnej godzinie pokonywany dystans był o 0,5 km krótszy od dystansu pokonanego w poprzedniej godzinie. W ciągu pierwszych pięciu godzin marszu turyści przeszli łącznie 17,5 km trasy. Odcinek trasy, który turyści przeszli w pierwszej godzinie marszu, miał długość
A) 3,1 km B) 3,5 km C) 3,9 km D) 4,0 km E) 4,5 km
Grupa turystów w ciągu pierwszej godziny marszu pokonała pewien odcinek trasy. W każdej następnej godzinie pokonywany dystans był o 0,5 km dłuższy od dystansu pokonanego w poprzedniej godzinie. W ciągu pierwszych sześciu godzin marszu turyści przeszli łącznie 16,5 km trasy. Odcinek trasy, który turyści przeszli w pierwszej godzinie marszu, miał długość
A) 4 km B) 2,5 km C) 3,5 km D) 1,5 km E) 2,1 km
Ze zbioru kolejnych liczb naturalnych 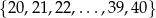 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
A) 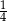 B)
B) 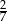 C)
C) 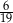 D)
D) 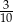
Ze zbioru kolejnych liczb naturalnych 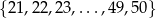 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 6 jest równe
A) 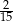 B)
B)  C)
C) 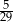 D)
D) 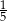
Wykres przedstawia zależność objętości wody w zbiorniku deszczowym od czasu padania deszczu.
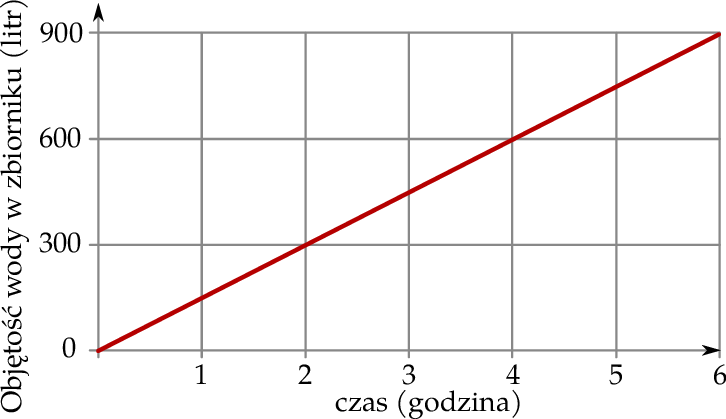
Ile litrów wody przybywa w zbiorniku w czasie 40 minut padania deszczu?
A) 90 litrów B) 100 litrów C) 112,5 litra D) 120 litrów
Na rysunkach I, II i III dane są trzy trójkąty.
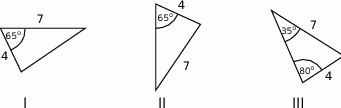
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
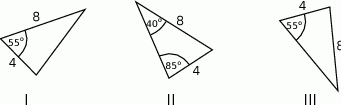
Na których rysunkach trójkąty są przystające?
A) I i II B) I i III C) II i III D) I, II i III
Na rysunkach I, II i III dane są trzy trójkąty.
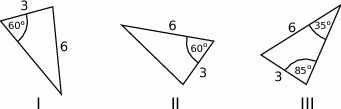
Przystające są trójkąty tylko na rysunkach
A) I i II B) I i III C) II i III D) I, II i III
Długości boków trójkąta równoramiennego przedstawionego na rysunku opisano wyrażeniami algebraicznymi.
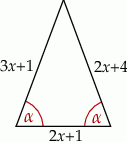
Obwód tego trójkąta jest równy
A) 13 B) 21 C) 27 D) 30
Długości boków trójkąta równoramiennego przedstawionego na rysunku opisano wyrażeniami algebraicznymi.
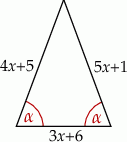
Obwód tego trójkąta jest równy
A) 42 B) 60 C) 48 D) 39
Jaką wysokość ma trójkąt równoboczny o boku 4?
Rysunek przedstawia wykres pewnej funkcji 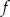 .
.
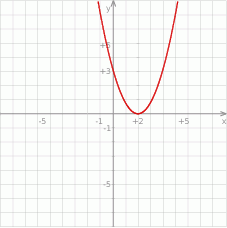
- Odczytaj z wykresu wartości:
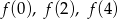 .
. - Dla jakich argumentów funkcja przyjmuje wartość 3?
- Dla jakiego argumentu funkcja przyjmuje wartość najmniejszą?
Parkieciarz w ciągu 6 dni ułożył parkiet liczący 4800 klepek.
| Dzień | Liczba ułożonych klepek | Czas pracy |
| 1. | 700 | 5 h 40 min |
| 2. | 900 | 6 h |
| 3. | 600 | 5 h 20 min |
| 4. | 1000 | 6 h 30 min |
| 5. | 1100 | 6 h 10 min |
| 6. | 500 | 4 h 20 min |
A) Parkieciarz średnio układał 800 klepek dziennie.
B) Trzeciego dnia parkieciarz ułożył 12,5% parkietu.
C) W ciągu dwóch ostatnich dni parkieciarz ułożył
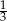 całego parkietu.
całego parkietu. D) Łączny czas pracy parkieciarza w ciągu trzech pierwszych dni był krótszy, niż łączny czas pracy w ciągu trzech następnych dni.
Parkieciarz w ciągu 6 dni ułożył parkiet liczący 4800 klepek.
| Dzień | Liczba ułożonych klepek | Czas pracy |
| 1. | 700 | 5 h 40 min |
| 2. | 900 | 6 h |
| 3. | 600 | 5 h 20 min |
| 4. | 1000 | 6 h 30 min |
| 5. | 1100 | 6 h 10 min |
| 6. | 500 | 4 h 20 min |
| W ciągu dwóch dni pracy tempo układania klepek było mniejsze niż 2 klepki na minutę. | P | F |
| Najwolniej parkieciarz układał klepki 6 dnia. | P | F |
W układzie współrzędnych zaznaczono wierzchołki 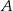 i
i 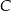 kwadratu
kwadratu 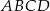 .
.
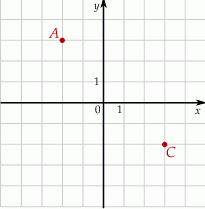
Pole kwadratu 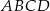 jest równe
jest równe
A) 25 B) 20 C) 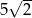 D) 5
D) 5
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
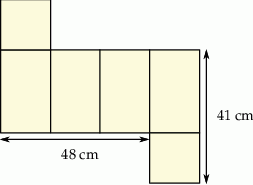
Oblicz objętość tego graniastosłupa.
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
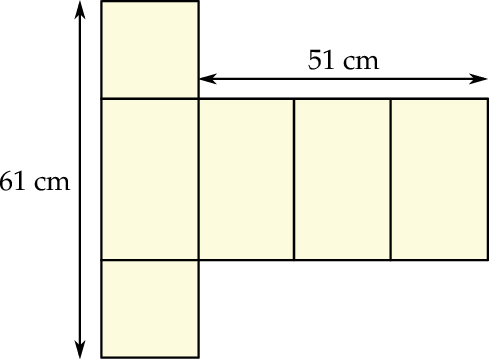
Oblicz objętość tego graniastosłupa.
Prostopadłościan o wymiarach 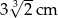 ,
, 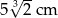 i
i 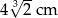 podzielono na 60 jednakowych sześcianów. Objętość jednego sześcianu jest równa
podzielono na 60 jednakowych sześcianów. Objętość jednego sześcianu jest równa
A) 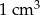 B)
B) 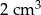 C)
C) 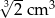 D)
D) 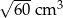
Czy stół, którego blat ma kształt koła o polu 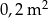 można zakryć prostokątnym obrusem o szerokości 50 cm i długości 75 cm?
można zakryć prostokątnym obrusem o szerokości 50 cm i długości 75 cm?
Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | średnica stołu jest mniejsza od przekątnej prostokąta. |
| B) | średnica stołu jest mniejsza od każdego z boków prostokąta. |
| C) | średnica stołu jest większa od przekątnej prostokąta. |
| D) | średnica stołu jest większa od jednego z boków prostokąta. |

