Adam przygotował karty do gry z czterech arkuszy kartonu. Najpierw podzielił każdy arkusz kartonu na cztery części, a następnie każdą z nich ponownie podzielił na cztery części. Tak powstał komplet kart. W grze bierze udział 5 graczy, z których każdy otrzymuje jednakową liczbę kart. Adam przygotował A/B karty do gry.
A) 32 B) 64
Każdy gracz może otrzymać maksymalnie C/D kart.
C) 12 D) 13
/Szkoła podstawowa
Oskar przygotował karty do gry z trzech arkuszy kartonu. Najpierw podzielił każdy arkusz kartonu na sześć części, a następnie każdą z nich ponownie podzielił na sześć części. Tak powstał komplet kart. W grze bierze udział 5 graczy, z których każdy otrzymuje jednakową liczbę kart. Oskar przygotował A/B kart(y) do gry.
A) 108 B) 144
Każdy gracz może otrzymać maksymalnie C/D kart(y).
C) 22 D) 21
Z czarnych krążków układane są figury w kształcie kwadratu, według reguły przedstawionej na rysunku.
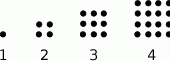
O ile więcej krążków będzie w figurze numer 12 niż w figurze numer 10?
A) 144 B) 44 C) 42 D) 40
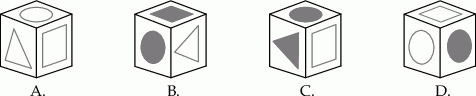
Na kartonowej siatce sześcianu Mariusz nakleił 6 figur tak, jak pokazano na rysunku. Następnie z tej siatki skleił kostkę.
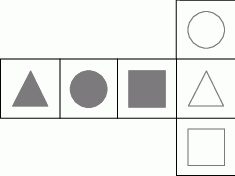
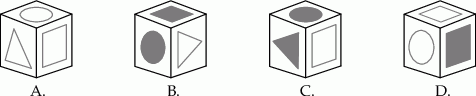
Który rysunek przedstawia kostkę sklejoną przez Mariusza?
Na kartonowej siatce sześcianu Mariusz nakleił 6 figur tak, jak pokazano na rysunku. Następnie z tej siatki skleił kostkę.
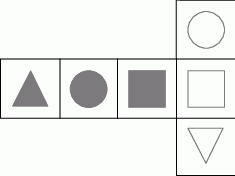
Który rysunek przedstawia kostkę sklejoną przez Mariusza?
Dwa lata temu córka była 6 razy młodsza od matki, a za cztery lata matka będzie 3 razy starsza od córki. Ile lat ma teraz córka?
W równoległoboku  kąt przy wierzchołku
kąt przy wierzchołku  ma większą miarę, niż kąt przy wierzchołku
ma większą miarę, niż kąt przy wierzchołku  . Suma miar pewnych trzech kątów tego równoległoboku jest równa
. Suma miar pewnych trzech kątów tego równoległoboku jest równa 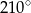 .
.
Miara kąta przy wierzchołku 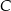 równoległoboku jest równa A/B.
równoległoboku jest równa A/B.
A) 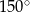 B)
B) 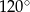
Miara kąta przy wierzchołku 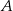 jest C/D razy większa od miary kąta przy wierzchołku
jest C/D razy większa od miary kąta przy wierzchołku 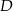 .
.
C) 4 D) 5
Pole prostokąta wynosi 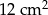 . Pole prostokąta do niego podobnego jest równe
. Pole prostokąta do niego podobnego jest równe 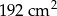 . Skala podobieństwa prostokąta mniejszego do większego jest równa
. Skala podobieństwa prostokąta mniejszego do większego jest równa
A) 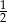 B)
B)  C)
C) 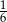 D)
D) 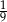
Julia połowę swoich oszczędności przeznaczyła na prezent dla Maćka. 10% tego, co jej zostało, przeznaczyła na prezent dla Dominiki. Ile procent oszczędności pozostało Julii?
A) 25 B) 40 C) 45 D) 55
Wojtek 40% swoich oszczędności przeznaczył na zakup nowego plecaka. Połowę z tego, co mu zostało, przeznaczył na zakup butów. Ile procent oszczędności pozostało Wojtkowi?
A) 10% B) 30% C) 40% D) 20%
Średnia długość życia niedźwiedzia jest 4 razy większa od średniej długości życia lisa. Niektóre osobniki żyją jednak o wiele dłużej. Jeśli niedźwiedź i lis będą żyły o 20 lat dłużej niż średnia długość życia ich gatunków, to niedźwiedź dożyje wieku dwa razy większego od lisa. Ile wynoszą średnie długości życia tych zwierząt?
Suma trzech liczb jest równa 2520. Jakie to liczby jeżeli ich stosunek jest równy 4:5:9?
Czworokąt 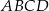 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 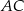 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 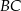 i
i 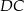 , a kąt
, a kąt 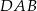 ma miarę
ma miarę 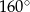 .
.
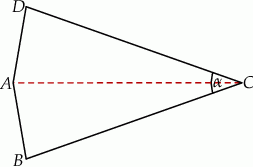
Miara kąta 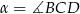 jest równa
jest równa
A) 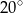 B)
B) 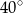 C)
C) 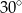 D)
D) 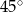
Po dodaniu do zestawu liczb: 10, 4, 5, 9, 12 jednej liczby średnia liczb zmniejszyła się o 1.
Którą z poniższych liczb dopisano?
A) 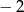 B)
B)  C) 2 D) 3
C) 2 D) 3
Dany jest zestaw liczb: 4, 9, 11, 15, 21. Do podanych liczb dopisano jeszcze jedną liczbę i wtedy średnia arytmetyczna nowego zestawu liczb zwiększyła się o 1. Która liczba została dopisana?
A) 10 B) 12 C) 13 D) 18
Po usunięciu z zestawu liczb: 15, 10, 4, 5, 9, 12, 8 jednej liczby średnia liczb nie zmieniła się.
Którą z poniższych liczb usunięto?
A) 8 B) 9 C) 10 D) 12
Zbiornik z cementem jest opróżniany na znajdujący się pod nim taśmociąg. Na wykresie przedstawiono ilość cementu pozostałego w zbiorniku w zależności od czasu upływającego od momentu rozpoczęcia opróżniania zbiornika.
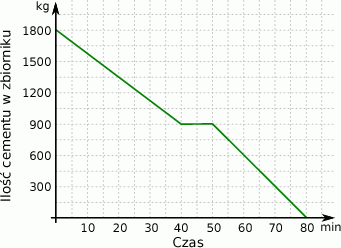
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na 10 minut przed zakończeniem opróżniania zbiornika wciąż było w nim 300 kg cementu. | P | F |
| W trakcie pierwszych dwudziestu minut opróżniania zbiornika wysypano z niego 1350 kg cementu. | P | F |
Zbiornik z cementem jest opróżniany na znajdujący się pod nim taśmociąg. Na wykresie przedstawiono ilość cementu pozostałego w zbiorniku w zależności od czasu upływającego od momentu rozpoczęcia opróżniania zbiornika.
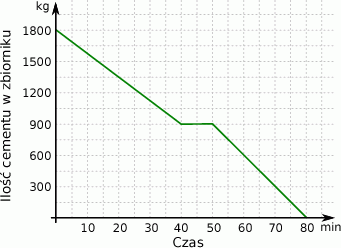
Średnia prędkość z jaką opróżniono pierwszą połowę zawartości zbiornika wyniosła
A) 1350 kg/h B) 800 kg/h C) 2250 kg/h D) 1080 kg/h
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział największego inwestora?
A) 12% B) 32% C) 48% D) 52%
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział najmniejszego inwestora?
A) 2% B) 4% C) 6% D) 8%
Pan Józef odbył podróż pomiędzy czterema miastami: najpierw samolotem pomiędzy miastami 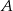 i
i 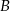 , później samochodem pomiędzy miastami
, później samochodem pomiędzy miastami  i
i 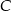 , potem pociągiem między miastami
, potem pociągiem między miastami 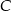 i
i 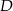 , a na koniec wrócił autokarem do miasta
, a na koniec wrócił autokarem do miasta 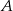 . Na rysunku przedstawiono schemat tej podróży.
. Na rysunku przedstawiono schemat tej podróży.
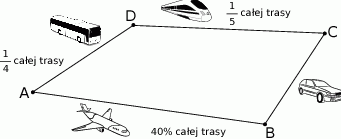
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Droga przebyta samochodem stanowiła mniej niż 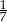 całej trasy podróży. całej trasy podróży. | P | F |
| Dystans pokonany samolotem był dwa razy większy od dystansu pokonanego pociągiem. | P | F |
Pan Józef odbył podróż pomiędzy czterema miastami: najpierw samolotem pomiędzy miastami 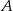 i
i 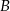 , później samochodem pomiędzy miastami
, później samochodem pomiędzy miastami 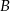 i
i 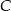 , potem pociągiem między miastami
, potem pociągiem między miastami 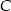 i
i 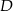 , a na koniec wrócił autokarem do miasta
, a na koniec wrócił autokarem do miasta 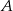 . Na rysunku przedstawiono schemat tej podróży.
. Na rysunku przedstawiono schemat tej podróży.
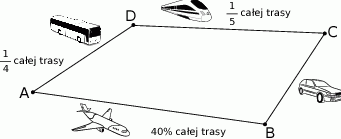
Jeżeli dystans pokonany samolotem był o 300 km większy niż dystans pokonany autokarem, to dystans pokonany samochodem był równy
A) 300 km B) 400 km C) 500 km D) 800 km
W trójkącie 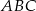 dane są:
dane są: 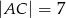 ,
, 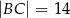 i
i 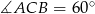 . Oblicz pole trójkąta
. Oblicz pole trójkąta 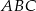 .
.
Rzucamy raz symetryczną sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że w rzucie tą kostką wypadnie liczba oczek większa od 2, ale mniejsza od 6?
A) 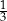 B)
B) 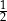 C)
C)  D)
D) 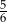
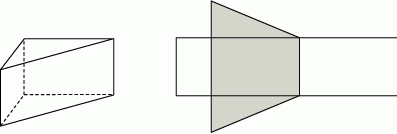
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Dwie dłuższe krawędzie podstawy graniastosłupa mają 12 cm i 13 cm długości, a pole zacieniowanej części siatki graniastosłupa jest równe 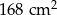 . Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
. Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
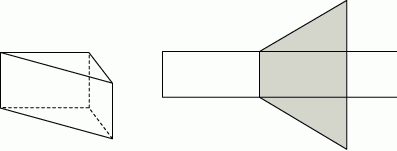
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Najkrótsza krawędź podstawy graniastosłupa ma długość 9 cm, a wysokość graniastosłupa ma długość 8 cm. Pole zacieniowanej części siatki graniastosłupa jest równe 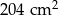 . Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
. Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
Drzewo rzuca cień o długości 11 m, a o tej samej porze cień chłopca o wzroście 170 cm ma długość 2,2 m. Oblicz wysokość drzewa.
Wieża rzuca cień o długości 31,5m. W tym samym czasie wbity pionowo w ziemię pręt o wysokości 1,6m rzuca cień o długości 1,2m. Oblicz wysokość wieży.
Punkt 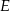 jest środkiem boku
jest środkiem boku 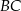 równoległoboku
równoległoboku 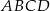 , a odcinek
, a odcinek  przecina przekątną
przecina przekątną 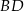 w punkcie
w punkcie 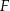 . Wykaż, że
. Wykaż, że 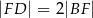 .
.
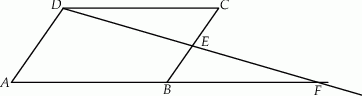
W równoległoboku 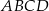 punkt
punkt 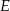 jest środkiem boku
jest środkiem boku 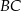 . Z wierzchołka
. Z wierzchołka 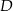 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 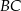 w punkcie
w punkcie 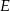 . Proste
. Proste 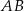 i
i 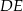 przecinają się w punkcie
przecinają się w punkcie 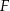 (zobacz rysunek). Wykaż, że punkt
(zobacz rysunek). Wykaż, że punkt 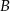 jest środkiem odcinka
jest środkiem odcinka 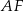 .
.
Pewien towar, obłożony 7–procentowym podatkiem VAT, kosztuje 59,92 zł. Oblicz ile wynosi podatek VAT.

