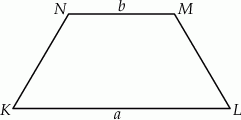
Dany jest trapez równoramienny 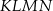 , którego podstawy mają długości
, którego podstawy mają długości 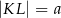 ,
, 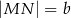 ,
, 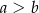 . Kąt
. Kąt 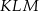 ma miarę
ma miarę 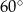 . Długość ramienia
. Długość ramienia 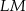 tego trapezu jest równa
tego trapezu jest równa
A) 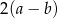 B)
B) 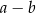 C)
C) 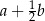 D)
D) 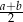
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trapez równoramienny 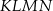 , którego podstawy mają długości
, którego podstawy mają długości 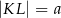 ,
, 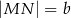 ,
, 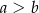 . Kąt
. Kąt 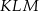 ma miarę
ma miarę 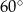 . Długość ramienia
. Długość ramienia 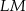 tego trapezu jest równa
tego trapezu jest równa

A) 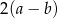 B)
B) 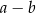 C)
C) 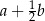 D)
D) 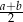
W trapezie równoramiennym  podstawy
podstawy 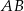 i
i 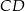 mają długości równe odpowiednio
mają długości równe odpowiednio  i
i 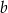 (przy czym
(przy czym 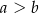 ). Miara kąta ostrego trapezu jest równa
). Miara kąta ostrego trapezu jest równa 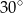 . Wtedy wysokość tego trapezu jest równa
. Wtedy wysokość tego trapezu jest równa
A) 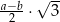 B)
B) 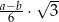 C)
C) 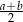 D)
D) 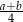
Pensja pana 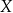 jest o 50% wyższa od średniej krajowej, a pensja pana
jest o 50% wyższa od średniej krajowej, a pensja pana 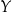 jest o 40% niższa od średniej krajowej. Pensja pana
jest o 40% niższa od średniej krajowej. Pensja pana 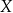 jest wyższa od pensji pana
jest wyższa od pensji pana 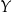
A) o 40% pensji pana 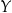 . B) o 90% pensji pana
. B) o 90% pensji pana 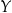 .
.
C) o 150% pensji pana 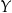 . D) o 275% pensji pana
. D) o 275% pensji pana  .
.
Pensja pana  jest o 50% wyższa od średniej krajowej, a pensja pana
jest o 50% wyższa od średniej krajowej, a pensja pana  jest o 40% niższa od średniej krajowej. Pensja pana
jest o 40% niższa od średniej krajowej. Pensja pana  jest niższa od pensji pana
jest niższa od pensji pana 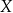
A) o 60% pensji pana 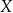 . B) o 73% pensji pana
. B) o 73% pensji pana 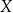 .
.
C) o 90% pensji pana 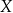 . D) o 150% pensji pana
. D) o 150% pensji pana 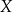 .
.
Objętość metalowej kuli jest równa 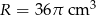 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość tej kuli jest większa niż 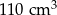 . . | P | F |
Pole powierzchni tej kuli jest równe 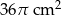 . . | P | F |
Rozważmy treść następującego zadania:
Obwód prostokąta o bokach długości  i
i 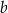 jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 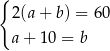 B)
B) 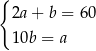 C)
C) 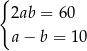 D)
D) 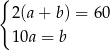
Rozważmy treść następującego zadania:
Pole prostokąta o bokach długości  i
i 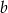 jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 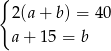 B)
B) 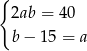 C)
C) 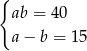 D)
D) 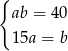
Mediana danych przedstawionych w tabeli liczebności jest równa
| Wartość | 0 | 1 | 2 | 3 |
| Liczebność | 5 | 2 | 1 | 1 |
A) 0 B) 0,5 C) 1 D) 5
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 2 | 4 | 3 | 4 | 5 | 3 |
Mediana tych danych jest równa.
A) 3 B) 3,5 C) 4 D) 5
W pewnej grupie uczniów przeprowadzono ankietę na temat liczby odsłuchanych audiobooków w lutym 2022 roku. Wyniki ankiety przedstawiono w tabeli.
| Liczba odsłuchanych audiobooków | 0 | 1 | 2 | 3 | 4 | 7 |
| Liczba uczniów | 9 | 5 | 3 | 4 | 1 | 3 |
Mediana liczby odsłuchanych audiobooków w tej grupie uczniów jest równa
A) 3 B) 2 C) 1 D) 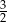
Mediana danych przedstawionych w tabeli liczebności jest równa
| Wartość | 0 | 1 | 2 | 3 |
| Liczebność | 4 | 3 | 2 | 5 |
A) 2 B) 1,5 C) 1 D) 0,5
W tabeli poniżej przedstawione są wyniki pracy klasowej.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba uczniów | 2 | 3 | 7 | 6 | 4 | 2 |
Mediana ocen w tej klasie jest równa
A) 3,5 B) 3 C) 4 D) 4,5
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 4 | 3 | 3 | 4 | 2 | 3 |
Mediana tych danych jest równa.
A) 3 B) 3,5 C) 4 D) 5
Abiturient jednego z liceów zestawił w tabeli oceny ze swojego świadectwa ukończenia szkoły.
| Ocena | 6 | 5 | 4 | 3 | 2 |
| Liczba ocen | 2 | 3 | 5 | 5 | 1 |
Mediana przedstawionego zestawu danych jest równa
A) 3 B) 3,5 C) 4 D) 4,5
W tabeli poniżej przedstawione są wyniki pracy klasowej.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 2 | 5 | 2 | 12 | 5 | 1 |
Mediana ocen w tej klasie jest równa
A) 3 B) 3,5 C) 4 D) 5
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 1 cm krótsza od boku tego trójkąta.
Wyznacz pole trójkąta równobocznego, którego wysokość jest o 2 cm krótsza od boku tego trójkąta.
Łąka ma kształt równoległoboku i jest podzielona na dwie części  i
i  , tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.
, tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.
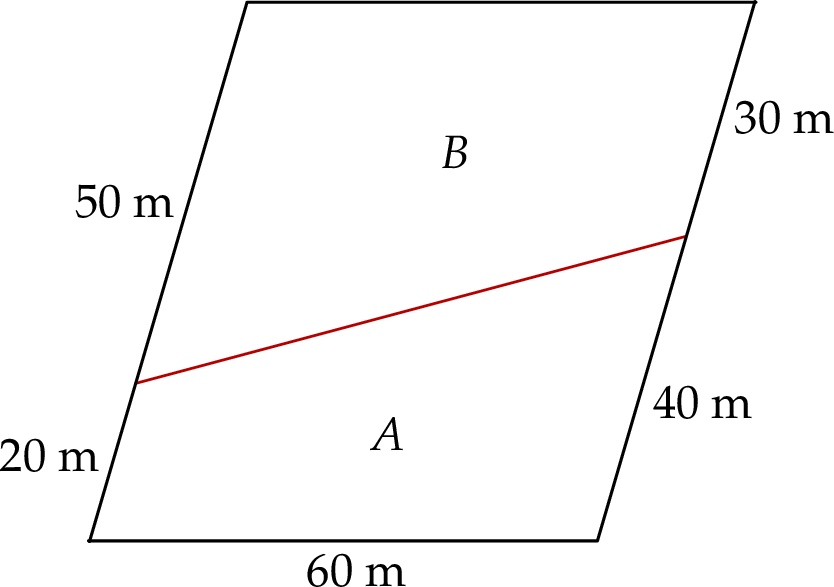
Kosiarka w ciągu każdej godziny swojej pracy kosi trawę z powierzchni o takim samym polu. Kosiarka całą łąkę skosiła w ciągu 14 godzin. Oblicz, ile godzin potrzebowałaby ta kosiarka na skoszenie trawy z części  jest łąki.
jest łąki.
Przyjmijmy, że Ziemia ma kształt kuli, oraz że równik ma długość 40 000 km. Jaki jest promień Ziemi? W obliczeniach przyjmij, że  . Wynik podaj z dokładnością do 1 km.
. Wynik podaj z dokładnością do 1 km.
Długość równoleżnika na szerokości geograficznej 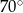 wynosi 13 700 km. Jaki jest promień tego równoleżnika? W obliczeniach przyjmij, że
wynosi 13 700 km. Jaki jest promień tego równoleżnika? W obliczeniach przyjmij, że 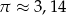 . Wynik podaj z dokładnością do 1 km.
. Wynik podaj z dokładnością do 1 km.
Długość równoleżnika na szerokości geograficznej 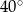 wynosi 30 700 km. Jaki jest promień tego równoleżnika? W obliczeniach przyjmij, że
wynosi 30 700 km. Jaki jest promień tego równoleżnika? W obliczeniach przyjmij, że 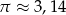 . Wynik podaj z dokładnością do 1 km.
. Wynik podaj z dokładnością do 1 km.
Długość równoleżnika na szerokości geograficznej 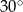 wynosi 34 700 km. Jaki jest promień tego równoleżnika? W obliczeniach przyjmij, że
wynosi 34 700 km. Jaki jest promień tego równoleżnika? W obliczeniach przyjmij, że 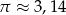 . Wynik podaj z dokładnością do 1 km.
. Wynik podaj z dokładnością do 1 km.
Na ulicznym straganie z kwiatami sprzedano tyle samo róż, co tulipanów oraz 16 goździków. Goździki stanowiły 12,5% liczby sprzedanych kwiatów. Ile tulipanów sprzedano na straganie?
A) 56 B) 28 C) 64 D) 112
Adam przygotował karty do gry z czterech arkuszy kartonu. Najpierw podzielił każdy arkusz kartonu na cztery części, a następnie każdą z nich ponownie podzielił na cztery części. Tak powstał komplet kart. W grze bierze udział 5 graczy, z których każdy otrzymuje jednakową liczbę kart. Adam przygotował A/B karty do gry.
A) 32 B) 64
Każdy gracz może otrzymać maksymalnie C/D kart.
C) 12 D) 13
Oskar przygotował karty do gry z trzech arkuszy kartonu. Najpierw podzielił każdy arkusz kartonu na sześć części, a następnie każdą z nich ponownie podzielił na sześć części. Tak powstał komplet kart. W grze bierze udział 5 graczy, z których każdy otrzymuje jednakową liczbę kart. Oskar przygotował A/B kart(y) do gry.
A) 108 B) 144
Każdy gracz może otrzymać maksymalnie C/D kart(y).
C) 22 D) 21
Z czarnych krążków układane są figury w kształcie kwadratu, według reguły przedstawionej na rysunku.
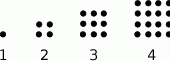
O ile więcej krążków będzie w figurze numer 12 niż w figurze numer 10?
A) 144 B) 44 C) 42 D) 40
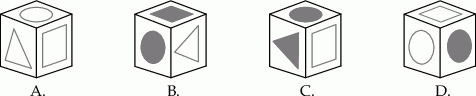
Na kartonowej siatce sześcianu Mariusz nakleił 6 figur tak, jak pokazano na rysunku. Następnie z tej siatki skleił kostkę.
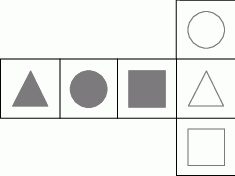
Który rysunek przedstawia kostkę sklejoną przez Mariusza?
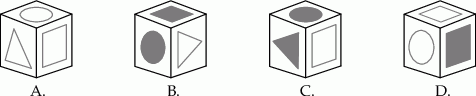
Na kartonowej siatce sześcianu Mariusz nakleił 6 figur tak, jak pokazano na rysunku. Następnie z tej siatki skleił kostkę.
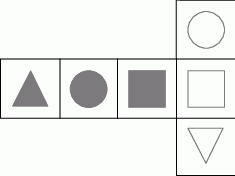
Który rysunek przedstawia kostkę sklejoną przez Mariusza?
Dwa lata temu córka była 6 razy młodsza od matki, a za cztery lata matka będzie 3 razy starsza od córki. Ile lat ma teraz córka?
W równoległoboku  kąt przy wierzchołku
kąt przy wierzchołku 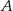 ma większą miarę, niż kąt przy wierzchołku
ma większą miarę, niż kąt przy wierzchołku 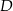 . Suma miar pewnych trzech kątów tego równoległoboku jest równa
. Suma miar pewnych trzech kątów tego równoległoboku jest równa 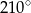 .
.
Miara kąta przy wierzchołku 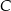 równoległoboku jest równa A/B.
równoległoboku jest równa A/B.
A) 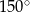 B)
B) 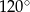
Miara kąta przy wierzchołku 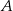 jest C/D razy większa od miary kąta przy wierzchołku
jest C/D razy większa od miary kąta przy wierzchołku 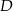 .
.
C) 4 D) 5
Pole prostokąta wynosi 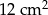 . Pole prostokąta do niego podobnego jest równe
. Pole prostokąta do niego podobnego jest równe 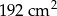 . Skala podobieństwa prostokąta mniejszego do większego jest równa
. Skala podobieństwa prostokąta mniejszego do większego jest równa
A) 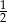 B)
B)  C)
C) 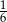 D)
D) 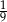
Julia połowę swoich oszczędności przeznaczyła na prezent dla Maćka. 10% tego, co jej zostało, przeznaczyła na prezent dla Dominiki. Ile procent oszczędności pozostało Julii?
A) 25 B) 40 C) 45 D) 55
Wojtek 40% swoich oszczędności przeznaczył na zakup nowego plecaka. Połowę z tego, co mu zostało, przeznaczył na zakup butów. Ile procent oszczędności pozostało Wojtkowi?
A) 10% B) 30% C) 40% D) 20%
Średnia długość życia niedźwiedzia jest 4 razy większa od średniej długości życia lisa. Niektóre osobniki żyją jednak o wiele dłużej. Jeśli niedźwiedź i lis będą żyły o 20 lat dłużej niż średnia długość życia ich gatunków, to niedźwiedź dożyje wieku dwa razy większego od lisa. Ile wynoszą średnie długości życia tych zwierząt?
Suma trzech liczb jest równa 2520. Jakie to liczby jeżeli ich stosunek jest równy 4:5:9?
Czworokąt 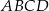 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 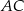 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 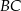 i
i 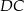 , a kąt
, a kąt 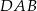 ma miarę
ma miarę 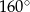 .
.
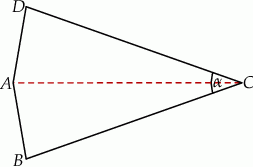
Miara kąta 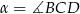 jest równa
jest równa
A) 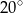 B)
B) 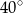 C)
C) 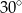 D)
D) 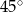
Po dodaniu do zestawu liczb: 10, 4, 5, 9, 12 jednej liczby średnia liczb zmniejszyła się o 1.
Którą z poniższych liczb dopisano?
A) 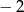 B)
B) 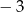 C) 2 D) 3
C) 2 D) 3
Dany jest zestaw liczb: 4, 9, 11, 15, 21. Do podanych liczb dopisano jeszcze jedną liczbę i wtedy średnia arytmetyczna nowego zestawu liczb zwiększyła się o 1. Która liczba została dopisana?
A) 10 B) 12 C) 13 D) 18
Po usunięciu z zestawu liczb: 15, 10, 4, 5, 9, 12, 8 jednej liczby średnia liczb nie zmieniła się.
Którą z poniższych liczb usunięto?
A) 8 B) 9 C) 10 D) 12
