Uczestnicy obozu wędrownego w ciągu drugiego dnia marszu pokonali dwa razy dłuższy odcinek trasy niż w ciągu pierwszego dnia, a w ciągu trzeciego dnia marszu pokonali dystans trzy razy krótszy niż drugiego dnia. W sumie w ciągu trzech dni pokonali trasę długości 60,5 km. Odcinek trasy, który turyści przeszli w drugim dniu wędrówki miał długość
A) 16,5 km B) 33 km C) 36 km D) 11 km
/Szkoła podstawowa
Kasia i Tomek wyruszyli jednocześnie z tego samego domu do szkoły. Długość kroku Kasi jest o 12% mniejsza od kroku Tomka ale Kasia robi o 15% kroków więcej w tym samym czasie niż Tomek. Kto pierwszy dotrze do szkoły.
Bilet do kina kosztuje 15 zł. Ile kosztuje  biletów do kina?
biletów do kina?
Osoba pracująca na umowę-zlecenie otrzymuje wynagrodzenie pomniejszone o 19% podatku. Jak zależy kwota netto 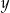 (po potrąceniu podatku) od kwoty brutto
(po potrąceniu podatku) od kwoty brutto  (przed potrąceniem podatku)?
(przed potrąceniem podatku)?
15 litrów wody podzielono równo pomiędzy  osób. Ile litrów wody otrzymała każda z osób?
osób. Ile litrów wody otrzymała każda z osób?
Jaka jest zależność odległości 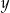 na mapie wykonanej w skali 1:10,000 od rzeczywistej odległości
na mapie wykonanej w skali 1:10,000 od rzeczywistej odległości  w terenie?
w terenie?
Jaka jest cena brutto towaru jeżeli jego cena netto jest równa  , a stawka podatku wynosi 23%?
, a stawka podatku wynosi 23%?
Krowa daje dziennie 12 litrów mleka. Ile mleka daje krowa w ciągu  dni?
dni?
Jeżeli litr benzyny waży 0,7 kg, to ile waży  litrów benzyny?
litrów benzyny?
W beczce o pojemności 200 litrów znajduje się  litrów wody. Wyraź ilość wody
litrów wody. Wyraź ilość wody 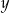 , którą należy wlać do beczki tak, aby była pełna w zależności od
, którą należy wlać do beczki tak, aby była pełna w zależności od  .
.
Ile jest równy obwód kwadratu o boku długości  ?
?
Prostokąt o bokach  i
i 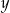 ma pole równe 10. Oblicz
ma pole równe 10. Oblicz 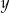 w zależności od
w zależności od  .
.
Chłopiec ma monety po 50 gr i po 20 gr, razem 27 sztuk. Monety mają łączną wartość 8,70 zł. Ile monet po 50 gr, a ile po 20 gr ma chłopiec?
Asia wrzucała do skarbonki monety dwu i pięciozłotowe. Po przeliczeniu zawartości skarbonki okazało się, że w skarbonce znajdowało się 395 monet, a uzbierana kwota wynosi 1195 złotych. Oblicz ile monet każdego rodzaju było w skarbonce.
Rozmieniono 34 złote na 116 monet, wśród których były tylko monety 50 i 20 groszowe. Ile było monet 50 groszowych?
W trójkącie prostokątnym 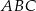 , w którym kąt przy wierzchołku
, w którym kąt przy wierzchołku 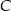 jest kątem prostym, poprowadzono środkowe
jest kątem prostym, poprowadzono środkowe 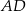 i
i 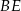 . Udowodnij, że
. Udowodnij, że 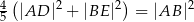 .
.
Powierzchnia Polski wynosi 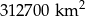 , a liczba ludności około 38 700 000. Oblicz średnią gęstość zaludnienia w naszym kraju.
, a liczba ludności około 38 700 000. Oblicz średnią gęstość zaludnienia w naszym kraju.
Na tablicy zapisano wszystkie różne liczby dwucyfrowe, które jednocześnie spełniają trzy warunki: są mniejsze od 40, są podzielne przez 3, suma cyfr każdej z nich jest większa od 7. Ile liczb zapisano na tablicy?
A) 3 B) 4 C) 5 D) 6
Na tablicy zapisano wszystkie różne liczby dwucyfrowe, które jednocześnie spełniają trzy warunki: są większe od 60, są podzielne przez 3, suma cyfr każdej z nich jest większa od 12. Ile liczb zapisano na tablicy?
A) 3 B) 4 C) 5 D) 6
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 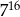 jest 7 razy większa od liczby jest 7 razy większa od liczby 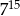 . . | P | F |
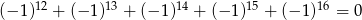 | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 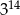 jest 9 razy mniejsza od liczby jest 9 razy mniejsza od liczby 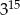 . . | P | F |
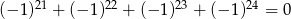 | P | F |
Liczby 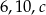 są długościami boków trójkąta prostokątnego. Oblicz
są długościami boków trójkąta prostokątnego. Oblicz  .
.
W trójkącie równoramiennym 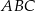 o podstawie
o podstawie 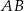 narysowano wysokość
narysowano wysokość 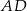 , jak na rysunku. Kąt między tą wysokością a podstawą
, jak na rysunku. Kąt między tą wysokością a podstawą 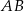 jest równy
jest równy 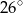 .
.
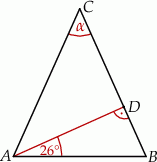
Jaką miarę ma kąt  zaznaczony na rysunku?
zaznaczony na rysunku?
A) 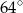 B)
B) 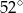 C)
C) 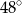 D)
D) 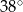
Oblicz 15% wydatków w wysokości 120 zł.
Dane są cztery liczby:
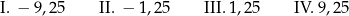
Do której z liczb I–IV należy dodać liczbę 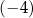 , aby otrzymać liczbę
, aby otrzymać liczbę 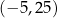 ?
?
A) I B) II C) III D) IV
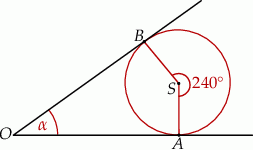
Miara kąta  pod jakim przecinają się styczne do okręgu o środku
pod jakim przecinają się styczne do okręgu o środku 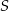 wynosi
wynosi
A) 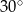 B)
B) 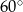 C)
C) 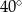 D)
D) 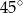
Punkty 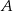 oraz
oraz 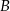 leżą na okręgu o środku
leżą na okręgu o środku 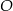 . Proste
. Proste 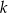 i
i 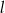 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 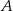 i
i 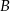 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 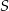 i tworzą kąt o mierze
i tworzą kąt o mierze 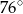 (zobacz rysunek).
(zobacz rysunek).
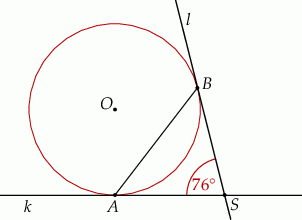
Miara kąta 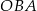 jest równa
jest równa
A) 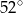 B)
B) 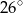 C)
C) 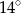 D)
D) 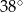
Punkty 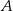 oraz
oraz 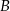 leżą na okręgu o środku
leżą na okręgu o środku 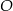 . Proste
. Proste 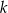 i
i 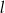 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 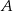 i
i 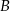 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 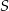 i tworzą kąt o mierze
i tworzą kąt o mierze 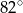 (zobacz rysunek).
(zobacz rysunek).
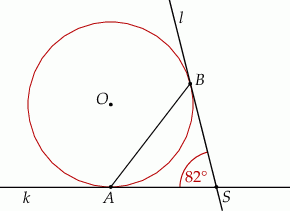
Miara kąta 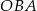 jest równa
jest równa
A) 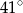 B)
B) 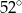 C)
C) 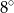 D)
D) 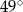
Do okręgu o środku 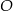 poprowadzono z zewnętrznego punktu
poprowadzono z zewnętrznego punktu 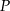 dwie styczne przecinające się w
dwie styczne przecinające się w 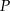 pod kątem
pod kątem 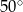 (zobacz rysunek). Punktami styczności są, odpowiednio, punkty
(zobacz rysunek). Punktami styczności są, odpowiednio, punkty 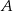 i
i 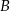 .
.
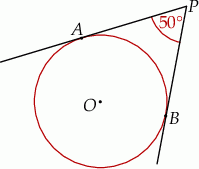
Kąt 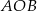 ma miarę
ma miarę
A) 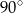 B)
B) 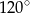 C)
C) 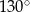 D)
D) 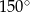
Przez punkty 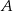 i
i 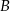 , leżące na okręgu o środku
, leżące na okręgu o środku 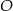 , poprowadzono proste styczne do tego okręgu, przecinające się w punkcie
, poprowadzono proste styczne do tego okręgu, przecinające się w punkcie 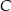 (zobacz rysunek).
(zobacz rysunek).
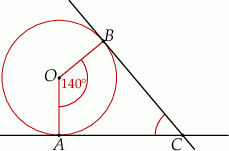
Miara kąta 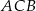 jest równa
jest równa
A) 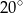 B)
B) 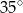 C)
C) 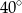 D)
D) 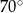
Długość boku 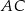 w trójkącie przedstawionym na poniższym rysunku jest równa
w trójkącie przedstawionym na poniższym rysunku jest równa
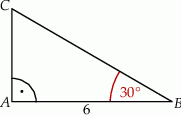
A) 3 B) 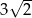 C)
C) 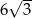 D)
D) 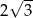
Kwadrat o boku  przedstawiony na rysunku I rozcięto na dwa przystające prostokąty, z których ułożono figurę, jak na rysunku II. Pole ułożonej figury jest równe polu kwadratu.
przedstawiony na rysunku I rozcięto na dwa przystające prostokąty, z których ułożono figurę, jak na rysunku II. Pole ułożonej figury jest równe polu kwadratu.
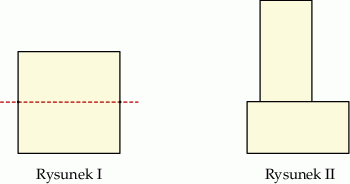
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód ułożonej figury jest większy o 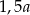 od obwodu kwadratu. od obwodu kwadratu. | P | F |
Obwód ułożonej figury jest równy 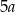 . . | P | F |
Kwadrat o boku  przedstawiony na rysunku I rozcięto na dwa przystające trójkąty, z których ułożono figurę, jak na rysunku II. Pole ułożonej figury jest równe polu kwadratu.
przedstawiony na rysunku I rozcięto na dwa przystające trójkąty, z których ułożono figurę, jak na rysunku II. Pole ułożonej figury jest równe polu kwadratu.
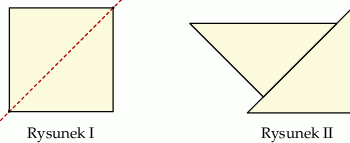
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód ułożonej figury jest większy o mniej niż  od obwodu kwadratu. od obwodu kwadratu. | P | F |
Obwód ułożonej figury jest równy 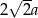 . . | P | F |
Jeżeli do liczby dwucyfrowej dodamy cyfrę jedności, to otrzymamy 38. Jeżeli w tej liczbie przestawimy cyfry i od otrzymanej liczby odejmiemy sumę jej cyfr, to otrzymamy 36. Znajdź tę liczbę.
Suma cyfr pewnej liczby dwucyfrowej wynosi 14. Jeśli do tej liczby dodamy 18, to otrzymamy liczbę utworzoną z tych samych cyfr, ale napisanych w odwrotnej kolejności. Wyznacz tę liczbę.
Suma cyfr pewnej liczby dwucyfrowej wynosi 12. Jeśli do tej liczby dodamy 18, to otrzymamy liczbę utworzoną z tych samych cyfr, ale napisanych w odwrotnej kolejności. Wyznacz tę liczbę.
Samochód kosztował 30000 zł. Jego cenę obniżono o 10%, a następnie cenę po tej obniżce ponownie obniżono o 10%. Po tych obniżkach samochód kosztował
A) 24400 zł B) 24700 zł C) 24000 zł D) 24300 zł
Na początku miesiąca komputer kosztował 3 500 zł. W drugiej dekadzie tego miesiąca cenę komputera obniżono o 10%, a w trzeciej dekadzie cena tego komputera została jeszcze raz obniżona, tym razem o 15%. Innych zmian ceny tego komputera w tym miesiącu już nie było. Cena komputera na koniec miesiąca była równa
A) 3 272,50 zł B) 2 625 zł C) 2 677,50 zł D) 2 800 zł
Pewien towar kosztował 600 zł. Jego cenę obniżono o 15%, a następnie w ramach wyprzedaży sezonowej obniżono o kolejne 10%. Po obu obniżkach towar kosztuje
A) 450 zł B) 459 zł C) 561 zł D) 621 zł
Motor kosztował 4500 zł. Jego cenę obniżono o 10%, a następnie cenę po tej obniżce ponownie obniżono o 10%. Po tych obniżkach motor kosztował
A) 3660 zł B) 3705 zł C) 3645 zł D) 3600 zł
Na początku miesiąca deska snowboardowa kosztowała 4 500 zł. W drugiej dekadzie tego miesiąca cenę deski obniżono o 8%, a w trzeciej dekadzie cena tej deski została jeszcze raz obniżona, tym razem o 12%. Innych zmian ceny tej deski w tym miesiącu już nie było. Cena deski snowboardowej na koniec miesiąca była równa
A) 4 057,20 zł B) 4 086 zł C) 3 643,20 zł D) 3 600 zł
Cena spodni była równa 200 zł. Obniżono tę ceną o 12%, a następnie podwyższono o 12%. Po tych operacjach cena spodni była równa:
A) 200 zł B) 176 zł C) 224,21 zł D) 197,12 zł
Komputer początkowo kosztował 2950 zł. Po trzech miesiącach jego cenę obniżono o 20%. Po kolejnym miesiącu nową cenę obniżono o kolejnych 20%. Cena komputera po tych dwóch obniżkach jest równa
A) 2360 zł B) 1888 zł C) 2832 zł D) 1770 zł
Narty w styczniu kosztowały 640 zł. W lutym obniżono ich cenę o 25%, a w marcu jeszcze o 10%. Cena nart po drugiej obniżce jest równa:
A) 416 zł B) 432 zł C) 605 zł D) 553,50 zł
Dany jest wzór: 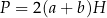 opisujący pole powierzchni bocznej graniastosłupa prostego czworokątnego o wysokości
opisujący pole powierzchni bocznej graniastosłupa prostego czworokątnego o wysokości 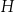 i krawędziach podstawy równych:
i krawędziach podstawy równych: 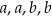 . Którym równaniem opisano
. Którym równaniem opisano 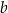 wyznaczone poprawnie z tego wzoru?
wyznaczone poprawnie z tego wzoru?
A) 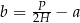 B)
B) 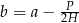 C)
C) 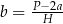 D)
D) 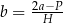
Dany jest wzór na pole powierzchni trapezu:
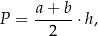
gdzie: 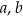 – długości podstaw trapezu,
– długości podstaw trapezu, 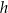 – wysokość trapezu. Długość podstawy
– wysokość trapezu. Długość podstawy  wyznaczona poprawnie z powyższego wzoru opisano równaniem
wyznaczona poprawnie z powyższego wzoru opisano równaniem
A) 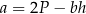 B)
B) 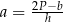 C)
C) 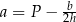 D)
D) 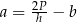
Półkole o promieniu 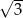 cm zwinięto w stożek.
cm zwinięto w stożek.
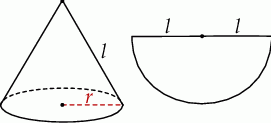
Wysokość tego stożka jest równa
A) 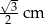 B)
B) 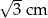 C) 3 cm D) 1,5 cm
C) 3 cm D) 1,5 cm
Na diagramie przedstawiono wyniki (w centymetrach) uzyskane przez zawodników uczestniczących w finale konkursu skoku wzwyż.
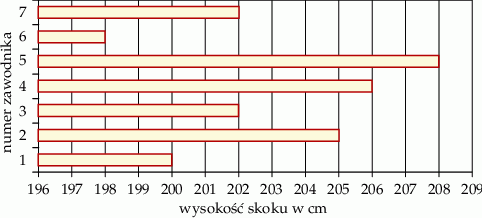
Ilu zawodników uzyskało wynik wyższy od średniej arytmetycznej wyników wszystkich uczestników finału tego konkursu?
A) 2 B) 3 C) 4 D) 5
Na diagramie przedstawiono wzrost (w centymetrach) ośmiu koszykarzy.
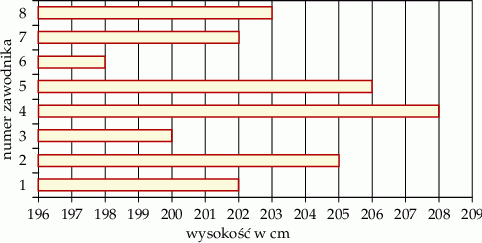
Ilu z tych zawodników ma wzrost mniejszy niż średni wzrost wszystkich zawodników przedstawionych na diagramie?
A) 2 B) 3 C) 4 D) 5

