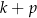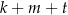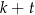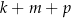Podatek od dochodów za rok 2016 w Polsce był obliczany według sposobów przedstawionych w poniższej tabeli.
| Podstawa obliczenia podatku | Sposób obliczenia podatku |
| kwota mniejsza lub równa 85 528 zł | 18% podstawy obliczenia podatku pomniejszone o 556,02 zł |
| kwota większa niż 85 528 zł | 14 839,02 zł plus 32% nadwyżki ponad 85 528 zł |
W 2016 roku podstawa obliczenia podatku dla pana Jana wyniosła 84 500 zł. Wysokość podatku (w zł) od dochodu pana Jana opisuje wyrażenie A/B.
A) 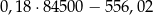 B)
B) 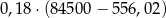
W 2016 roku podstawa obliczenia podatku dla pani Zofii wyniosła 97 300 zł. Wysokość podatku (w zł) od dochodu pani Zofii opisuje wyrażenie C/D.
C) 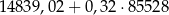 D)
D) 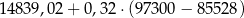

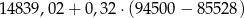
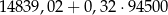
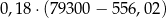
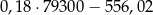
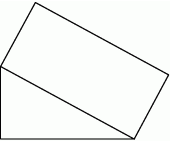
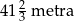
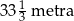
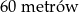
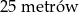
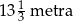
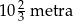
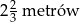
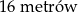
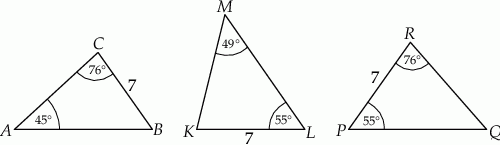
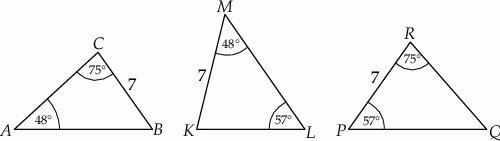
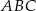 jest przystający do trójkąta
jest przystający do trójkąta 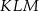 .
.  jest przystający do trójkąta
jest przystający do trójkąta  .
.  jest przystający do trójkąta
jest przystający do trójkąta  .
. 
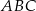 jest przystający do trójkąta
jest przystający do trójkąta 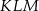 .
. 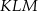 jest przystający do trójkąta
jest przystający do trójkąta 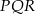 .
.  jest przystający do trójkąta
jest przystający do trójkąta  .
.  . Wynik zaokrąglij do pełnych centymetrów.
. Wynik zaokrąglij do pełnych centymetrów. 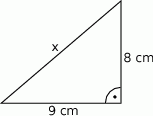
 . Wynik zaokrąglij do pełnych centymetrów.
. Wynik zaokrąglij do pełnych centymetrów. 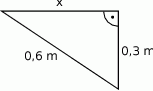
 . Wynik zaokrąglij do pełnych centymetrów.
. Wynik zaokrąglij do pełnych centymetrów. 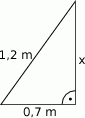
 . Wynik zaokrąglij do pełnych centymetrów.
. Wynik zaokrąglij do pełnych centymetrów. 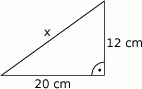
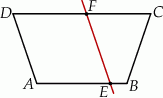
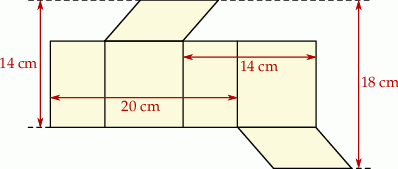
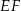 dzieli trapez równoramienny
dzieli trapez równoramienny 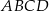 na romb
na romb 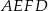 o obwodzie 52 cm i trapez
o obwodzie 52 cm i trapez 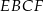 o obwodzie o 13 cm mniejszym od obwodu rombu
o obwodzie o 13 cm mniejszym od obwodu rombu 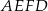 .
. 
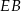 i
i 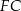 jest równa
jest równa 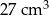 usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe
usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe 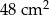
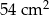
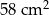
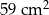
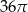 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa 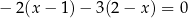 jest liczba
jest liczba 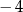
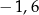
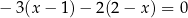 jest liczba
jest liczba 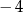
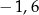
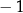
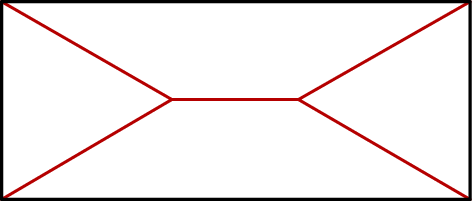
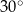 , to powstałe trójkąty byłyby równoboczne.
, to powstałe trójkąty byłyby równoboczne. 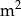 ) pomalowanej farbą z tego pojemnika.
) pomalowanej farbą z tego pojemnika. 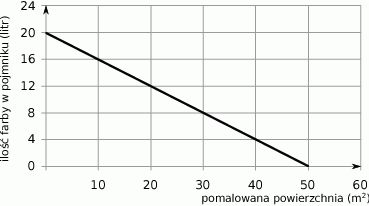
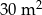 ściany?
ściany? 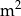 ) pomalowanej farbą z tego pojemnika.
) pomalowanej farbą z tego pojemnika. 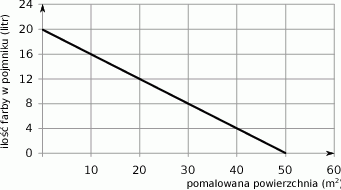
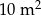 ściany?
ściany? 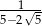 jest liczba:
jest liczba: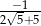
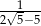
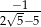
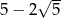
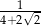 jest liczba
jest liczba 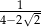
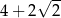
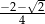
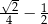
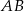 trójkąta
trójkąta 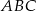 przecina bok
przecina bok 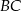 w punkcie
w punkcie 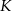 , przy czym odcinek
, przy czym odcinek 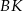 ma długość 5. Jaką długość ma odcinek
ma długość 5. Jaką długość ma odcinek 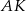 ?
? 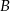 i
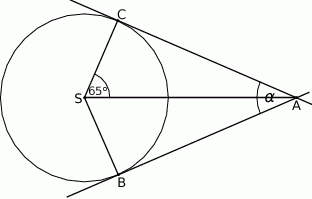
i 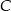 okręgu poprowadzono styczne, które przecięły się w punkcie
okręgu poprowadzono styczne, które przecięły się w punkcie 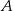 .
. 
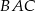 jeżeli
jeżeli 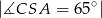 .
. 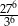 jest równa A/B.
jest równa A/B.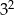
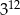
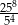 jest równa C/D.
jest równa C/D.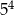
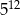
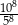 jest równy A/B.
jest równy A/B.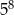
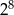
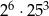 jest równy C/D.
jest równy C/D.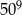
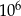
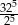 jest równa A/B.
jest równa A/B.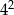
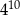
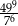 jest równa C/D.
jest równa C/D.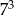
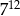
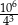 jest równy A/B.
jest równy A/B.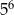
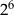
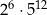 jest równy C/D.
jest równy C/D.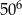
 .
.