W trakcie kontroli jakości basenu rekreacyjnego napełniono go całkowicie wodą. Po pewnym czasie w basenie wykryto usterkę i częściowo go opróżniono. Następnie usterkę usunięto i basen ponownie napełniono wodą. Na zakończenie kontroli basen całkowicie opróżniono z wody.
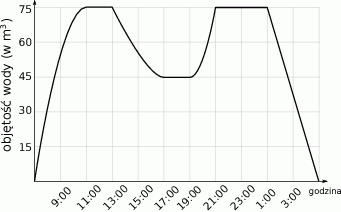
Na wykresie przedstawiono jak zmieniała się w czasie kontroli objętość wody w basenie.
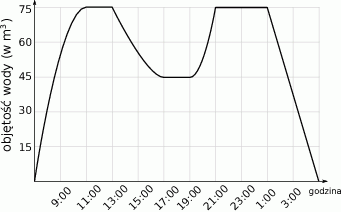
Ile wody spuszczono z basenu po wykryciu usterki?
A)
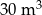 B)
B) 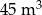 C)
C) 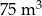 D)
D) 

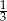 objętości wody usunięto w ciągu
objętości wody usunięto w ciągu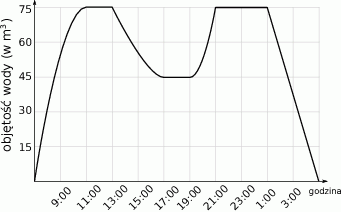
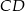 prostokąta
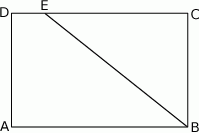
prostokąta 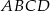 o bokach długości 12 cm i 20 cm wybrano punkt
o bokach długości 12 cm i 20 cm wybrano punkt 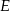 w ten sposób, że pole czworokąta
w ten sposób, że pole czworokąta 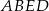 jest równe
jest równe 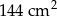 .
. 
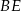 jest równa
jest równa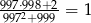 .
. 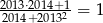 .
. 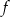 . Które zdanie jest prawdziwe?
. Które zdanie jest prawdziwe? 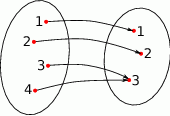
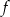 ma cztery argumenty.
ma cztery argumenty.  ma cztery różne wartości
ma cztery różne wartości  przyjmuje dwie wartości 3 i 4.
przyjmuje dwie wartości 3 i 4.  . Które zdanie jest prawdziwe?
. Które zdanie jest prawdziwe? 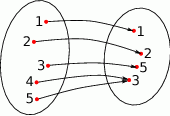
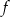 ma cztery argumenty.
ma cztery argumenty. 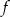 ma cztery różne wartości
ma cztery różne wartości 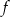 przyjmuje dwie wartości 4 i 5.
przyjmuje dwie wartości 4 i 5. 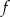 . Które zdanie jest prawdziwe?
. Które zdanie jest prawdziwe? 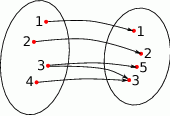
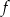 ma cztery argumenty.
ma cztery argumenty. 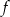 ma cztery różne wartości
ma cztery różne wartości 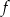 przyjmuje dwie wartości 3 i 5.
przyjmuje dwie wartości 3 i 5. 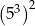 .
. 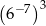 .
. 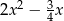 dla
dla 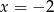 jest liczba:
jest liczba: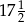
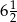
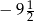
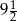
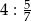 .
. 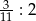 .
. 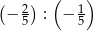 .
. 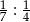 .
. 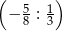 .
. 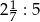 .
. 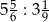 .
. 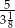 .
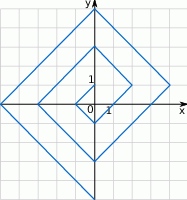
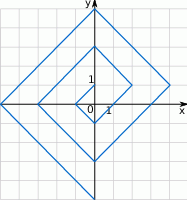
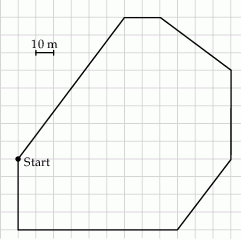
.  budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość
budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 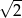 .
. 
 jest liczbą parzystą, to odcinek o numerze
jest liczbą parzystą, to odcinek o numerze  jest równoległydo odcinka o numerze 3.
jest równoległydo odcinka o numerze 3. jest liczbą nieparzystą, to długość odcinka o numerze
jest liczbą nieparzystą, to długość odcinka o numerze  jest równa
jest równa 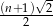 .
.  budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość
budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 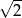 .
. 
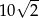 .
.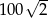 .
. 
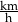 .
. 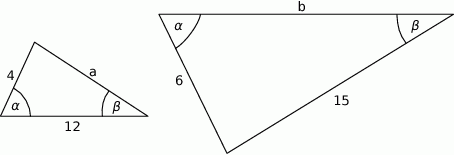
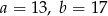
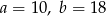
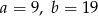
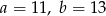
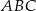 i
i 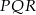 są podobne. Bok
są podobne. Bok 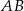 trójkąta
trójkąta 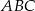 ma długość
ma długość 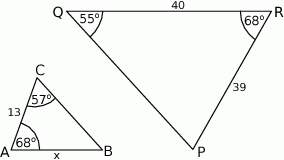
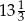
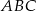 i
i 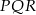 są podobne. Bok
są podobne. Bok 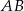 trójkąta
trójkąta 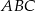 ma długość
ma długość 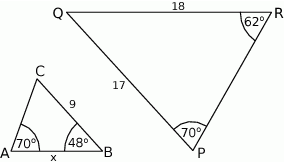
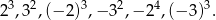
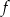 przyporządkowuje każdej liczbie naturalnej większej od 1 sumę jej cyfr. Liczba
przyporządkowuje każdej liczbie naturalnej większej od 1 sumę jej cyfr. Liczba  dla której prawdziwa jest równość
dla której prawdziwa jest równość 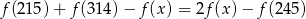
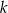 jest sumą liczb 323 i 160. Czy liczba
jest sumą liczb 323 i 160. Czy liczba 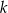 jest podzielna przez 3?
jest podzielna przez 3? 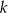 jest 3.
jest 3. 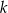 jest różnicą liczb 1423 i 1130. Czy liczba
jest różnicą liczb 1423 i 1130. Czy liczba 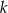 jest podzielna przez 3?
jest podzielna przez 3? 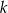 jest 3.
jest 3. 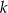 nie jest liczbą podzielną przez 3.
nie jest liczbą podzielną przez 3. 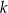 jest sumą liczb 243 i 162. Czy liczba
jest sumą liczb 243 i 162. Czy liczba 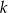 jest podzielna przez 81?
jest podzielna przez 81? 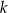 nie jest liczbą podzielną przez 81.
nie jest liczbą podzielną przez 81. 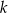 jest liczbą podzielną przez 81.
jest liczbą podzielną przez 81. 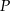 jest punktem przecięcia się wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt
jest punktem przecięcia się wysokości trójkąta równobocznego. Jakie pole ma ten trójkąt, jeśli odcinek łączący punkt 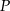 z wierzchołkiem trójkąta ma długość
z wierzchołkiem trójkąta ma długość 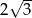 ?
? 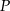 jest punktem przecięcia wysokości trójkąta równobocznego. Jaki obwód ma ten trójkąt jeśli odległość punktu
jest punktem przecięcia wysokości trójkąta równobocznego. Jaki obwód ma ten trójkąt jeśli odległość punktu 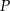 od jego boków jest równa
od jego boków jest równa 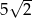 ?
? 