Dane są wierzchołki trójkąta 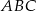 :
: 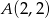 ,
, 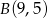 i
i 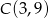 . Z wierzchołka
. Z wierzchołka 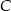 poprowadzono wysokość tego trójkąta, która przecina bok
poprowadzono wysokość tego trójkąta, która przecina bok 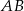 w punkcie
w punkcie 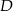 . Wyznacz równanie prostej przechodzącej przez punkt
. Wyznacz równanie prostej przechodzącej przez punkt 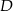 i równoległej do boku
i równoległej do boku 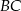 .
.
/Szkoła średnia/Geometria/Geometria analityczna
W kartezjańskim układzie współrzędnych 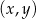 punkt
punkt 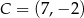 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 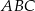 . Prosta
. Prosta 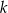 o równaniu
o równaniu 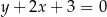 zawiera dwusieczną kąta
zawiera dwusieczną kąta 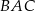 tego trójkąta. Okrąg
tego trójkąta. Okrąg 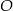 o równaniu
o równaniu 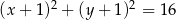 jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków
jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków 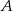 i
i 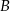 trójkąta
trójkąta 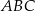 .
.
Napisz równanie okręgu, którego środek należy do osi 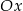 , i który przechodzi przez punkty
, i który przechodzi przez punkty 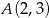 i
i 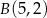 .
.
Napisz równanie okręgu, którego środek leży na prostej 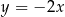 , i który przechodzi przez punkty
, i który przechodzi przez punkty 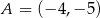 i
i 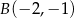 .
.
Wyznacz równanie okręgu przechodzącego przez punkty 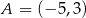 i
i 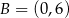 , którego środek leży na prostej o równaniu
, którego środek leży na prostej o równaniu 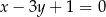 .
.
Wyznacz odległość punktu 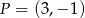 od prostej o równaniu
od prostej o równaniu 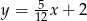 .
.
Wierzchołkami trójkąta 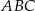 są punkty
są punkty 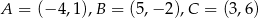 . Oblicz długość środkowej
. Oblicz długość środkowej 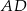 .
.
Wierzchołkami trójkąta 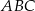 są punkty
są punkty 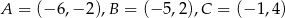 . Oblicz długość środkowej
. Oblicz długość środkowej 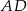 .
.
Dana jest parabola o równaniu 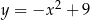 . Na tej paraboli leży punkt
. Na tej paraboli leży punkt 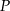 o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie
o dodatnich współrzędnych. Wyznacz współrzędne tego punktu tak, by styczna do paraboli w punkcie 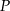 ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu.
ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu.
Dana jest funkcja 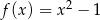 określona dla
określona dla 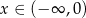 . W jakim punkcie wykresu tej funkcji należy poprowadzić styczną tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole? Oblicz to pole.
. W jakim punkcie wykresu tej funkcji należy poprowadzić styczną tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole? Oblicz to pole.
Do okręgów o równaniach 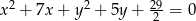 i
i 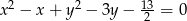 poprowadzono wspólną styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
poprowadzono wspólną styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
W trapezie 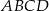 , w którym
, w którym 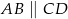 , dane są wierzchołki
, dane są wierzchołki 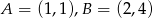 oraz punkt przecięcia przekątnych
oraz punkt przecięcia przekątnych 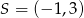 . Pole trapezu jest równe 36.
. Pole trapezu jest równe 36.
- Oblicz długość podstawy
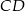 .
. - Wyznacz współrzędne wierzchołków
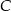 i
i 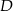 .
.
Dany jest prostokąt o wierzchołkach 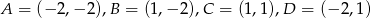 . Wyznacz wszystkie wartości współczynnika
. Wyznacz wszystkie wartości współczynnika 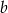 , dla których prosta o równaniu
, dla których prosta o równaniu 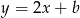 ma co najmniej jeden punkt wspólny z prostokątem
ma co najmniej jeden punkt wspólny z prostokątem 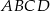 .
.
Prosta przechodząca przez punkty 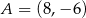 i
i 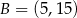 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 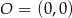 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 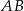 .
.
Prosta przechodząca przez punkty 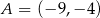 i
i 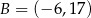 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 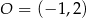 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 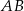 .
.
Punkty 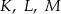 są środkami boków
są środkami boków 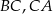 i
i 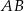 trójkąta
trójkąta 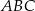 . Wykaż, że
. Wykaż, że
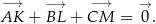
W kartezjańskim układzie współrzędnych dany jest romb 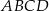 , którego bok
, którego bok 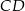 i przekątna
i przekątna 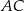 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 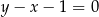 i
i 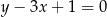 odpowiednio. Promień okręgu wpisanego w romb
odpowiednio. Promień okręgu wpisanego w romb 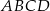 jest równy
jest równy 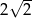 , a środek tego okręgu leży poniżej osi
, a środek tego okręgu leży poniżej osi 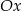 . Oblicz współrzędne punktu styczności okręgu wpisanego w romb
. Oblicz współrzędne punktu styczności okręgu wpisanego w romb 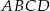 z jego bokiem
z jego bokiem 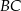 .
.
Zapisz równanie prostej przechodzącej przez punkt 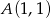 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 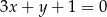 .
.
Zapisz równanie prostej przechodzącej przez punkt 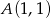 i równoległej do prostej danej równaniem
i równoległej do prostej danej równaniem 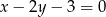 .
.
Dany jest trójkąt 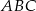 o wierzchołkach
o wierzchołkach 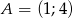 ,
, 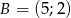 ,
, 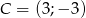 .
.
- Napisz równanie wysokości opuszczonej z wierzchołka
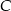 na bok
na bok 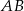 .
. - Napisz równanie środkowej boku
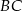 .
. - Napisz równanie symetralnej boku
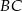 .
. - Oblicz obwód i pole tego trójkąta.
Wyznacz równanie okręgu, który jest symetryczny do okręgu o równaniu
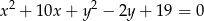
względem prostej 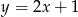 .
.
Wiadomo, że okrąg jest styczny do prostej o równaniu 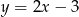 w punkcie
w punkcie 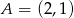 i styczny do prostej o równaniu
i styczny do prostej o równaniu 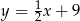 w punkcie
w punkcie 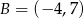 . Oblicz promień tego okręgu.
. Oblicz promień tego okręgu.
W kartezjańskim układzie współrzędnych 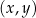 prosta
prosta 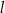 o równaniu
o równaniu 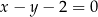 przecina parabolę o równaniu
przecina parabolę o równaniu 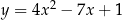 w punktach
w punktach 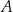 oraz
oraz 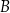 . Odcinek
. Odcinek 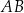 jest średnicą okręgu
jest średnicą okręgu 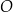 . Punkt
. Punkt 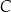 leży na okręgu
leży na okręgu 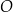 nad prostą
nad prostą 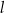 , a kąt
, a kąt 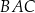 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 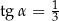 (zobacz rysunek).
(zobacz rysunek).
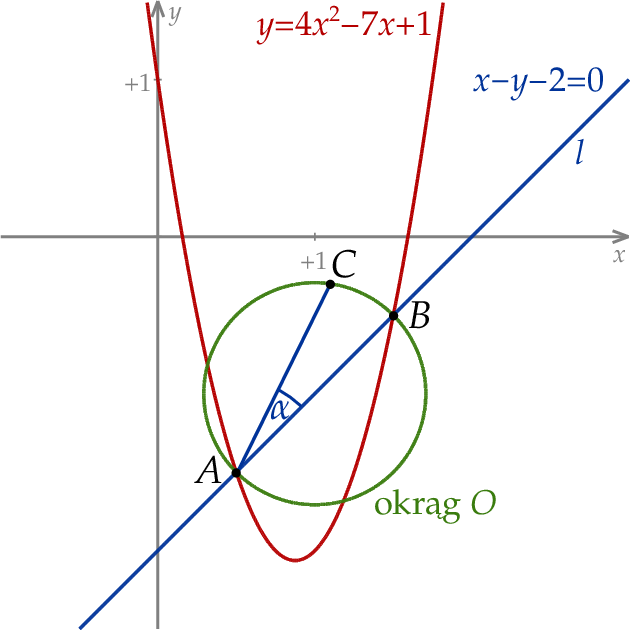
Oblicz współrzędne punktu 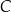 .
.
W kartezjańskim układzie współrzędnych 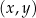 prosta
prosta 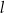 o równaniu
o równaniu 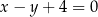 przecina parabolę o równaniu
przecina parabolę o równaniu 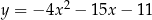 w punktach
w punktach 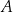 oraz
oraz 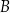 . Odcinek
. Odcinek 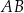 jest średnicą okręgu
jest średnicą okręgu 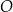 . Punkt
. Punkt 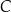 leży na okręgu
leży na okręgu 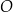 poniżej prostej
poniżej prostej 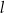 , a kąt
, a kąt 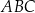 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 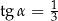 (zobacz rysunek).
(zobacz rysunek).
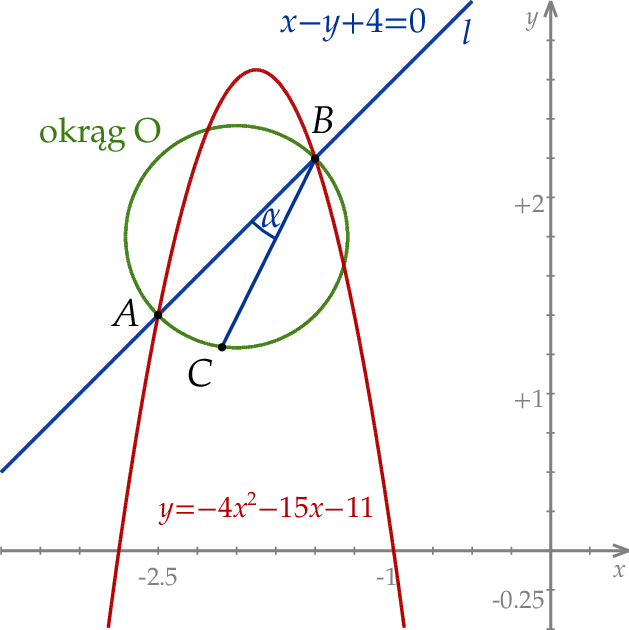
Oblicz współrzędne punktu 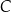 .
.
Wykaż, że trójkąt 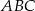 o wierzchołkach
o wierzchołkach 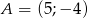 ,
, 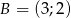 ,
, 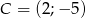 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt 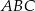 o wierzchołkach
o wierzchołkach 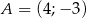 ,
, 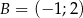 ,
, 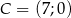 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt o wierzchołkach 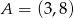 ,
, 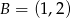 ,
, 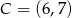 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt 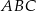 o wierzchołkach
o wierzchołkach 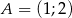 ,
, 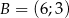 ,
, 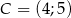 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt 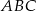 o wierzchołkach
o wierzchołkach 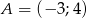 ,
, 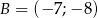 ,
, 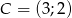 jest prostokątny.
jest prostokątny.
Wykaż, że trójkąt o wierzchołkach 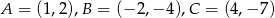 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Punkt 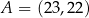 jest wierzchołkiem trójkąta prostokątnego o polu
jest wierzchołkiem trójkąta prostokątnego o polu 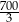 . Prosta
. Prosta 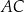 zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną
zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną 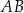 ma równanie
ma równanie 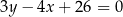 . Środek okręgu wpisanego w trójkąt
. Środek okręgu wpisanego w trójkąt 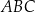 ma współrzędne
ma współrzędne 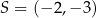 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 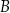 i
i 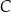 tego trójkąta.
tego trójkąta.
Wyznacz współrzędne środka okręgu opisanego na kwadracie, którego jeden z boków jest zawarty w prostej o równaniu 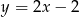 , a punkt
, a punkt 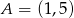 jest jego wierzchołkiem. Rozważ wszystkie przypadki.
jest jego wierzchołkiem. Rozważ wszystkie przypadki.

