W kartezjańskim układzie współrzędnych 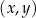 prosta o równaniu
prosta o równaniu 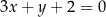 przecina parabolę o równaniu
przecina parabolę o równaniu 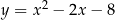 w punktach
w punktach 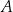 oraz
oraz 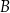 , które są kolejnymi wierzchołkami równoległoboku
, które są kolejnymi wierzchołkami równoległoboku 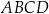 . Wierzchołek
. Wierzchołek 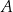 ma pierwszą współrzędną ujemną. Wierzchołek
ma pierwszą współrzędną ujemną. Wierzchołek 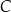 leży na prostej o równaniu
leży na prostej o równaniu 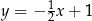 i ma pierwszą współrzędną dodatnią. Odległość punktu
i ma pierwszą współrzędną dodatnią. Odległość punktu 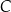 od prostej zawierającej bok
od prostej zawierającej bok 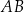 równoległoboku jest równa
równoległoboku jest równa 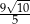 . Oblicz długość boku
. Oblicz długość boku 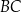 tego równoległoboku.
tego równoległoboku.
/Szkoła średnia/Geometria/Geometria analityczna
Punkty 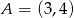 ,
, 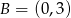 i
i 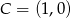 należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.
należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.
Punkty 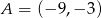 i
i 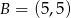 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 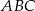 , w którym
, w którym 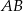 jest przeciwprostokątną. Wyznacz współrzędne wierzchołka
jest przeciwprostokątną. Wyznacz współrzędne wierzchołka 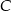 wiedząc, że leży on na osi
wiedząc, że leży on na osi 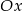 .
.
Punkty 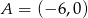 i
i 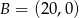 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 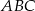 o przeciwprostokątnej
o przeciwprostokątnej 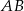 . Wierzchołek
. Wierzchołek 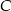 leży na prostej o równaniu
leży na prostej o równaniu 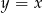 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 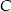 .
.
Punkty 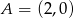 i
i 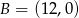 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 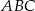 o przeciwprostokątnej
o przeciwprostokątnej 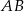 . Wierzchołek
. Wierzchołek 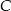 leży na prostej o równaniu
leży na prostej o równaniu 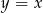 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 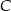 .
.
Proste 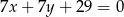 i
i 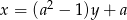 przecinają się pod kątem
przecinają się pod kątem 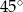 . Wyznacz liczbę
. Wyznacz liczbę  .
.
O ile procent pole koła o promieniu długości 8 jest większe od pola koła wyznaczonego przez okrąg o równaniu 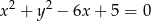 .
.
Dane są okręgi o równaniach 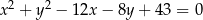 i
i 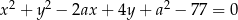 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Dane są okręgi o równaniach 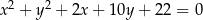 i
i 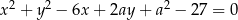 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Środek 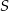 okręgu
okręgu 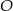 należy do prostej
należy do prostej 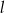 o równaniu
o równaniu 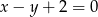 . Punkty
. Punkty 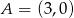 i
i 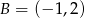 należą do tego okręgu.
należą do tego okręgu.
- Wyznacz równanie okręgu
 .
. - Wyznacz współrzędne takiego punktu
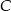 należącego do okręgu
należącego do okręgu 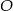 , że
, że 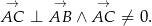
- Wyznacz równania stycznych
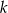 i
i 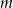 do okręgu
do okręgu 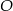 takich, że
takich, że 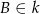 i
i 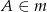 oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
Wyznacz odległość punktu 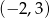 od prostej o równaniu
od prostej o równaniu 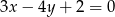 .
.
Dla jakich wartości parametru 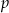 proste
proste 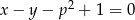 i
i 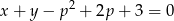 przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach
przecinają się w punkcie należącym do wnętrza prostokąta o wierzchołkach 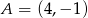 ,
, 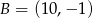 ,
, 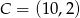 ,
, 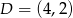 ?
?
Przekątne deltoidu 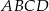 przecinają się w punkcie
przecinają się w punkcie 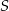 , który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie
, który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie 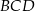 jeżeli okręgi opisane na trójkątach
jeżeli okręgi opisane na trójkątach 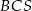 i
i 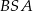 mają odpowiednio równania
mają odpowiednio równania 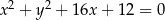 i
i 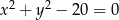 .
.
Określ wzajemne położenie prostej 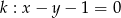 i okręgu o równaniu
i okręgu o równaniu 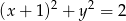 .
.
Wykaż, że dla dowolnych punktów płaszczyzny 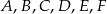 spełniona jest równość.
spełniona jest równość.
Okrąg  o środku w punkcie
o środku w punkcie  jest określony równaniem
jest określony równaniem 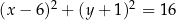 . Okrąg
. Okrąg 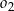 ma środek w punkcie
ma środek w punkcie 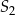 takim, że
takim, że ![−→ S 1S2 = [− 4,4]](https://img.zadania.info/zad/9553446/HzadT5x.png) . Promienie tych okręgów są sobie równe. Figura
. Promienie tych okręgów są sobie równe. Figura 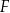 składa się z dwóch okręgów:
składa się z dwóch okręgów: 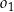 oraz
oraz 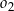 . Punkty
. Punkty 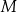 i
i 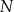 są punktami przecięcia figury
są punktami przecięcia figury 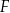 z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt
z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt 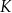 , leżący na jednej z osi symetrii figury
, leżący na jednej z osi symetrii figury 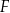 , taki, że pole trójkąta
, taki, że pole trójkąta 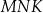 jest równe 40.
jest równe 40.
Wierzchołki trójkąta 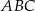 mają współrzędne:
mają współrzędne: 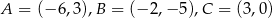 . Okrąg
. Okrąg  jest styczny do prostej
jest styczny do prostej 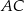 , a jego środek jest punktem przecięcia się wysokości trójkąta
, a jego środek jest punktem przecięcia się wysokości trójkąta 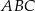 . Okrąg
. Okrąg  przecina prostą
przecina prostą 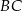 w punkcie
w punkcie 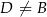 . Oblicz iloraz
. Oblicz iloraz 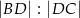 .
.
Dany jest okrąg 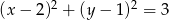 . Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
. Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
Wierzchołki trójkąta 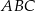 mają współrzędne:
mają współrzędne: 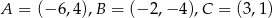 . Napisz równanie okręgu, który jest styczny do prostej
. Napisz równanie okręgu, który jest styczny do prostej  , a jego środek jest punktem przecięcia się wysokości trójkąta
, a jego środek jest punktem przecięcia się wysokości trójkąta  .
.
Oblicz dla jakich wartości parametrów 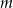 i
i  proste o równaniach:
proste o równaniach: 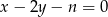 i
i 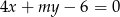 są dwiema różnymi prostymi równoległymi.
są dwiema różnymi prostymi równoległymi.
Boki 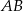 i
i 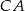 trójkąta
trójkąta 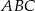 są zawarte w prostych
są zawarte w prostych 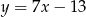 i
i 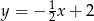 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 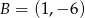 i
i 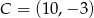 . Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok
. Oblicz współrzędne spodka wysokości tego trójkąta opuszczonej na bok 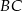 .
.
Punkt 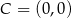 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 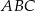 , którego wierzchołek
, którego wierzchołek 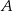 leży na osi
leży na osi 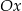 , a wierzchołek
, a wierzchołek 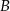 na osi
na osi 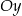 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 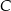 przecina przeciwprostokątną
przecina przeciwprostokątną 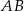 w punkcie
w punkcie 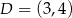 .
.
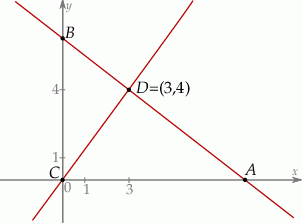
Oblicz współrzędne wierzchołków  i
i  tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej  .
.
Punkt 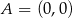 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 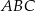 , którego wierzchołek
, którego wierzchołek 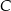 leży na osi
leży na osi 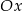 , a wierzchołek
, a wierzchołek 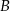 na osi
na osi 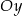 układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka
układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 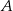 przecina przeciwprostokątną
przecina przeciwprostokątną 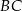 w punkcie
w punkcie 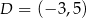 .
.
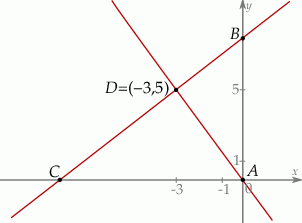
Oblicz współrzędne wierzchołków  i
i  tego trójkąta oraz długość przeciwprostokątnej
tego trójkąta oraz długość przeciwprostokątnej 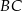 .
.
W układzie współrzędnych narysuj okrąg o równaniu 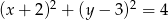 oraz zaznacz punkt
oraz zaznacz punkt 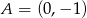 . Prosta o równaniu
. Prosta o równaniu 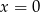 jest jedną ze stycznych do tego okręgu przechodzących przez punkt
jest jedną ze stycznych do tego okręgu przechodzących przez punkt 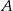 . Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt
. Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt 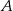 .
.

