Dla jakich wartości parametru 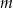 równanie
równanie 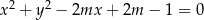 opisuje okrąg?
opisuje okrąg?
- Podaj współrzędne środka i długość promienia okręgu.
- Dla jakich wartości parametru
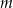 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 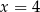 ?
?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla jakich wartości parametru 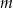 równanie
równanie 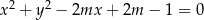 opisuje okrąg?
opisuje okrąg?
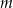 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 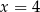 ?
?Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 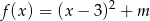 , gdzie
, gdzie 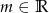 – parametr.
– parametr.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 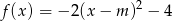 , gdzie
, gdzie 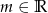 – parametr.
– parametr.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 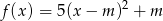 , gdzie
, gdzie 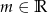 – parametr.
– parametr.
Wyznacz zbiór wszystkich punktów płaszczyzny, jaki tworzą wierzchołki parabol o równaniu 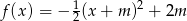 , gdzie
, gdzie 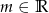 – parametr.
– parametr.
W trójkącie 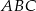 , gdzie
, gdzie 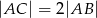 dane są
dane są 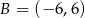 i
i 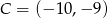 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 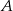 , jeżeli leży on na prostej
, jeżeli leży on na prostej 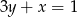 .
.
W kartezjańskim układzie współrzędnych 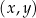 dane są punkty
dane są punkty 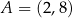 oraz
oraz 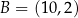 . Symetralna odcinka
. Symetralna odcinka 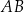 przecina oś
przecina oś 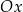 układu współrzędnych w punkcie
układu współrzędnych w punkcie 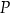 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 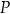 oraz długość odcinka
oraz długość odcinka 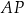 .
.
Punkty 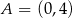 i
i 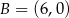 są końcami odcinka
są końcami odcinka 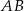 . Prosta
. Prosta 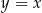 przecina odcinek
przecina odcinek 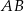 w punkcie
w punkcie 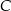 . Oblicz stosunek
. Oblicz stosunek 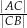 .
.
Punkty 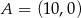 i
i 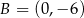 są końcami odcinka
są końcami odcinka 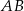 . Prosta
. Prosta 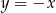 przecina odcinek
przecina odcinek 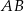 w punkcie
w punkcie 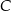 . Oblicz stosunek
. Oblicz stosunek 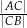 .
.
Udowodnij, że jeżeli punkt 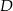 jest środkiem ciężkości trójkąta, to
jest środkiem ciężkości trójkąta, to 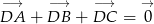 .
.
Dane są dwa przeciwległe wierzchołki kwadratu 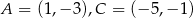 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
Dane są dwa przeciwległe wierzchołki kwadratu 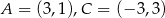 . Oblicz obwód tego kwadratu.
. Oblicz obwód tego kwadratu.
Wyznacz wartości funkcji trygonometrycznych kąta 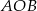 oraz jego miarę, jeżeli
oraz jego miarę, jeżeli 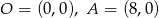 oraz
oraz
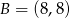
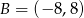
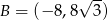
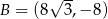
Punkty 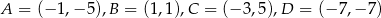 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Punkty 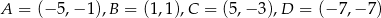 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Punkty 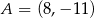 i
i 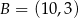 są końcami cięciwy okręgu o środku
są końcami cięciwy okręgu o środku 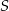 . Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt
. Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt 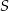 .
.
Znajdź równanie okręgu stycznego do prostej 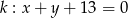 i do prostej
i do prostej 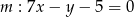 w punkcie
w punkcie 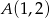 .
.
Dla dowolnej liczby 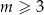 , prosta
, prosta 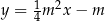 przecina hiperbolę
przecina hiperbolę 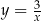 w punktach
w punktach 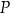 i
i 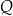 . Uzasadnij, że
. Uzasadnij, że 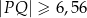 .
.
Określ wzajemne położenie prostych 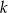 i
i 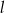 o równaniach
o równaniach
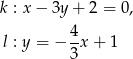
Współrzędne przeciwległych wierzchołków prostokąta 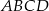 są równe
są równe 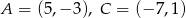 . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek
. Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek 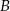 leży na prostej
leży na prostej 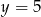 .
.
Prosta o równaniu 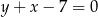 zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta
zawiera jedną z dwusiecznych kątów wewnętrznych trójkąta 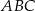 , w którym
, w którym 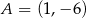 i
i 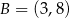 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
Dane są punkty 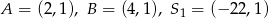 i
i 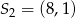 . Odcinek
. Odcinek 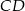 jest obrazem odcinka
jest obrazem odcinka 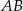 w jednokładności o skali dodatniej i środku
w jednokładności o skali dodatniej i środku 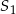 , jak i w jednokładności o skali ujemnej i środku
, jak i w jednokładności o skali ujemnej i środku 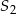 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 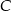 i
i 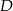 .
.
Dana jest prosta 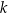 o równaniu
o równaniu 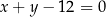 oraz punkt
oraz punkt 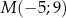 wyznacz na prostej
wyznacz na prostej  takie punkty
takie punkty 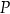 i
i 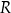 aby
aby 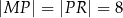 .
.
Znajdź zbiór środków wszystkich okręgów stycznych wewnętrznie do okręgu o równaniu 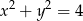 i stycznych do prostej o równaniu
i stycznych do prostej o równaniu 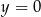 .
.
Punkty 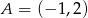 i
i 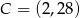 są wierzchołkami trójkąta równoramiennego, w którym
są wierzchołkami trójkąta równoramiennego, w którym 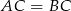 . Prosta zawierająca wysokość opuszczoną z wierzchołka
. Prosta zawierająca wysokość opuszczoną z wierzchołka 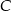 ma równanie
ma równanie 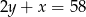 . Oblicz pole trójkąta
. Oblicz pole trójkąta 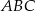 .
.
Punkty 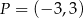 ,
, 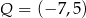 i
i 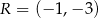 są środkami odpowiednio boków
są środkami odpowiednio boków 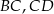 i
i 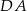 równoległoboku
równoległoboku 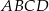 . Wyznacz współrzędne wierzchołków tego równoległoboku.
. Wyznacz współrzędne wierzchołków tego równoległoboku.
