W zbieżnym nieskończonym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 4, a różnica między trzecim i piątym wyrazem jest równa 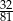 . Jaka jest suma wyrazów tego ciągu?
. Jaka jest suma wyrazów tego ciągu?
/Szkoła średnia/Ciągi/Szereg geometryczny/Liczenie sumy
Ciąg 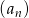 jest określony dla
jest określony dla 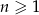 i spełnia warunki
i spełnia warunki
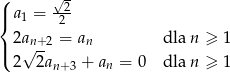
Oblicz granicę
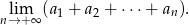
Dany jest okrąg 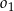 o promieniu
o promieniu  . Wewnątrz tego okręgu narysowano okrąg
. Wewnątrz tego okręgu narysowano okrąg 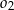 styczny wewnętrznie o średnicy
styczny wewnętrznie o średnicy  , wewnątrz okręgu
, wewnątrz okręgu 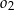 znów narysowano okrąg styczny wewnętrznie o średnicy
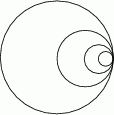
znów narysowano okrąg styczny wewnętrznie o średnicy 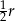 itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę długości wszystkich skonstruowanych w ten sposób okręgów.
itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę długości wszystkich skonstruowanych w ten sposób okręgów.
Suma czterech początkowych wyrazów ciągu 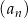 określonego dla
określonego dla 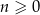 jest równa
jest równa 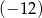 . Ponadto dla każdej liczby całkowitej
. Ponadto dla każdej liczby całkowitej 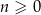 spełniony jest warunek
spełniony jest warunek 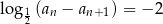 . Oblicz nieskończoną sumę
. Oblicz nieskończoną sumę
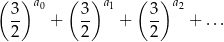
W trójkącie 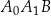 kąt
kąt 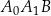 jest prosty,
jest prosty, 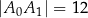 i
i 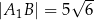 . Odcinek
. Odcinek 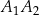 jest wysokością tego trójkąta, odcinek
jest wysokością tego trójkąta, odcinek 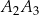 jest wysokością trójkąta
jest wysokością trójkąta 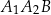 , odcinek
, odcinek 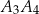 jest wysokością trójkąta
jest wysokością trójkąta 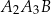 itd. Ogólnie, dla każdej liczby naturalnej
itd. Ogólnie, dla każdej liczby naturalnej 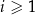 , odcinek
, odcinek 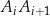 jest wysokością trójkąta
jest wysokością trójkąta 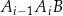
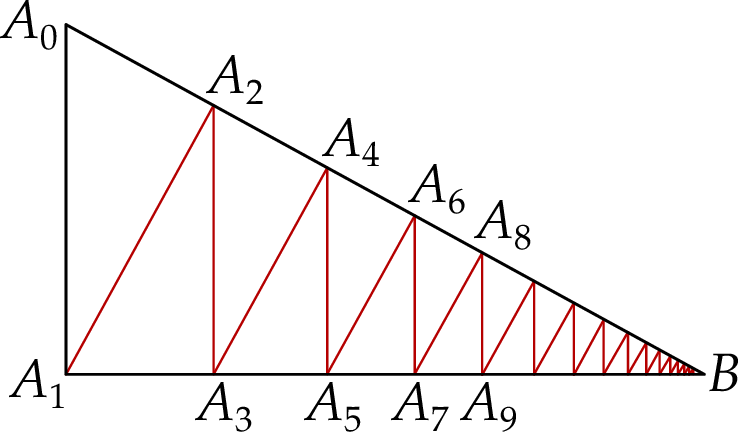
Oblicz długość nieskończonej łamanej 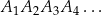 .
.
Oblicz sumę nieskończonego ciągu geometrycznego 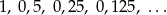
Dany jest nieskończony ciąg geometryczny
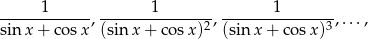
gdzie 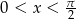 .
.
- Wykaż, że dany ciąg jest malejący.
- Wyznacz sumę
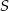 wszystkich wyrazów tego ciągu.
wszystkich wyrazów tego ciągu. - Wiedząc, że suma
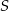 wszystkich wyrazów tego ciągu wynosi
wszystkich wyrazów tego ciągu wynosi 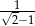 , oblicz
, oblicz  .
.
Oblicz sumę szeregu
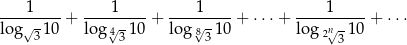
Niech 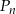 oznacza pole koła o promieniu
oznacza pole koła o promieniu 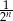 , dla
, dla 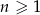 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 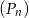 .
.
Niech 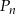 oznacza pole koła o promieniu
oznacza pole koła o promieniu 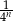 , dla
, dla 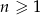 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 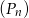 .
.
Niech 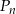 oznacza pole koła o promieniu
oznacza pole koła o promieniu 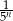 , dla
, dla 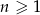 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 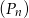 .
.
Niech 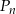 oznacza pole koła o promieniu
oznacza pole koła o promieniu 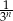 , dla
, dla 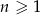 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 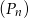 .
.

