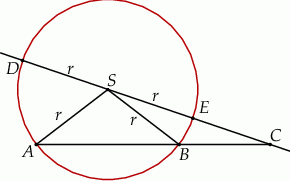
Dany jest okrąg o środku w punkcie  i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy  poza punkt
poza punkt  odłożono odcinek
odłożono odcinek 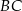 . Przez punkty
. Przez punkty 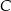 i
i 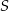 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 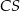 przecina dany okrąg w punktach
przecina dany okrąg w punktach 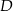 i
i 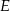 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 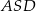 jest trzy razy większa od miary kąta
jest trzy razy większa od miary kąta 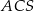 , to
, to 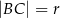 .
.

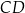 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie  . Uzasadnij, że jeśli
. Uzasadnij, że jeśli 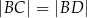 , to
, to 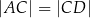 .
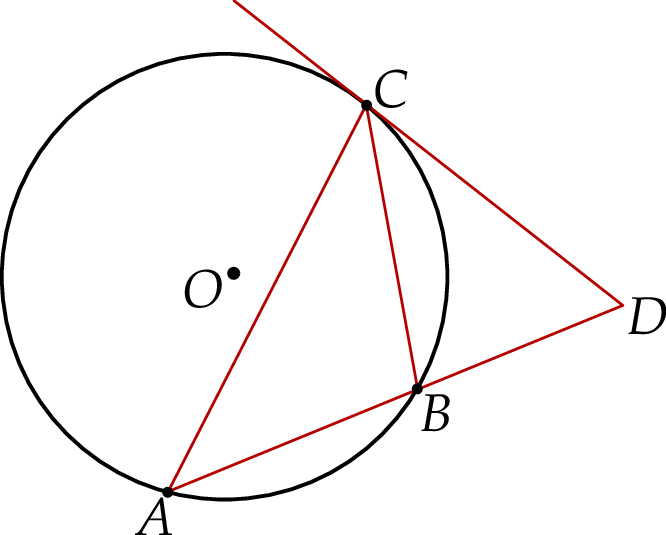
. 
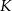 i
i 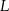 . Przez punkty
. Przez punkty 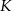 i
i 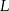 poprowadzono proste, które przecinają dane okręgi w punktach
poprowadzono proste, które przecinają dane okręgi w punktach 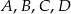 tak, jak pokazano to na poniższym rysunku. Wykaż, że
tak, jak pokazano to na poniższym rysunku. Wykaż, że 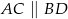 .
. 
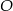 i średnicach odpowiednio
i średnicach odpowiednio  i
i 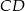 (punkty
(punkty 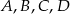 i
i  są współliniowe).
są współliniowe). 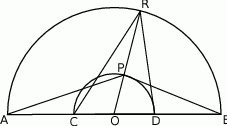
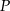 leży na wewnętrznym półokręgu, punkt
leży na wewnętrznym półokręgu, punkt 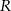 leży na zewnętrznym półokręgu, punkty
leży na zewnętrznym półokręgu, punkty 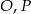 i
i 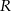 są współliniowe. Udowodnij, że
są współliniowe. Udowodnij, że 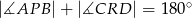 .
. 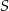 wybrano punkty
wybrano punkty 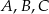 i
i 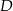 w ten sposób, że prosta
w ten sposób, że prosta 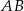 zawiera punkt
zawiera punkt 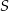 , a proste
, a proste 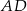 i
i 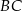 przecinają się w punkcie
przecinają się w punkcie 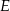 . Punkt
. Punkt 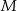 jest punktem wspólnym prostych
jest punktem wspólnym prostych 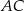 i
i 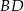 . Wykaż, że proste
. Wykaż, że proste 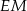 i
i 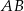 są prostopadłe.
są prostopadłe. 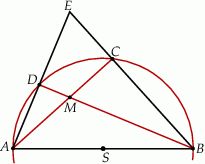
 , że
, że 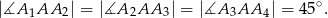
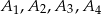 są wierzchołkami kwadratu.
są wierzchołkami kwadratu. 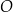 . Przez punkt
. Przez punkt 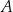 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 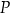 oraz
oraz 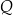 . Przez punkt
. Przez punkt 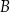 leżący na odcinku
leżący na odcinku 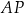 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie 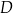 , która przecięła odcinek
, która przecięła odcinek  w punkcie
w punkcie 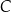 (zobacz rysunek).
(zobacz rysunek). 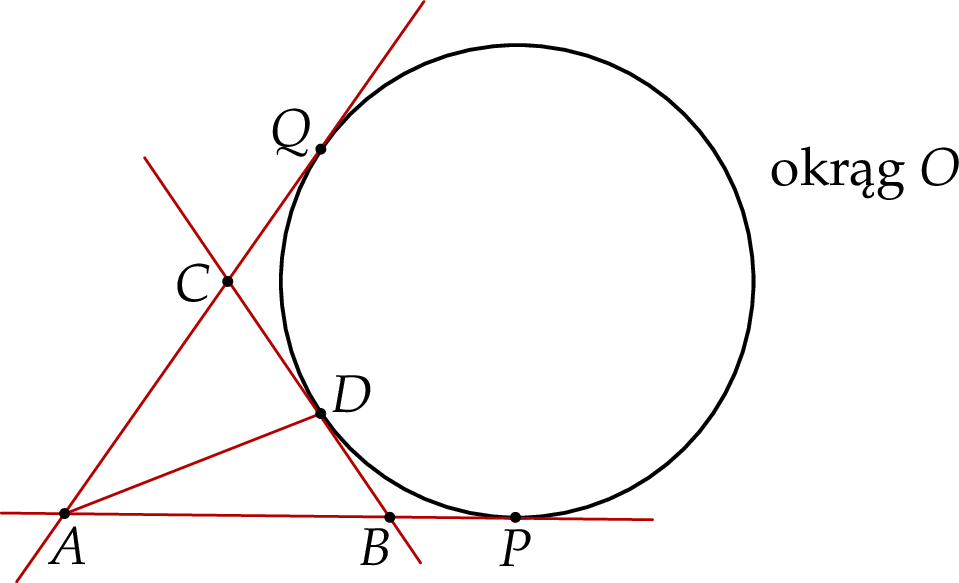
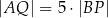 oraz
oraz 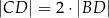 , to trójkąt
, to trójkąt 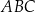 jest równoramienny.
jest równoramienny.  . Przez punkt
. Przez punkt 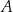 poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio –
poprowadzono dwie proste, które są styczne do tego okręgu w punktach – odpowiednio – 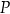 oraz
oraz 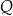 . Przez punkt
. Przez punkt 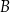 leżący na odcinku
leżący na odcinku 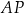 poprowadzono styczną do tego okręgu w punkcie
poprowadzono styczną do tego okręgu w punkcie  , która przecięła odcinek
, która przecięła odcinek  w punkcie
w punkcie  (zobacz rysunek).
(zobacz rysunek). 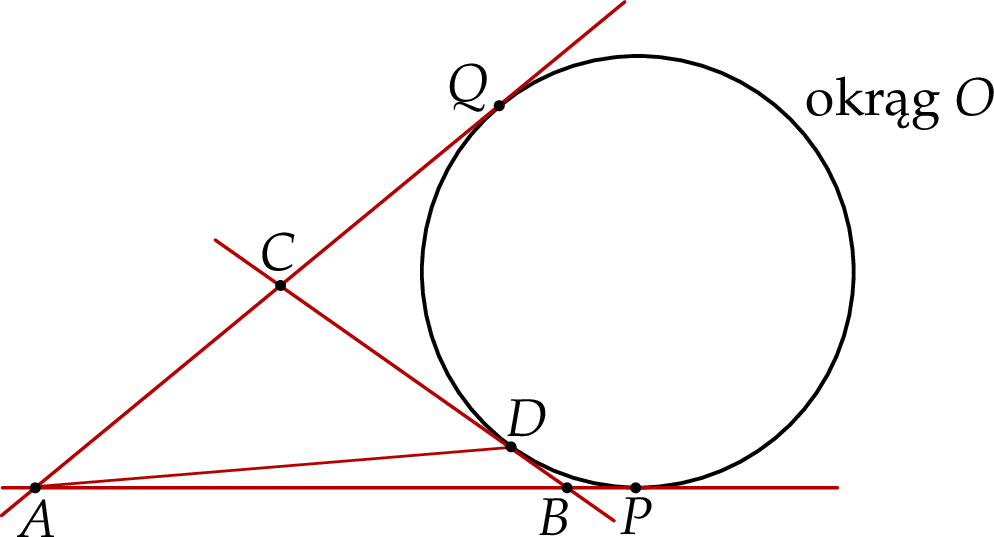
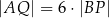 oraz
oraz 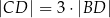 , to trójkąt
, to trójkąt 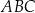 nie jest równoramienny.
nie jest równoramienny. 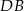 jest styczna do okręgu w punkcie
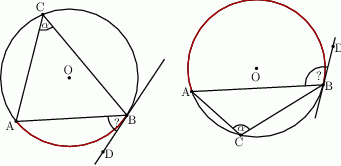
jest styczna do okręgu w punkcie 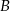 . Oblicz miarę zaznaczonego kąta
. Oblicz miarę zaznaczonego kąta 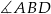 jeśli
jeśli 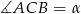 .
. 
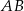 i cięciwa
i cięciwa 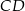 okręgu o środku
okręgu o środku 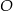 i promieniu
i promieniu  przecinają się w punkcie
przecinają się w punkcie 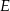 takim, że
takim, że 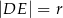 . Wykaż, że
. Wykaż, że 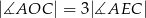 .
. 
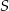 i promieniu
i promieniu  . Na przedłużeniu cięciwy
. Na przedłużeniu cięciwy 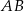 poza punkt
poza punkt 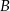 odłożono odcinek
odłożono odcinek 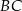 równy promieniowi danego okręgu. Przez punkty
równy promieniowi danego okręgu. Przez punkty 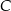 i
i 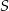 poprowadzono prostą. Prosta
poprowadzono prostą. Prosta 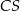 przecina dany okrąg w punktach
przecina dany okrąg w punktach 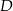 i
i 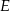 (zobacz rysunek). Wykaż, że jeżeli miara kąta
(zobacz rysunek). Wykaż, że jeżeli miara kąta 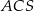 jest równa
jest równa  , to miara kąta
, to miara kąta 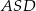 jest równa
jest równa 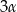 .
.