Dany jest ostrosłup prawidłowy czworokątny o krawędzi bocznej dwa razy dłuższej od krawędzi podstawy.
-
Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa.
-
Wyznacz długość krawędzi ostrosłupa, tak aby pole jego powierzchni bocznej wynosiło
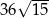 .
.

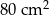 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 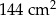 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.  .
. 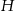 , a długość jego krawędzi podstawy jest równa
, a długość jego krawędzi podstawy jest równa  .
.  taki, że
taki, że 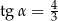 .
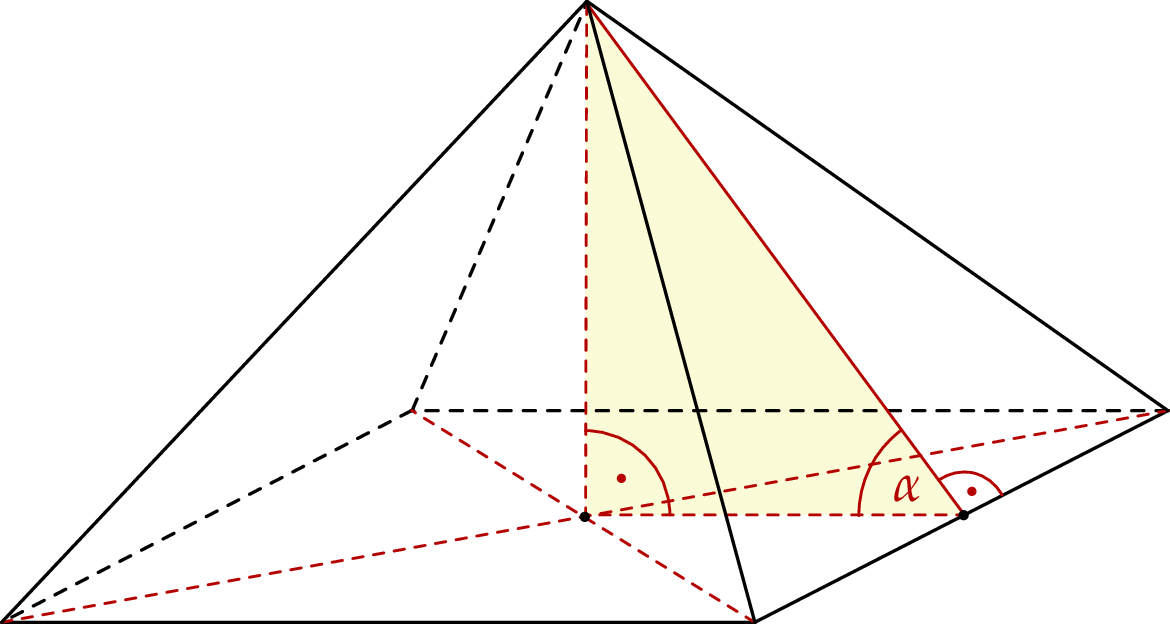
. 
 taki, że
taki, że 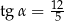 .
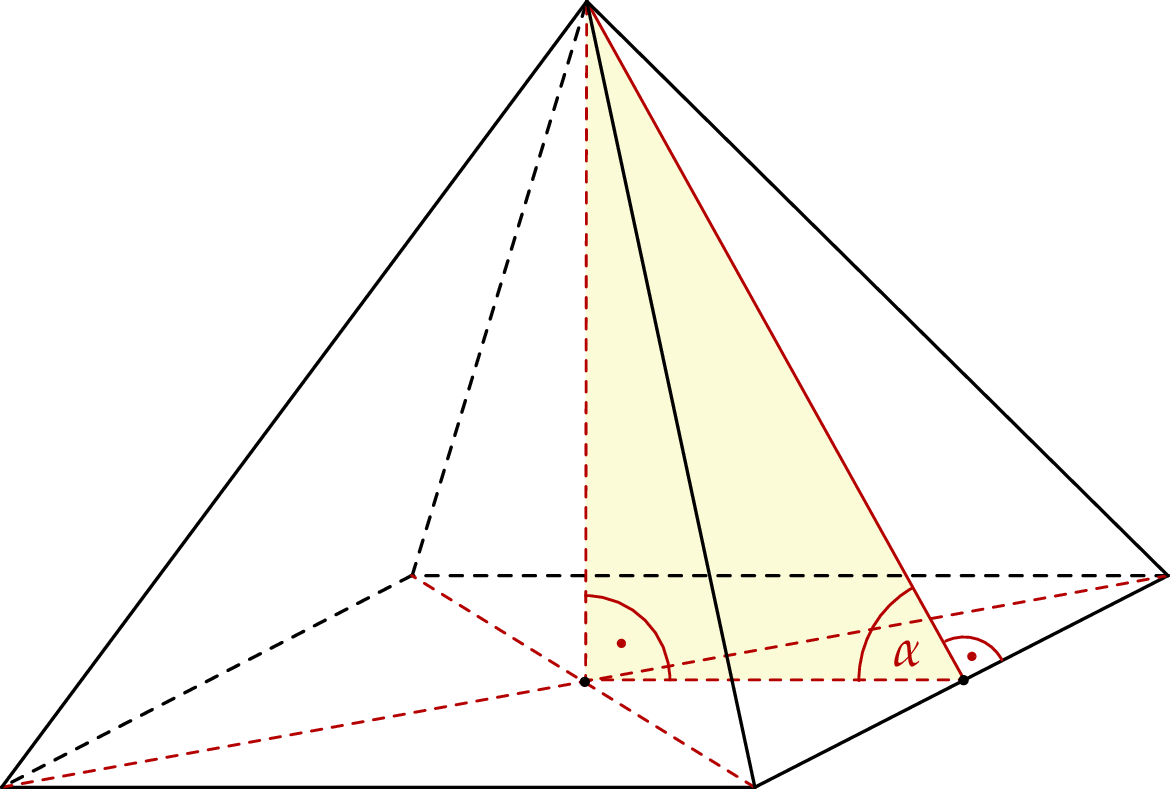
. 
 , a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się
, a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się 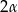 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa. 