W trójkącie 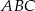 prowadzimy dwusieczną kąta
prowadzimy dwusieczną kąta 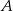 i przez punkt
i przez punkt 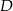 przecięcia się tej dwusiecznej z bokiem
przecięcia się tej dwusiecznej z bokiem 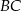 prowadzimy proste równoległe do boków
prowadzimy proste równoległe do boków 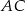 i
i 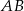 , które przecinają te boki odpowiednio w punktach
, które przecinają te boki odpowiednio w punktach 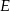 i
i 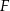 . Wykaż, że czworokąt
. Wykaż, że czworokąt 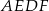 jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
/Szkoła podstawowa/Geometria/Trójkąt/Dowolny/Udowodnij...
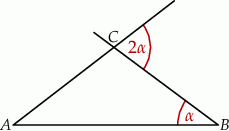
Uzasadnij, że oba kąty przy podstawie 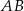 trójkąta
trójkąta 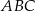 są równe.
są równe.
Dany jest trójkąt 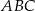 . Punkt
. Punkt 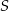 jest środkiem boku
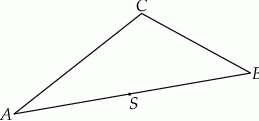
jest środkiem boku 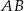 tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 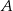 i
i 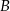 od prostej
od prostej 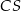 są równe.
są równe.
Na boku 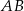 trójkąta
trójkąta 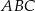 wybrano punkt
wybrano punkt 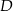 w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 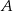 i
i 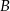 od prostej
od prostej 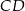 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 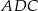 i
i 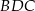 mają równe pola.
mają równe pola.
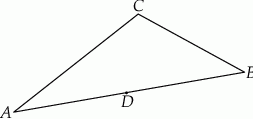
Na środkowej 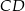 trójkąta
trójkąta 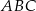 wybrano punkt
wybrano punkt 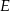 . Wykaż, że trójkąty
. Wykaż, że trójkąty 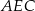 i
i 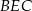 mają równe pola.
mają równe pola.
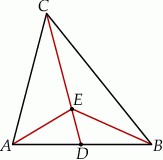
Wierzchołek 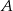 trójkąta ostrokątnego
trójkąta ostrokątnego 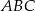 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 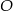 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 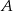 poprowadzono wysokość
poprowadzono wysokość 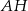 . Wykaż, że
. Wykaż, że 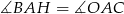 .
.
W trójkącie 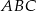 przedłużono bok
przedłużono bok 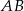 poza wierzchołek
poza wierzchołek 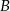 i odłożono odcinek
i odłożono odcinek 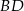 taki, że
taki, że 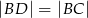 . Następnie połączono punkty
. Następnie połączono punkty 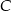 i
i 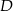 (rysunek). Wykaż, że
(rysunek). Wykaż, że 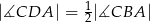 .
.
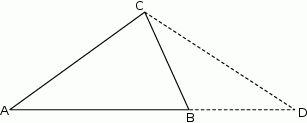
W trójkącie 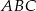 przedłużono bok
przedłużono bok 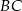 poza wierzchołek
poza wierzchołek 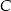 i odłożono odcinek
i odłożono odcinek 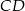 taki, że
taki, że 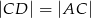 . Następnie połączono punkty
. Następnie połączono punkty 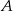 i
i 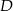 (rysunek). Wykaż, że
(rysunek). Wykaż, że 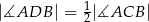 .
.
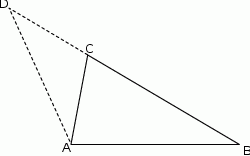
Na dwusiecznej 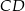 trójkąta
trójkąta 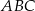 , w którym
, w którym 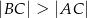 wybrano punkt
wybrano punkt 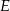 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 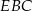 jest większe od pola trójkąta
jest większe od pola trójkąta 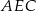 .
.
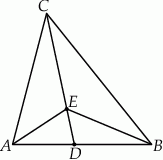
Wykaż, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i ma długość równą połowie tego boku.
Na boku 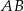 trójkąta
trójkąta 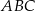 znajduje się taki punkt
znajduje się taki punkt 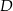 , że
, że 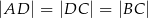 . Miara kąta
. Miara kąta 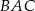 jest równa
jest równa 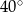 .
.
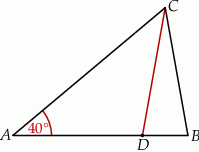
Uzasadnij, że miara kąta 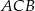 jest trzy większa od miary kąta
jest trzy większa od miary kąta 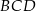 .
.
Na boku 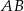 trójkąta
trójkąta 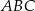 wybrano punkt
wybrano punkt 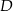 , a na odcinku
, a na odcinku 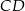 wybrano punkt
wybrano punkt 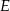 . Wykaż, że stosunek pól trójkątów
. Wykaż, że stosunek pól trójkątów 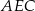 i
i 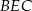 jest równy stosunkowi pól trójkątów
jest równy stosunkowi pól trójkątów 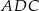 i
i 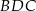 .
.
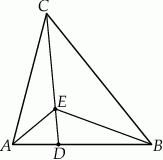
Środkowa  trójkąta
trójkąta  ma długość równą połowie długości boku
ma długość równą połowie długości boku  oraz
oraz 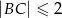 . Wykaż, że
. Wykaż, że 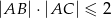 .
.
W trójkącie 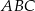 dwusieczna kąta przy wierzchołku
dwusieczna kąta przy wierzchołku 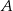 przecina symetralną boku
przecina symetralną boku 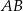 pod kątem
pod kątem 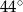 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 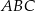 jest trójkątem rozwartokątnym.
jest trójkątem rozwartokątnym.
Punkty 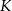 i
i 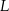 są środkami boków
są środkami boków 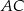 i
i 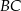 trójkąta
trójkąta 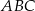 . Odcinki
. Odcinki 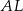 i
i 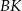 przecinają się w punkcie
przecinają się w punkcie 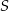 .
.
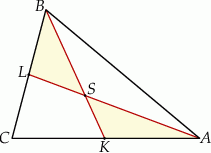
Uzasadnij, że pola trójkątów 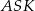 i
i 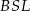 są równe.
są równe.
Punkty 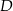 i
i 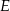 są środkami boków
są środkami boków 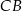 i
i 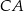 trójkąta
trójkąta 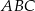 (zobacz rysunek). Wykaż, że odległość punktu
(zobacz rysunek). Wykaż, że odległość punktu 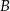 od prostej
od prostej 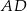 jest dwa razy większa od odległości punktu
jest dwa razy większa od odległości punktu 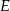 od prostej
od prostej 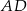 .
.
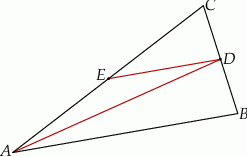
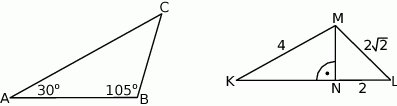
Uzasadnij, że trójkąty 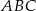 i
i 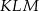 przedstawione na rysunku są podobne.
przedstawione na rysunku są podobne.