Uzasadnij, że nierówność 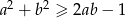 jest prawdziwa dla dowolnych liczb rzeczywistych
jest prawdziwa dla dowolnych liczb rzeczywistych  i
i 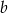 .
.
/Szkoła średnia/Nierówności/Udowodnij.../Kwadratowe
Ukryj
Podobne zadania
Wykaż, że dla każdej liczby rzeczywistej  różnej od 0 i każdej liczby rzeczywistej
różnej od 0 i każdej liczby rzeczywistej 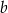 różnej od 0 spełniona jest nierówność
różnej od 0 spełniona jest nierówność
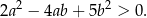
Wykaż, że dla każdych dwóch różnych liczb rzeczywistych  i
i 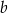 prawdziwa jest nierówność
prawdziwa jest nierówność
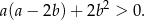
Wykaż, że dla każdych dwóch liczb rzeczywistych  i
i 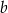 prawdziwa jest nierówność
prawdziwa jest nierówność
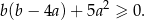
Udowodnij, że jeśli 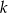 i
i  są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 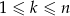 , to
, to 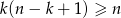 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 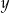 prawdziwa jest nierówność
prawdziwa jest nierówność
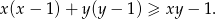
Ukryj
Podobne zadania
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 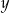 prawdziwa jest nierówność
prawdziwa jest nierówność
Udowodnij, że jeśli
 są liczbami rzeczywistymi, to
są liczbami rzeczywistymi, to 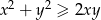 .
. 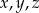 są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 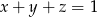 , to
, to 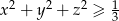 .
.

