Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 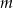 prawdziwa jest nierówność
prawdziwa jest nierówność 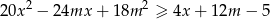 .
.
/Szkoła średnia/Nierówności/Udowodnij.../Kwadratowe
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 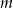 prawdziwa jest nierówność
prawdziwa jest nierówność 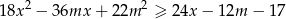 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 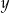 prawdziwa jest nierówność
prawdziwa jest nierówność 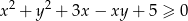 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 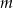 prawdziwa jest nierówność
prawdziwa jest nierówność 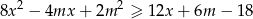 .
.
Wykaż, że dla każdej liczby rzeczywistej dodatniej  i dla każdej liczby rzeczywistej dodatniej
i dla każdej liczby rzeczywistej dodatniej 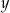 takiej, że
takiej, że 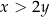 , prawdziwa jest nierówność
, prawdziwa jest nierówność
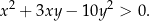
Wykaż, że dla każdych liczb rzeczywistych  oraz
oraz  prawdziwa jest nierówność
prawdziwa jest nierówność
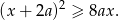
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 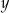 takich, że
takich, że 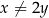 , prawdziwa jest nierówność
, prawdziwa jest nierówność
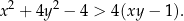
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 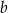 spełniona jest nierówność
spełniona jest nierówność
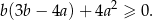
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 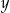 takich, że
takich, że 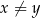 prawdziwa jest nierówność
prawdziwa jest nierówność
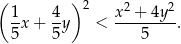
Wykaż, że dla dowolnych różnych liczb rzeczywistych  i
i 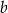 prawdziwa jest nierówność
prawdziwa jest nierówność
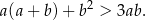
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 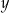 takich, że
takich, że 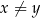 , prawdziwa jest nierówność
, prawdziwa jest nierówność
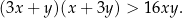
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 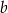 prawdziwa jest nierówność
prawdziwa jest nierówność
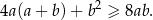
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 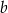 spełniona jest nierówność
spełniona jest nierówność
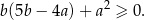
Wykaż, że dla dowolnej liczby całkowitej 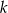 prawdziwa jest nierówność
prawdziwa jest nierówność 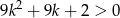 .
.
Wykaż, że dla dowolnej liczby całkowitej 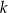 prawdziwa jest nierówność
prawdziwa jest nierówność 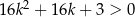 .
.
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 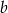 prawdziwa jest nierówność
prawdziwa jest nierówność
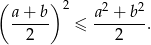
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 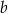 takich, że
takich, że 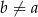 , spełniona jest nierówność
, spełniona jest nierówność
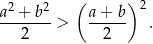
Wykaż, ze dla dowolnych liczb rzeczywistych 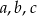 prawdziwa jest nierówność
prawdziwa jest nierówność
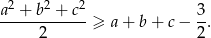
Wykaż, że dla 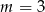 nierówność
nierówność 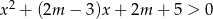 jest spełniona przez wszystkie liczby rzeczywiste
jest spełniona przez wszystkie liczby rzeczywiste  .
.
Wykaż, że rozwiązaniem nierówności 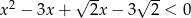 jest przedział
jest przedział 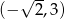 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 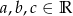 zachodzi nierówność
zachodzi nierówność
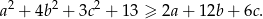
Udowodnij, że dla dowolnych liczb rzeczywistych 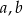 prawdziwa jest nierówność
prawdziwa jest nierówność
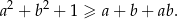
Wykaż, że jeżeli 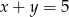 , to
, to 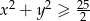 .
.
Wykaż, że jeżeli 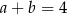 , to
, to 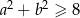 .
.
Wykaż, że jeżeli 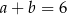 , to
, to 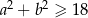 .
.
Wykaż, że dla każdej liczby rzeczywistej  większej od 2 i dla każdej liczby rzeczywistej
większej od 2 i dla każdej liczby rzeczywistej 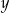 prawdziwa jest nierówność
prawdziwa jest nierówność 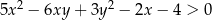 .
.
Wykaż, że dla każdej liczby rzeczywistej  mniejszej od
mniejszej od 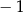 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 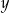 prawdziwa jest nierówność
prawdziwa jest nierówność 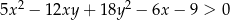 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 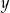 większej od 1 prawdziwa jest nierówność
większej od 1 prawdziwa jest nierówność 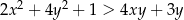 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 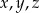 takich, że
takich, że 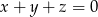 , prawdziwa jest nierówność
, prawdziwa jest nierówność 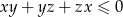 .
.
Możesz skorzystać z tożsamości 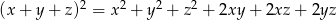 .
.
Udowodnij, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 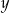 prawdziwa jest nierówność
prawdziwa jest nierówność
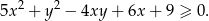
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 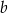 prawdziwa jest nierówność
prawdziwa jest nierówność
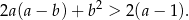
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 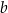 takiej, że
takiej, że 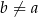 , prawdziwa jest nierówność
, prawdziwa jest nierówność
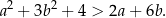
Wykaż, ze dla dowolnych liczb rzeczywistych 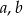 prawdziwa jest nierówność
prawdziwa jest nierówność 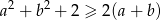 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 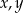 prawdziwa jest nierówność
prawdziwa jest nierówność 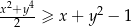 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 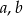 prawdziwa jest nierówność
prawdziwa jest nierówność 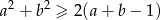 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 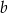 prawdziwa jest nierówność
prawdziwa jest nierówność
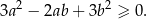
Wykaż, ze dla dowolnych liczb rzeczywistych 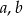 prawdziwa jest nierówność
prawdziwa jest nierówność 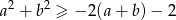 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 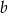 prawdziwa jest nierówność
prawdziwa jest nierówność
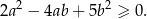
Wykaż, ze dla dowolnych liczb rzeczywistych 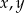 prawdziwa jest nierówność
prawdziwa jest nierówność 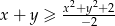 .
.
Wykaż, że dla każdej liczby rzeczywistej 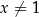 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 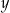 prawdziwa jest nierówność
prawdziwa jest nierówność
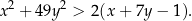
Wykaż, ze dla dowolnych liczb rzeczywistych 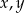 prawdziwa jest nierówność
prawdziwa jest nierówność 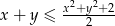 .
.
Wykaż, że dla każdej liczby rzeczywistej 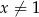 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 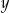 prawdziwa jest nierówność
prawdziwa jest nierówność
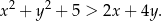
Wykaż, ze dla dowolnych liczb rzeczywistych 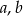 prawdziwa jest nierówność
prawdziwa jest nierówność 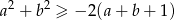 .
.
Wykaż, że jeżeli 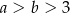 , to
, to 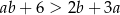 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 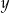 prawdziwa jest nierówność
prawdziwa jest nierówność 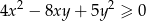 .
.
Udowodnij, że dla dowolnych liczb rzeczywistych 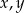 prawdziwa jest nierówność
prawdziwa jest nierówność 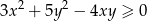 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 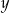 prawdziwa jest nierówność
prawdziwa jest nierówność 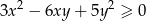 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 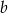 prawdziwa jest nierówność
prawdziwa jest nierówność 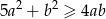 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 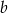 prawdziwa jest nierówność
prawdziwa jest nierówność 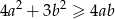 .
.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność 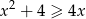 .
.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność 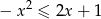 .
.
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność 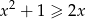 .
.
Uzasadnij, że jeżeli liczby rzeczywiste 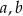 spełniają warunek
spełniają warunek 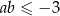 , to
, to 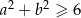 .
.
Dana jest nierówność kwadratowa z parametrem 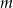 :
:
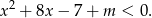
- Wyznacz wszystkie wartości parametru
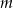 , dla których przedział
, dla których przedział 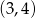 zawiera się w zbiorze rozwiązań tej nierówności.
zawiera się w zbiorze rozwiązań tej nierówności. - Uzasadnij, że jeżeli dla pewnej wartości parametru
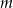 nierówność ta ma rozwiązanie w przedziale
nierówność ta ma rozwiązanie w przedziale 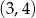 , to ma ona w tym przedziale nieskończenie wiele rozwiązań.
, to ma ona w tym przedziale nieskończenie wiele rozwiązań.

