Dany jest okrąg 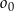 o równaniu
o równaniu 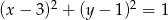 . W pierwszej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W pierwszej „ćwiartce” układu współrzędnych istnieją dwa okręgi 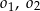 styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 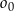 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 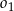 oraz
oraz 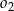 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Wzajemnie styczne
Dany jest okrąg 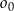 o równaniu
o równaniu 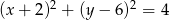 . W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi 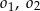 styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 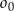 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 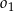 oraz
oraz 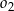 .
.
Dane są dwa okręgi o równaniach 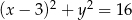 i
i 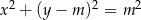 ,
, 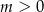 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 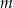 , dla których te okręgi mają jeden punkt wspólny.
, dla których te okręgi mają jeden punkt wspólny.
Dane są dwa okręgi o równaniach 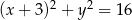 i
i 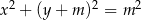 ,
, 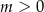 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 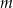 , dla których te okręgi mają jeden punkt wspólny.
, dla których te okręgi mają jeden punkt wspólny.
Dany jest okrąg o środku w punkcie 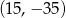 i promieniu 16. Sprawdź czy okrąg ten jest styczny do
i promieniu 16. Sprawdź czy okrąg ten jest styczny do
- prostej
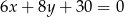 ,
, - okręgu o środku w punkcie
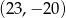 i promieniu 2?
i promieniu 2?
Uzasadnij swoją odpowiedź.
Okrąg o środku w punkcie 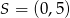 ma promień długości 1 i jest styczny do okręgu o środku
ma promień długości 1 i jest styczny do okręgu o środku 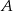 i promieniu długości 10. Punkt
i promieniu długości 10. Punkt 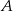 leży na osi
leży na osi 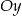 . Jakie ma współrzędne?
. Jakie ma współrzędne?
Wyznacz równanie okręgu stycznego wewnętrznie do okręgu o równaniu 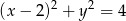 i do prostej
i do prostej 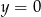 , którego środek ma współrzędne różnych znaków i leży na wykresie funkcji
, którego środek ma współrzędne różnych znaków i leży na wykresie funkcji 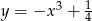 .
.
Dane są okręgi o równaniach 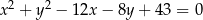 i
i 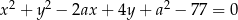 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
Dane są okręgi o równaniach 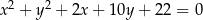 i
i 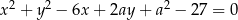 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru  , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.
, dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.

