Stożek/Stereometria/Geometria - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Stożek

Kąt rozwarcia stożka jest równy 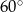∘ 60 . Promień podstawy stożka ma długość 4. Oblicz pole powierzchni bocznej stożka.

Stosunek pola powierzchni bocznej stożka do pola jego powierzchni całkowitej jest równy . Wyznacz miarę kąta nachylenia tworzącej stożka do płaszczyzny podstawy.

Podstawa stożka o kącie rozwarcia 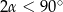∘ 2α < 90 jest kołem wielkim kuli. Oblicz objętość tego stożka jeżeli jego powierzchnia boczna wycina z powierzchni kuli okrąg o promieniu .

W stożek o promieniu podstawy długości 6 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz promień podstawy walca, jeżeli jego objętość stanowi 4 9 objętości stożka.

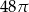Tworząca stożka o kącie rozwarcia ma długość 8. Pole powierzchni całkowitej tego stożka jest równe 48π . Oblicz objętość stożka oraz miarę kąta .

Ukryj Podobne zadania

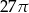Tworząca stożka o kącie rozwarcia ma długość 6. Pole powierzchni całkowitej tego stożka jest równe 27π . Oblicz objętość stożka oraz miarę kąta .

Tworząca stożka jest nachylona do podstawy pod kątem . Kula opisana na tym stożku ma promień 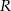. Oblicz pole powierzchni całkowitej tego stożka.

Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka

Ukryj Podobne zadania

Pole powierzchni bocznej stożka jest trzy razy większe od pola jego podstawy. Wysokość tego stożka jest równa 12. Oblicz objętość tego stożka.

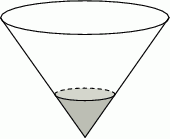
Do pojemnika w kształcie stożka wlano 1 litr wody, która wypełniła to naczynie do 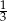wysokości. Jaka jest całkowita pojemność tego naczynia?

Dany jest stożek o polu powierzchni bocznej równym 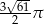3√-61 2 π , w którym tangens kąta nachylenia tworzącej do podstawy jest równy . Oblicz objętość tego stożka.

Odległość środka wysokości stożka od jego powierzchni bocznej jest trzy razy mniejsza niż promień jego podstawy. Oblicz sinus kąta rozwarcia stożka.

Tomek i Marek chcą wejść docelowo na szczyt pewnej góry. W chwili początkowej znajdują się w punkcie położonym na stoku góry dokładnie na północ od szczytu na wysokości metrów n.p.m. Tomek i Marek chcą dotrzeć do bazy znajdującej się dokładnie na południe od szczytu na przeciwległym południowym stoku góry na wysokości H 1 metrów n.p.m., a następnie z bazy wejść na szczyt leżący na wysokości H 2 metrów n.p.m. (zobacz rysunek).

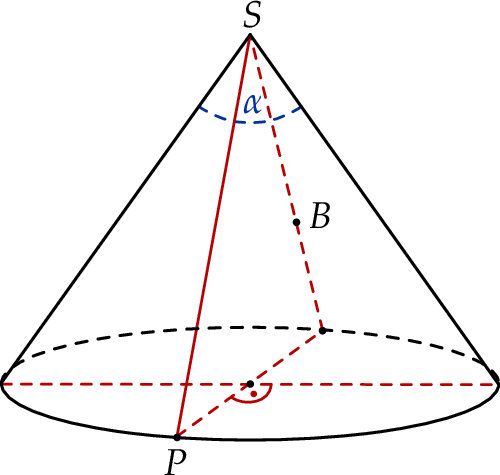
ZINFO-FIGURE

Oblicz długość najkrótszej drogi, jaką muszą pokonać, aby dotrzeć do bazy. Przyjmij, że góra jest stożkiem o kącie rozwarcia .

Oblicz objętość stożka, którego tworząca o długości 4 jest nachylona do płaszczyzny podstawy pod kątem 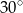30 ∘ .

Czy kwadratową płytą o boku długości 2,2 m można całkowicie zakryć otwór w ziemi, który ma kształt stożka o wysokości 2 m i kącie rozwarcia 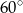60∘ ?

Odpowiedź uzasadnij.

Do naczynia w kształcie odwróconego stożka wrzucono kulkę o promieniu 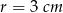r = 3 cm . Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.

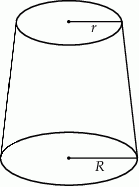
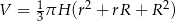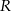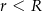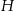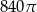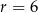Objętość stożka ściętego (przedstawionego na rysunku) można obliczyć ze wzoru V = 13πH (r2 + rR + R 2) , gdzie i są promieniami podstaw ( r < R ), a jest wysokością bryły. Dany jest stożek ścięty, którego wysokość jest równa 10, objętość 840π , a r = 6 . Oblicz cosinus kąta nachylenia przekątnej przekroju osiowego tej bryły do jednej z jej podstaw.

Strona 3 z 3