Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest półkolem. Oblicz miarę kąta rozwarcia stożka.
/Szkoła średnia/Geometria/Stereometria/Stożek
Przekrój osiowy stożka jest trójkątem równobocznym o polu 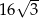 . Oblicz objętość i pole powierzchni całkowitej tego stożka.
. Oblicz objętość i pole powierzchni całkowitej tego stożka.
Pole powierzchni bocznej stożka jest czterokrotnie większe od pola podstawy stożka. Oblicz wysokość stożka, wiedząc, że promień jego podstawy jest równy  .
.
Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy 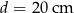 , wysokości
, wysokości 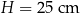 i tworzącej
i tworzącej 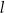 . Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską
. Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską 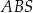 o kształcie wycinka koła o promieniu
o kształcie wycinka koła o promieniu 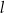 i środku
i środku 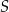 . Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek
. Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek 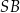 z odcinkiem
z odcinkiem 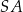 .
.

Oblicz miarę kąta 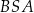 wycinka koła, z którego powstała powierzchnia boczna stożka. Miarę kąta
wycinka koła, z którego powstała powierzchnia boczna stożka. Miarę kąta 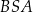 podaj w zaokrągleniu do jednego stopnia.
podaj w zaokrągleniu do jednego stopnia.
Metalowy walec o objętości 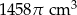 i przekroju będącym kwadratem przetopiono na stożek o takim samym promieniu podstawy, co walec. Oblicz stosunek pola powierzchni bocznej otrzymanego stożka do pola powierzchni bocznej wyjściowego walca.
i przekroju będącym kwadratem przetopiono na stożek o takim samym promieniu podstawy, co walec. Oblicz stosunek pola powierzchni bocznej otrzymanego stożka do pola powierzchni bocznej wyjściowego walca.
W stożku o promieniu podstawy  tworząca jest nachylona do płaszczyzny podstawy pod kątem
tworząca jest nachylona do płaszczyzny podstawy pod kątem  . Przez wierzchołek stożka poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod kątem
. Przez wierzchołek stożka poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod kątem 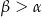 .
.
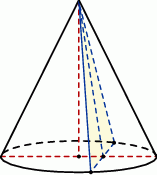
Wykaż, że pole otrzymanego przekroju stożka jest równe
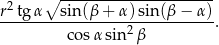
Pole powierzchni całkowitej stożka jest trzy razy większe od pola jego podstawy. Oblicz miarę kąta rozwarcia tego stożka.
Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym, o polu równym 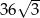 . Płaszczyzna
. Płaszczyzna  , do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej
, do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej 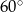 . Oblicz objętość stożka.
. Oblicz objętość stożka.
Cosinus kąta rozwarcia stożka jest równy 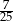 . Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
. Odległość środka kuli wpisanej w ten stożek od jego wierzchołka jest równa 10. Oblicz pole powierzchni bocznej stożka.
Rozwinięcie powierzchni bocznej stożka jest wycinkiem kołowym o kącie środkowym  . Kąt ten oparty jest na łuku długości
. Kąt ten oparty jest na łuku długości  . Oblicz objętość stożka.
. Oblicz objętość stożka.
W kulę o promieniu 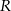 wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem
wpisano stożek. Ze środka tej kuli widać tworzącą stożka pod kątem  . Oblicz objętość stożka.
. Oblicz objętość stożka.
Powierzchnia boczna stożka jest wycinkiem kołowym, którego kąt środkowy ma miarę 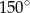 . Wiedząc, że tworząca stożka ma długość 24 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
. Wiedząc, że tworząca stożka ma długość 24 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
Powierzchnia boczna stożka jest wycinkiem kołowym, którego kąt środkowy ma miarę 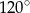 . Wiedząc, że tworząca stożka ma długość 12 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
. Wiedząc, że tworząca stożka ma długość 12 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
Wysokość walca wpisanego w stożek jest równa promieniowi podstawy stożka. Stosunek objętości stożka do objętości walca wynosi 8 : 3. Oblicz tangens kąta zawartego między wysokością a tworzącą stożka.
Tworząca stożka jest nachylona do podstawy pod kątem  . Kula opisana na tym stożku ma promień
. Kula opisana na tym stożku ma promień 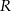 . Oblicz objętość tego stożka.
. Oblicz objętość tego stożka.
Pole powierzchni całkowitej 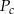 stożka oraz jego pole podstawy
stożka oraz jego pole podstawy 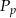 spełniają równanie
spełniają równanie 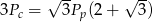 . Oblicz miarę kąta rozwarcia stożka.
. Oblicz miarę kąta rozwarcia stożka.
Metalową kulę o promieniu 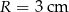 przetopiono na stożek. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem
przetopiono na stożek. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem  , takim, że
, takim, że 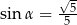 . Wyznacz promień podstawy tego stożka.
. Wyznacz promień podstawy tego stożka.
Stożek ma wysokość 10 cm. Pole przekroju osiowego tego stożka jest równe 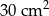 . Jaką długość ma tworząca tego stożka?
. Jaką długość ma tworząca tego stożka?
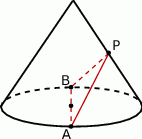
Środek 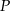 tworzącej stożka połączono z końcami
tworzącej stożka połączono z końcami 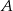 i
i 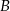 średnicy koła w podstawie stożka tak, że
średnicy koła w podstawie stożka tak, że 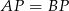 . Wiedząc, że kąt rozwarcia stożka jest równy
. Wiedząc, że kąt rozwarcia stożka jest równy 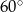 , oblicz kąty trójkąta
, oblicz kąty trójkąta 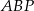 .
.
Powierzchnia boczna stożka jest po rozwinięciu ćwiartką koła o promieniu 16 cm. Oblicz pole powierzchni całkowitej i objętość tego stożka.
Powierzchnia boczna stożka jest po rozwinięciu ćwiartką koła o promieniu 12 cm. Oblicz pole powierzchni całkowitej i objętość tego stożka.
Stosunek pola powierzchni bocznej stożka do pola przekroju osiowego tego stożka jest równy 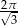 . Oblicz kąt rozwarcia stożka.
. Oblicz kąt rozwarcia stożka.
Stosunek pola powierzchni bocznej stożka do pola przekroju osiowego tego stożka jest równy 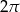 . Oblicz kąt rozwarcia stożka.
. Oblicz kąt rozwarcia stożka.

