Funkcja homograficzna jest określona wzorem 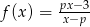 gdzie
gdzie 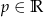 i
i 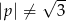 .
.
- Dla
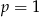 zapisz wzór funkcji w postaci
zapisz wzór funkcji w postaci 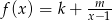 , gdzie
, gdzie 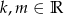 .
. - Wyznacz wszystkie wartosci
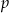 , dla których w przedziale
, dla których w przedziale 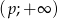 funkcja jest malejąca.
funkcja jest malejąca.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Funkcja homograficzna jest określona wzorem 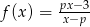 gdzie
gdzie 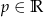 i
i 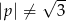 .
.
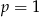 zapisz wzór funkcji w postaci
zapisz wzór funkcji w postaci 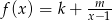 , gdzie
, gdzie 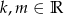 .
. 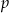 , dla których w przedziale
, dla których w przedziale 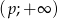 funkcja jest malejąca.
funkcja jest malejąca.Funkcja 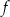 jest określona wzorem
jest określona wzorem 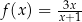 dla każdego
dla każdego 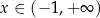 . Wykaż, że
. Wykaż, że 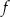 jest funkcją rosnącą.
jest funkcją rosnącą.
Funkcja homograficzna 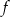 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 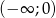 i
i 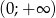 . Zbiór
. Zbiór 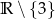 jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
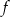 .
. 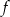 .
. 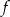 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.Wyznacz wszystkie wartości parametru 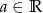 , dla których funkcja
, dla których funkcja 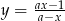 jest rosnąca w każdym przedziale, na którym jest określona. Dla
jest rosnąca w każdym przedziale, na którym jest określona. Dla 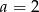 wyznacz zbiór wartości funkcji.
wyznacz zbiór wartości funkcji.
Funkcja 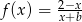 przyjmuje wartości ujemne wtedy i tylko wtedy gdy
przyjmuje wartości ujemne wtedy i tylko wtedy gdy 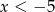 lub
lub 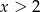 .
.
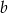 .
. 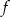 w postaci kanonicznej.
w postaci kanonicznej. 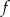 osiąga wartości nie większe niż funkcja
osiąga wartości nie większe niż funkcja 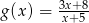 .
.Funkcja homograficzna 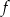 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 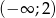 i
i 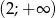 . Zbiór
. Zbiór 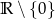 jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
jest zbiorem wartości tej funkcji, a wartość 1 funkcja przyjmuje dla argumentu 6.
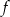 .
. 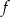 .
. 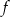 nie jest monotoniczna w zbiorze
nie jest monotoniczna w zbiorze 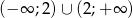 .
.Funkcja 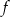 jest określona wzorem
jest określona wzorem 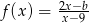 dla
dla 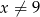 . Ponadto wiemy, że
. Ponadto wiemy, że 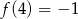 . Oblicz współczynnik
. Oblicz współczynnik 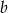 .
.
W prostokątnym układzie współrzędnych zaznacz zbiór tych wszystkich punktów płaszczyzny o współrzędnych 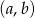 , dla których funkcja
, dla których funkcja 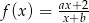 jest funkcją homograficzną, malejącą w każdym z przedziałów:
jest funkcją homograficzną, malejącą w każdym z przedziałów: 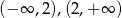 .
.
