Dla jakich wartości parametru  suma kwadratów różnych pierwiastków równania
suma kwadratów różnych pierwiastków równania
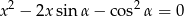
jest równa 3?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla jakich wartości parametru  suma kwadratów różnych pierwiastków równania
suma kwadratów różnych pierwiastków równania
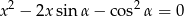
jest równa 3?
Dla jakiego 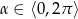 pierwiastki równania
pierwiastki równania
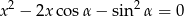
spełniają warunek 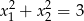 ?
?
Wyznacz wszystkie wartości parametru 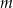 , dla których równanie
, dla których równanie
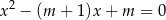
ma dwa różne rozwiązania rzeczywiste 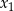 oraz
oraz 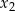 , spełniające warunki:
, spełniające warunki:
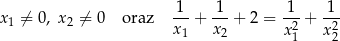
Zbadaj liczbę rozwiązań równania ze względu na wartość parametru 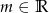 . Napisz wzór i narysuj wykres funkcji
. Napisz wzór i narysuj wykres funkcji 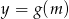 , która każdej wartości parametru
, która każdej wartości parametru 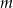 przyporządkowuje liczbę rozwiązań równania
przyporządkowuje liczbę rozwiązań równania 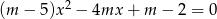 .
.
Wyznacz wszystkie wartości parametru 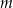 , dla których równanie
, dla których równanie
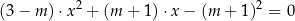
ma dwa różne rozwiązania rzeczywiste 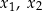 spełniające warunek
spełniające warunek
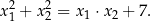
Liczby 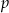 i
i 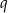 są pierwiastkami równania
są pierwiastkami równania 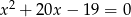 . Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia
. Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia 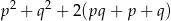 .
.
Liczby 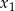 i
i 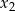 są pierwiastkami równania
są pierwiastkami równania 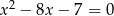 . Oblicz
. Oblicz 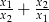 .
.
Liczby 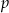 i
i 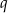 są pierwiastkami równania
są pierwiastkami równania 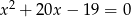 . Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia
. Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia 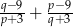 .
.
Liczby 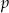 i
i 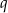 są pierwiastkami równania
są pierwiastkami równania 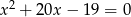 . Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia
. Nie obliczając pierwiastków tego równania, oblicz wartość wyrażenia 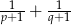 .
.
Liczby 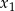 i
i 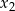 są pierwiastkami równania
są pierwiastkami równania 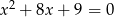 . Oblicz
. Oblicz 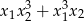 .
.
Liczby 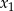 i
i 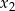 są pierwiastkami równania
są pierwiastkami równania 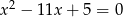 . Oblicz
. Oblicz 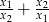 .
.
Dla jakich wartości parametru  równanie
równanie 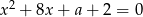 ma dwa różne pierwiastki jednakowych znaków?
ma dwa różne pierwiastki jednakowych znaków?
Dla jakich wartości parametru 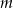 suma odwrotności pierwiastków równania
suma odwrotności pierwiastków równania 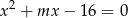 jest równa -4?
jest równa -4?
Wyznacz wszystkie wartości parametru 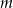 , dla których jeden z pierwiastków równania
, dla których jeden z pierwiastków równania
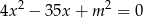
jest kwadratem drugiego pierwiastka. Oblicz te pierwiastki.
Wyznacz te wartości parametru  , dla których różne pierwiastki
, dla których różne pierwiastki 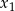 i
i 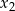 równania
równania 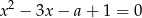 spełniają warunek
spełniają warunek 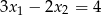 .
.
Rozwiąż równanie 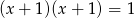 .
.
Rozwiąż równanie kwadratowe 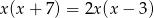 .
.
Rozwiąż równanie 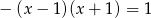 .
.
Rozwiąż równanie 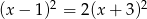 .
.
Rozwiąż równanie 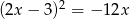 .
.
Rozwiąż równanie 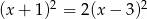 .
.
Dla jakich wartości parametru 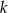 równanie
równanie 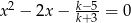 ma dwa pierwiastki jednakowych znaków, których suma kwadratów jest nie mniejsza od 3?
ma dwa pierwiastki jednakowych znaków, których suma kwadratów jest nie mniejsza od 3?
Suma pierwiastków trójmianu 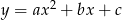 jest równa
jest równa 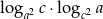 , gdzie
, gdzie 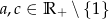 . Uzasadnij, że odcięta wierzchołka paraboli będącej wykresem tego trójmianu jest równa
. Uzasadnij, że odcięta wierzchołka paraboli będącej wykresem tego trójmianu jest równa  .
.
Dla jakich wartości parametru 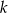 miejsca zerowe funkcji
miejsca zerowe funkcji 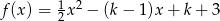 należą do przedziału
należą do przedziału 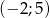 ?
?
Dla jakich wartości parametru 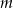 miejsca zerowe funkcji
miejsca zerowe funkcji 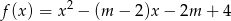 należą do przedziału
należą do przedziału 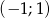 ?
?
Wyznacz wszystkie wartości parametru 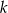 , dla których równanie
, dla których równanie 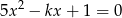 ma dwa różne pierwiastki, których różnica jest liczbą z przedziału
ma dwa różne pierwiastki, których różnica jest liczbą z przedziału 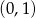 .
.
Wyznacz wszystkie wartości parametru 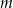 , dla których równanie
, dla których równanie 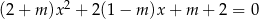 ma dwa różne pierwiastki rzeczywiste i kwadrat sumy odwrotności tych pierwiastków nie jest mniejszy od 0,5.
ma dwa różne pierwiastki rzeczywiste i kwadrat sumy odwrotności tych pierwiastków nie jest mniejszy od 0,5.
Pierwiastkami trójmianu kwadratowego 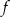 o współczynniku
o współczynniku 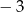 przy najwyższej potędze są liczby
przy najwyższej potędze są liczby 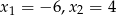 . Oblicz
. Oblicz 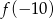 .
.
