Rozłóż na czynniki liniowe trójmian kwadratowy 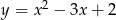 .
.
/Szkoła średnia/Równania/Kwadratowe
Rozłóż na czynniki wielomian 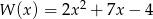 .
.
Wyznacz wszystkie wartości parametru 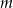 , dla których równanie
, dla których równanie 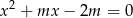 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 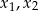 spełniające warunek
spełniające warunek 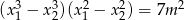 .
.
Oblicz sumę i iloczyn pierwiastków równania 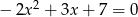 .
.
Dla jakich wartości parametru 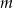 równanie
równanie 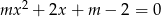 ma dwa różne pierwiastki mniejsze od 1?
ma dwa różne pierwiastki mniejsze od 1?
Jedno z miejsc zerowych trójmianu 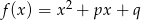 jest równe -1. Znajdź związek między
jest równe -1. Znajdź związek między 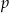 i
i 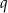 .
.
Funkcja kwadratowa postaci 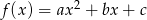 , posiada miejsca zerowe równe -3 i 2, a jej współczynnik
, posiada miejsca zerowe równe -3 i 2, a jej współczynnik 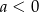 . Oblicz wartości współczynników
. Oblicz wartości współczynników 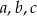 wiedząc, ze największa wartość funkcji wynosi
wiedząc, ze największa wartość funkcji wynosi 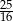 .
.
Określ liczbę pierwiastków równania 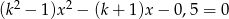 w zależności od wartości parametru
w zależności od wartości parametru 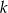 .
.
Wyznacz taki współczynnik 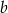 aby funkcja
aby funkcja 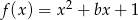 miała jedno miejsce zerowe.
miała jedno miejsce zerowe.
Wyznacz taki współczynnik 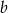 aby funkcja
aby funkcja 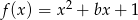 miała co najwyżej jedno miejsce zerowe.
miała co najwyżej jedno miejsce zerowe.
Wyznacz taki współczynnik 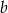 aby funkcja
aby funkcja 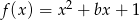 miała dwa miejsca zerowe.
miała dwa miejsca zerowe.
Określ liczbę pierwiastków równania 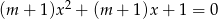 w zależności od wartości parametru
w zależności od wartości parametru 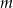 , a następnie naszkicuj wykres funkcji:
, a następnie naszkicuj wykres funkcji:

W prostokątnym układzie współrzędnych narysuj zbiór tych wszystkich punktów o współrzędnych 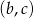 , dla których różne pierwiastki
, dla których różne pierwiastki 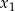 i
i 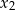 równania
równania 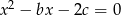 spełniają warunek
spełniają warunek 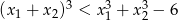 .
.
Nie obliczając pierwiastków równania 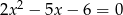 , oblicz
, oblicz
- ich iloczyn,
- sumę ich odwrotności
- ich sumę kwadratów.
Nie obliczając pierwiastków równania 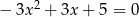 , oblicz
, oblicz
- ich sumę,
- sumę ich odwrotności
- kwadrat ich różnicy.
Dane jest równanie kwadratowe 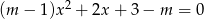 z niewiadomą
z niewiadomą  i parametrem
i parametrem 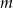 .
.
- Znajdź wzór i dziedzinę funkcji
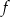 , która zmiennej rzeczywistej
, która zmiennej rzeczywistej 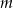 przyporządkowuje iloczyn dwóch różnych pierwiastków danego równania. Naszkicuj wykres funkcji
przyporządkowuje iloczyn dwóch różnych pierwiastków danego równania. Naszkicuj wykres funkcji 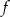 w prostokątnym układzie współrzędnych.
w prostokątnym układzie współrzędnych. - Wykaż, że do wykresu funkcji
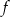 należą tylko trzy punkty o obu współrzędnych całkowitych.
należą tylko trzy punkty o obu współrzędnych całkowitych.
Dla jakich wartości parametru 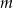 pierwiastkami równania
pierwiastkami równania 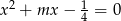 są liczby liczby
są liczby liczby 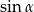 i
i 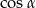 dla pewnego
dla pewnego 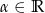 ?
?
Rozwiąż równanie 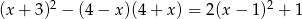 .
.
Rozwiąż równanie 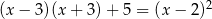 .
.
Rozwiąż równanie 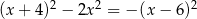 .
.
Rozwiąż równanie 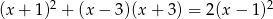 .
.
Rozwiąż równanie 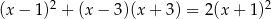 .
.
Rozwiąż równanie 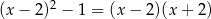 .
.
Rozwiąż równanie 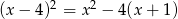 .
.
Rozwiąż równanie 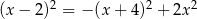 .
.
Rozwiąż równanie 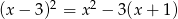 .
.
Rozwiąż równanie 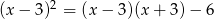 .
.
Rozwiąż równanie 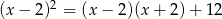 .
.
Dla jakich wartości parametru 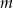 funkcja
funkcja 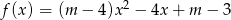 ma dwa miejsca zerowe, z których jedno jest mniejsze od 1, a drugie większe od 1?
ma dwa miejsca zerowe, z których jedno jest mniejsze od 1, a drugie większe od 1?
Wyznacz te wartości parametru 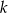 , dla których równanie
, dla których równanie 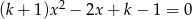 ma dwa różne rozwiązania należące do przedziału
ma dwa różne rozwiązania należące do przedziału 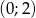 .
.
Naszkicuj wykres funkcji, która każdej liczbie rzeczywistej 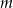 przyporządkowuje liczbę pierwiastków równania
przyporządkowuje liczbę pierwiastków równania
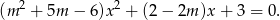
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 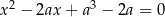 dwa różne rozwiązania dodatnie.
dwa różne rozwiązania dodatnie.
Wyznacz wszystkie wartości parametru 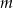 , dla których prosta o równaniu
, dla których prosta o równaniu 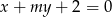 ma dokładnie dwa punkty wspólne z parabolą o równaniu
ma dokładnie dwa punkty wspólne z parabolą o równaniu 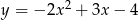 .
.
Dla jakich wartości parametru 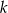 równanie
równanie 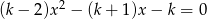 ma tylko ujemne rozwiązania?
ma tylko ujemne rozwiązania?
Dla jakich wartości 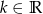 równanie
równanie 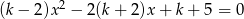 ma dwa różne pierwiastki dodatnie?
ma dwa różne pierwiastki dodatnie?
Wyznacz wszystkie wartości parametru 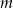 , dla których równanie
, dla których równanie 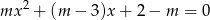 ma dwa rozwiązania dodatnie.
ma dwa rozwiązania dodatnie.
Dla jakich wartości 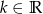 równanie
równanie 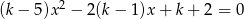 ma dwa różne pierwiastki dodatnie?
ma dwa różne pierwiastki dodatnie?

