Dla jakich wartości parametru 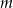 równanie
równanie 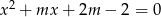 ma dwa pierwiastki, z których jeden jest sinusem, a drugi cosinusem tego samego kąta?
ma dwa pierwiastki, z których jeden jest sinusem, a drugi cosinusem tego samego kąta?
/Szkoła średnia/Równania/Kwadratowe
Wyznacz wszystkie wartości parametru 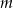 , dla których jedno rozwiązanie równania
, dla których jedno rozwiązanie równania
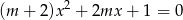
jest sinusem, a drugie cosinusem tego samego kąta?
Podaj wzór i naszkicuj wykres funkcji przyporządkowującej każdej wartości parametru 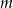 , dla której istnieją dwa różne pierwiastki równania
, dla której istnieją dwa różne pierwiastki równania 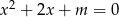 , iloczyn pierwiastków tego równania.
, iloczyn pierwiastków tego równania.
Znajdź takie wartości parametru 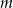 , aby połowa jednego pierwiastka równania
, aby połowa jednego pierwiastka równania 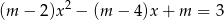 była równa odwrotności drugiego pierwiastka.
była równa odwrotności drugiego pierwiastka.
Wyznacz te wartości parametru 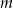 , dla których równanie
, dla których równanie
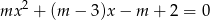
ma co najmniej jedno dodatnie rozwiązanie.
Wyznacz wszystkie wartości parametru 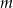 , dla których równanie
, dla których równanie
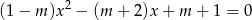
ma przynajmniej jedno rozwiązanie ujemne.
Wykaż, że jeśli funkcja kwadratowa 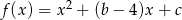 osiąga najmniejszą wartość dla argumentu
osiąga najmniejszą wartość dla argumentu  , to ma dwa rózne miejsca zerowe wtedy i tylko wtedy, gdy
, to ma dwa rózne miejsca zerowe wtedy i tylko wtedy, gdy 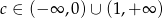 .
.
Znajdź tę wartość parametru 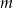 , dla której iloczyn pierwiastków równania
, dla której iloczyn pierwiastków równania 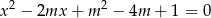 jest najmniejszy.
jest najmniejszy.
Dana jest funkcja kwadratowa 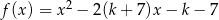 określona dla dowolnego
określona dla dowolnego 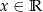 . Wykaż, że jeżeli funkcja
. Wykaż, że jeżeli funkcja 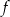 ma dwa różne miejsca zerowe:
ma dwa różne miejsca zerowe: 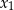 i
i 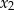 , to miejscami zerowymi funkcji
, to miejscami zerowymi funkcji 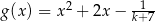 , określonej dla
, określonej dla 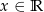 , są liczby
, są liczby 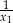 i
i 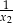 .
.
Wyznacz wszystkie wartości parametru 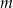 , dla których równanie
, dla których równanie
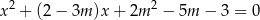
ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 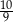 .
.
Dla jakich wartości parametru 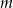 równanie
równanie 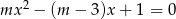 ma różne pierwiastki
ma różne pierwiastki 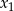 i
i 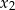 spełniające warunek
spełniające warunek 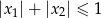 ?
?
Dla jakich wartości parametru 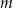 równanie
równanie 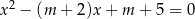 ma dwa pierwiastki różnych znaków
ma dwa pierwiastki różnych znaków 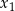 i
i 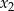 spełniające warunek
spełniające warunek 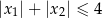 ?
?
Bez wyznaczania pierwiastków równania 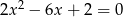 , określ ich znak.
, określ ich znak.
Liczba 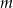 jest sumą odwrotności dwóch różnych pierwiastków równania
jest sumą odwrotności dwóch różnych pierwiastków równania
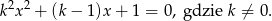
Wyznacz zbiór wartości funkcji określonej wzorem 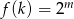 .
.
Liczba 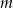 jest sumą odwrotności dwóch różnych pierwiastków równania
jest sumą odwrotności dwóch różnych pierwiastków równania
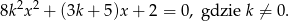
Wyznacz zbiór wartości funkcji określonej wzorem 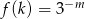 .
.
Wyznacz wszystkie wartości parametru 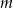 , dla których równanie
, dla których równanie 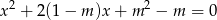 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 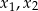 spełniające warunek
spełniające warunek 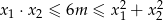 .
.
Wyznacz wszystkie wartości parametru 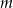 , dla których równanie
, dla których równanie 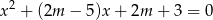 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 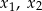 takie, że
takie, że 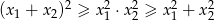 .
.
Wyznacz wszystkie wartości parametru 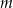 , dla których równanie
, dla których równanie
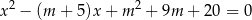
ma dwa różne rozwiązania rzeczywiste 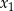 oraz
oraz 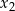 , spełniające warunek
, spełniające warunek
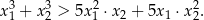
Wyznacz wszystkie wartości parametru 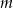 , dla których równanie
, dla których równanie 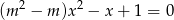 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 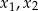 takie, że
takie, że 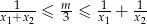 .
.
Wyznacz wszystkie wartości parametru 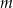 , dla których równanie
, dla których równanie 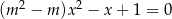 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 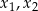 takie, że
takie, że 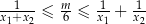 .
.
Wyznacz wszystkie wartości parametru 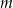 , dla których równanie
, dla których równanie
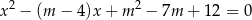
ma dwa różne rozwiązania rzeczywiste 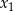 oraz
oraz 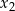 , spełniające warunek
, spełniające warunek
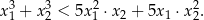
Wyznacz wszystkie wartości parametru 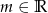 , dla których równanie
, dla których równanie 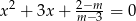 ma dwa różne pierwiastki
ma dwa różne pierwiastki 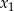 i
i 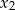 takie, że
takie, że 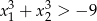 .
.
Wyznacz wszystkie wartości parametru 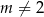 , dla których równanie
, dla których równanie
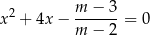
ma dwa różne rozwiązania rzeczywiste 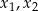 spełniające warunek
spełniające warunek 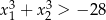 .
.
Wyznacz wszystkie wartości parametru 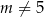 , dla których równanie
, dla których równanie
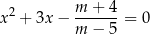
ma dwa różne rozwiązania rzeczywiste 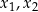 spełniające warunek
spełniające warunek 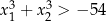 .
.
Wyznacz wszystkie wartości parametru 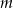 , dla których równanie
, dla których równanie 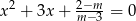 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 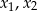 spełniające warunek
spełniające warunek 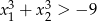 .
.
Na płaszczyźnie z prostokątnym układem współrzędnych zilustruj zbiór wszystkich punktów płaszczyzny o współrzędnych 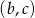 , takich, że równanie
, takich, że równanie 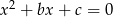 ma dwa różne rozwiązania należące do przedziału
ma dwa różne rozwiązania należące do przedziału 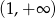 .
.
Liczby 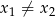 są dwoma dodatnimi pierwiastkami równania
są dwoma dodatnimi pierwiastkami równania 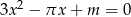 z niewiadomą
z niewiadomą  , gdzie
, gdzie 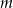 jest pewną ustaloną liczbą rzeczywistą.
jest pewną ustaloną liczbą rzeczywistą.
- Wykaż, że
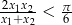 .
. - Wykaż, że
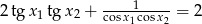 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 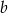 ,
,  równanie
równanie 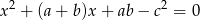 ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
ma co najmniej jedno rozwiązanie. Kiedy równanie ma dokładnie jedno rozwiązanie?
Nie rozwiązując równania 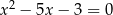 , oblicz sumę odwrotności czwartych potęg jego pierwiastków.
, oblicz sumę odwrotności czwartych potęg jego pierwiastków.
Oblicz sumę czwartych potęg pierwiastków równania 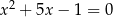 .
.
Dla jakich wartości parametru 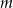 jeden z pierwiastków równania
jeden z pierwiastków równania 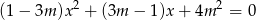 jest połową drugiego pierwiastka?
jest połową drugiego pierwiastka?
Wykaż, że dla dowolnej liczby rzeczywistej 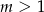 istnieje dokładnie jedna liczba rzeczywista
istnieje dokładnie jedna liczba rzeczywista  taka, że
taka, że
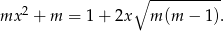
Wyznacz wszystkie wartości parametru 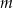 , dla których równanie
, dla których równanie
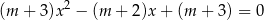
ma dwa różne rozwiązania 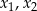 spełniające nierówność:
spełniające nierówność: 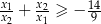 .
.

