Dla jakiej wartości parametru 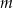 dwa różne pierwiastki
dwa różne pierwiastki 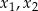 równania
równania
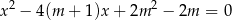
spełniają warunek 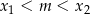 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla jakiej wartości parametru 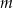 dwa różne pierwiastki
dwa różne pierwiastki 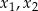 równania
równania
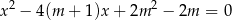
spełniają warunek 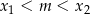 .
.
Wyznacz wszystkie wartości parametru 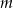 , dla których równanie
, dla których równanie 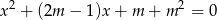 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 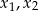 spełniające warunek:
spełniające warunek: 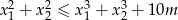 .
.
Wyznacz wszystkie wartości parametru 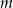 , dla których równanie
, dla których równanie 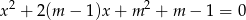 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 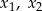 takie, że
takie, że 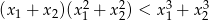 .
.
Dla jakich wartości parametru 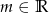 suma sześcianów dwóch różnych miejsc zerowych funkcji
suma sześcianów dwóch różnych miejsc zerowych funkcji 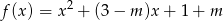 jest nieujemna?
jest nieujemna?
Wyznacz wszystkie wartości parametru 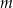 , dla których równanie
, dla których równanie
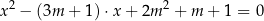
ma dwa różne rozwiązania rzeczywiste 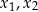 spełniające warunek
spełniające warunek
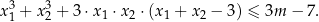
Wyznacz wszystkie wartości parametru 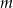 , dla których równanie
, dla których równanie 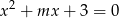 ma dwa różne pierwiastki rzeczywiste, takie, że suma ich czwartych potęg jest równa 82.
ma dwa różne pierwiastki rzeczywiste, takie, że suma ich czwartych potęg jest równa 82.
Wyznacz wszystkie wartości parametru 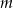 , dla których równanie
, dla których równanie 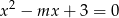 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 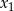 i
i 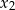 takie, że
takie, że 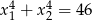 .
.
Wyznacz te wartości parametru 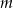 , dla których równanie
, dla których równanie 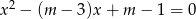 ma dwa rozwiązania
ma dwa rozwiązania 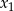 i
i 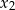 spełniające warunek
spełniające warunek 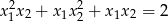 .
.
Dane jest równanie kwadratowe 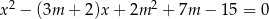 z niewiadomą
z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 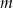 , dla których różne rozwiązania
, dla których różne rozwiązania 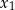 i
i 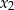 tego równania istnieją i spełniają warunek
tego równania istnieją i spełniają warunek
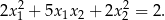
Dane jest równanie kwadratowe 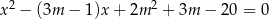 z niewiadomą
z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 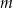 , dla których różne rozwiązania
, dla których różne rozwiązania 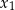 i
i 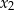 tego równania istnieją i spełniają warunek
tego równania istnieją i spełniają warunek
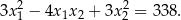
Wykaż, że funkcja kwadratowa 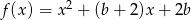 , ma co najmniej jedno miejsce zerowe dla każdej wartości parametru
, ma co najmniej jedno miejsce zerowe dla każdej wartości parametru 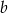 . Dla jakiej wartości parametru
. Dla jakiej wartości parametru 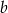 funkcja ma tylko jedno miejsce zerowe? Wyznacz to miejsce.
funkcja ma tylko jedno miejsce zerowe? Wyznacz to miejsce.
Uzasadnij, że równanie 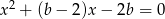 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej 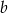 ma przynajmniej jedno rozwiązanie.
ma przynajmniej jedno rozwiązanie.
Dany jest trójmian kwadratowy 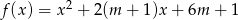 . Wyznacz wszystkie rzeczywiste wartości parametru
. Wyznacz wszystkie rzeczywiste wartości parametru 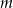 , dla których ten trójmian ma dwa różne pierwiastki
, dla których ten trójmian ma dwa różne pierwiastki 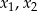 tego samego znaku, spełniające warunek
tego samego znaku, spełniające warunek 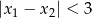 .
.
Dany jest trójmian kwadratowy 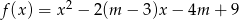 . Wyznacz wszystkie rzeczywiste wartości parametru
. Wyznacz wszystkie rzeczywiste wartości parametru 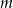 , dla których ten trójmian ma dwa różne pierwiastki
, dla których ten trójmian ma dwa różne pierwiastki 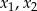 tego samego znaku, spełniające warunek
tego samego znaku, spełniające warunek 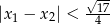 .
.
Wykaż, że jeżeli między współczynnikami trójmianów 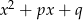 i
i 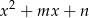 zachodzi związek
zachodzi związek 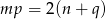 , to przynajmniej jedno z równań
, to przynajmniej jedno z równań 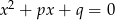 lub
lub 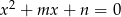 ma rozwiązanie.
ma rozwiązanie.
Wyznacz wszystkie wartości parametru 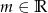 , dla których równanie
, dla których równanie 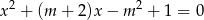 ma dwa różne pierwiastki
ma dwa różne pierwiastki 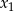 i
i 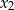 takie, że
takie, że 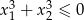 .
.
Wyznacz wszystkie wartości parametru 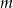 , dla których równanie
, dla których równanie 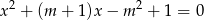 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 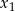 i
i 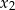
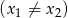 , spełniające warunek
, spełniające warunek 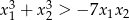 .
.
Dla jakich wartości parametru 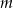 jeden pierwiastek równania
jeden pierwiastek równania 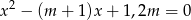 jest równy sinusowi, a drugi cosinusowi tego samego kąta ostrego?
jest równy sinusowi, a drugi cosinusowi tego samego kąta ostrego?
Uzasadnij, że dla dowolnej liczby całkowitej 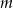 rozwiązania równania
rozwiązania równania 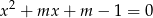 z niewiadomą
z niewiadomą  są liczbami całkowitymi.
są liczbami całkowitymi.
Wyznacz wszystkie wartości parametru 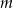 , dla których równanie
, dla których równanie
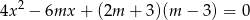
ma dwa różne rozwiązania rzeczywiste 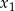 i
i 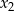 , przy czym
, przy czym 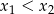 , spełniające warunek
, spełniające warunek
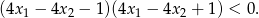
Wyznacz wszystkie wartości parametru 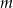 , dla których równanie
, dla których równanie
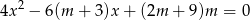
ma dwa różne rozwiązania rzeczywiste 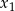 i
i 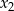 , przy czym
, przy czym 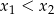 , spełniające warunek
, spełniające warunek
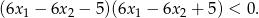
Wyznacz wszystkie wartości parametru 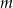 , dla których równanie
, dla których równanie 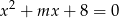 ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa
ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest równa 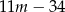 .
.
Wykaż, że funkcja kwadratowa 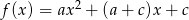 ma co najmniej jedno miejsce zerowe dla
ma co najmniej jedno miejsce zerowe dla 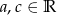 i
i 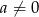 .
.
Liczby 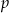 i
i 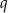 są pierwiastkami równania
są pierwiastkami równania 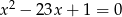 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia 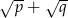 jest liczbą naturalną.
jest liczbą naturalną.
Dla jakich wartości parametru 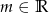 suma odwrotności kwadratów dwóch różnych miejsc zerowych funkcji
suma odwrotności kwadratów dwóch różnych miejsc zerowych funkcji 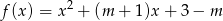 jest większa od 1?
jest większa od 1?
Wyznacz wszystkie wartości parametru 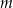 , dla których równanie
, dla których równanie
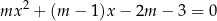
ma dokładnie dwa różne rozwiązania rzeczywiste 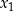 oraz
oraz 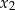 , spełniające warunki:
, spełniające warunki:
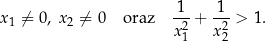
Wyznacz wszystkie wartości parametru 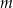 , dla których równanie
, dla których równanie
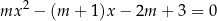
ma dokładnie dwa różne rozwiązania rzeczywiste 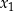 oraz
oraz 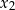 , spełniające warunki:
, spełniające warunki:
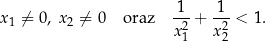
Wyznacz wszystkie wartości parametru 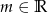 , dla których równanie
, dla których równanie 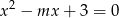 ma dwa różne pierwiastki
ma dwa różne pierwiastki 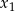 i
i 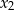 takie, że
takie, że 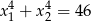 .
.
Suma współczynników 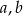 i
i  równania
równania 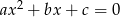 wynosi 24. Różnice
wynosi 24. Różnice 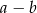 i
i 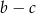 są równe, a jednym z rozwiązań równania jest liczba -3. Wyznacz drugie rozwiązanie.
są równe, a jednym z rozwiązań równania jest liczba -3. Wyznacz drugie rozwiązanie.
Wyznacz te wartości parametru 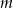 , dla których równanie
, dla których równanie 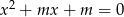 ma jedno rozwiązanie.
ma jedno rozwiązanie.
Wyznacz wszystkie wartości 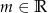 , dla których równanie
, dla których równanie 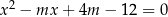 ma dwa różne pierwiastki spełniające nierówność
ma dwa różne pierwiastki spełniające nierówność
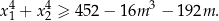
Dla jakiego parametru 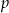 iloczyn miejsc zerowych funkcji
iloczyn miejsc zerowych funkcji 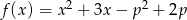 jest równy mniejszemu pierwiastkowi równania
jest równy mniejszemu pierwiastkowi równania 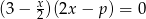 .
.
