Liczby 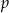 i
i 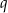 są pierwiastkami równania
są pierwiastkami równania 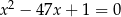 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia 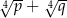 jest liczbą naturalną.
jest liczbą naturalną.
/Szkoła średnia/Równania/Kwadratowe
Rozwiąż równanie 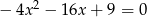 .
.
Rozwiąż równanie kwadratowe 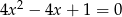 .
.
Rozwiąż równanie 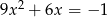 .
.
Rozwiąż równanie kwadratowe 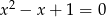 .
.
Rozwiąż równanie kwadratowe 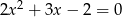 .
.
Rozwiąż równanie 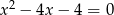 .
.
Wyznacz wszystkie wartości parametru 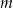 , dla których trójmian kwadratowy
, dla których trójmian kwadratowy
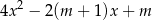
ma dwa różne pierwiastki rzeczywiste 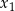 oraz
oraz 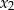 , spełniające warunki:
, spełniające warunki:
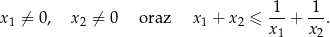
Wyznacz wszystkie wartości parametru 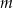 , dla których trójmian kwadratowy
, dla których trójmian kwadratowy
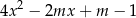
ma dwa różne pierwiastki rzeczywiste 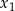 oraz
oraz 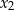 , spełniające warunki:
, spełniające warunki:
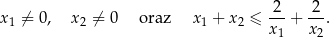
Rozwiązaniami równania 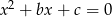 są liczby 8 i -3. Wyznacz parametry
są liczby 8 i -3. Wyznacz parametry 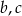 .
.
Funkcja kwadratowa o wzorze 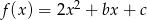 ma dwa miejsca zerowe
ma dwa miejsca zerowe 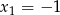 i
i 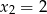 . Wyznacz wartość liczbową współczynników
. Wyznacz wartość liczbową współczynników 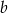 i
i  .
.
Funkcja kwadratowa o wzorze 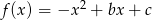 ma dwa miejsca zerowe
ma dwa miejsca zerowe 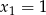 i
i 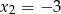 . Wyznacz wartość liczbową współczynników
. Wyznacz wartość liczbową współczynników 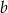 i
i  .
.
Dla jakich wartości parametru 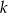 równanie
równanie 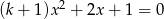 ma dwa rozwiązania przeciwnych znaków.
ma dwa rozwiązania przeciwnych znaków.
Wyznacz wszystkie wartości parametru 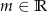 , dla których równanie
, dla których równanie
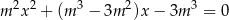
ma dwa różne rozwiązania rzeczywiste 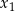 oraz
oraz 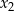 spełniające warunek
spełniające warunek
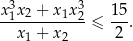
Wyznacz wszystkie wartości parametru 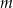 , dla których równanie
, dla których równanie
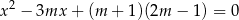
ma dwa różne rozwiązania 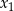 ,
, 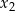 spełniające warunki:
spełniające warunki: 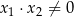 oraz
oraz 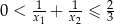 .
.
Wyznacz wszystkie wartości parametru 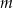 , dla których równanie
, dla których równanie
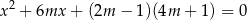
ma dwa różne rozwiązania 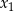 ,
, 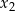 spełniające warunki:
spełniające warunki: 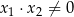 oraz
oraz 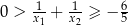 .
.
Liczby 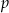 i
i 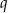 są pierwiastkami równania
są pierwiastkami równania 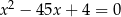 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia
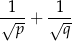
jest liczbą wymierną.
Wykaż że jeśli 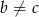 i funkcje kwadratowe
i funkcje kwadratowe 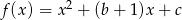 oraz
oraz 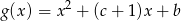 mają wspólne miejsce zerowe, to
mają wspólne miejsce zerowe, to 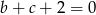 .
.
Liczby 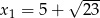 i
i 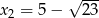 są rozwiązaniami równania
są rozwiązaniami równania 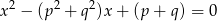 z niewiadomą
z niewiadomą  . Oblicz wartości
. Oblicz wartości 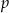 i
i 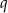 .
.
Przedyskutuj liczbę rozwiązań równania 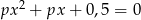 w zależności od wartości parametru
w zależności od wartości parametru 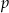 , a następnie naszkicuj wykres funkcji
, a następnie naszkicuj wykres funkcji 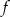 , która każdej wartości parametru
, która każdej wartości parametru 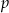 przyporządkowuje liczbę rozwiązań tego równania.
przyporządkowuje liczbę rozwiązań tego równania.
Dla jakich wartości parametru 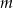 miejsca zerowe funkcji
miejsca zerowe funkcji 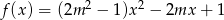 spełniają warunek
spełniają warunek 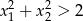 ?
?
Dla jakich wartości parametru  równanie
równanie 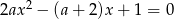 ma dwa różne pierwiastki, których suma jest liczbą z przedziału
ma dwa różne pierwiastki, których suma jest liczbą z przedziału 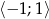 ?
?
Wyznacz wszystkie wartości parametru 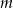 , dla których równanie
, dla których równanie 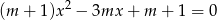 ma dwa różne pierwiastki takie, że ich suma jest nie większa niż 2,5.
ma dwa różne pierwiastki takie, że ich suma jest nie większa niż 2,5.
Liczby 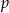 i
i 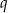 są pierwiastkami równania
są pierwiastkami równania 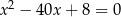 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia 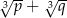 jest liczbą naturalną.
jest liczbą naturalną.
Dane jest równanie 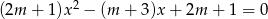 z niewiadomą
z niewiadomą  . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 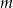 , dla których suma odwrotności różnych pierwiastków danego równania jest większa od 1.
, dla których suma odwrotności różnych pierwiastków danego równania jest większa od 1.
Wyznacz wszystkie wartości parametru 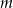 , dla których równanie
, dla których równanie 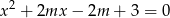 ma dwa różne pierwiastki należące do przedziału
ma dwa różne pierwiastki należące do przedziału 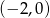 .
.
Dana jest funkcja kwadratowa 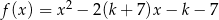 określona dla dowolnego
określona dla dowolnego 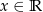 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 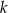 , dla których funkcja
, dla których funkcja 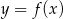 ma dwa różne miejsca zerowe należące do przedziału
ma dwa różne miejsca zerowe należące do przedziału 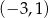 .
.
Wykaż, że jeżeli funkcje 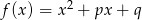 i
i 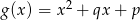 , gdzie
, gdzie 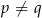 , mają wspólne miejsce zerowe, to
, mają wspólne miejsce zerowe, to 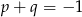 .
.
Wyznacz te wartości parametru 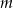 , dla których równanie
, dla których równanie 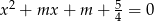 ma dwa różne pierwiastki ujemne.
ma dwa różne pierwiastki ujemne.
Wyznacz te wartości parametru 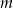 , dla których równanie
, dla których równanie 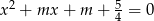 ma dwa różne pierwiastki nieujemne.
ma dwa różne pierwiastki nieujemne.
Wyznacz wszystkie wartości parametru 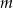 , dla których dwa różne pierwiastki rzeczywiste
, dla których dwa różne pierwiastki rzeczywiste 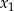 i
i 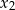 równania
równania 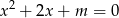 spełniają nierówność
spełniają nierówność 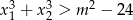 .
.
Liczby  i
i 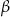 są pierwiastkami równania
są pierwiastkami równania 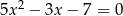 . Wykaż, że pierwiastkami równania
. Wykaż, że pierwiastkami równania 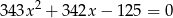 są liczby
są liczby 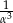 i
i 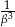 .
.
Liczby 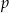 i
i 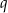 są pierwiastkami równania
są pierwiastkami równania 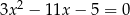 . Wykaż, że pierwiastkami równania
. Wykaż, że pierwiastkami równania 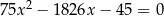 są liczby
są liczby 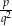 i
i 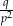 .
.

