Wyznacz wszystkie wartości parametru 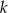 , dla których równanie
, dla których równanie
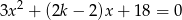
ma dwa różne rozwiązania rzeczywiste 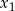 i
i 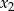 , przy czym
, przy czym 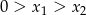 , spełniające warunek
, spełniające warunek
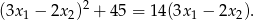
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie wartości parametru 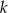 , dla których równanie
, dla których równanie
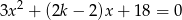
ma dwa różne rozwiązania rzeczywiste 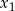 i
i 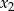 , przy czym
, przy czym 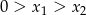 , spełniające warunek
, spełniające warunek
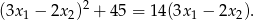
Dla jakich wartości parametru 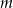 liczba 1 zawiera się między różnymi pierwiastkami równania
liczba 1 zawiera się między różnymi pierwiastkami równania 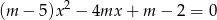 ?
?
Podaj miejsca zerowe funkcji 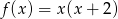 .
.
Wyznacz miejsce zerowe funkcji 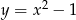 .
.
Podaj miejsca zerowe funkcji 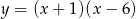 .
.
Podaj miejsca zerowe funkcji 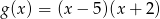 .
.
Podaj miejsca zerowe funkcji 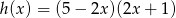 .
.
Wyznacz wszystkie wartości parametru 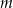 , dla których równanie
, dla których równanie 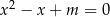 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 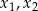 spełniające warunek
spełniające warunek 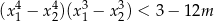 .
.
Liczby  i
i 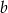 są rozwiązaniami równania
są rozwiązaniami równania 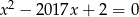 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
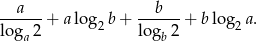
Liczby  i
i 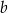 są rozwiązaniami równania
są rozwiązaniami równania 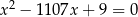 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
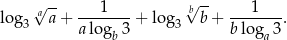
Rozwiąż równanie: 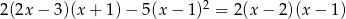 .
.
Rozwiąż równanie: 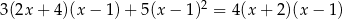 .
.
Wykaż, że jeżeli 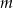 i
i  są takimi liczbami całkowitymi, że rozwiązania równania
są takimi liczbami całkowitymi, że rozwiązania równania 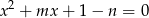 są niezerowymi liczbami całkowitymi, to liczba
są niezerowymi liczbami całkowitymi, to liczba 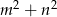 nie jest liczbą pierwszą.
nie jest liczbą pierwszą.
Dla jakich całkowitych wartości parametru 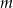 pierwiastkami równania
pierwiastkami równania 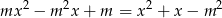 są liczby całkowite?
są liczby całkowite?
Liczby 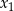 i
i 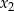 są wszystkimi pierwiastkami rzeczywistymi równania
są wszystkimi pierwiastkami rzeczywistymi równania 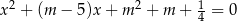 , przy czym zakładamy, że
, przy czym zakładamy, że 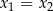 w przypadku, gdy równanie ma tylko jedno rozwiązanie. Zbadaj, dla jakich wartości parametru
w przypadku, gdy równanie ma tylko jedno rozwiązanie. Zbadaj, dla jakich wartości parametru 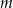 , wyrażenie
, wyrażenie 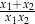 przyjmuje wartość najmniejszą. Oblicz tę wartość.
przyjmuje wartość najmniejszą. Oblicz tę wartość.
Wyznacz wszystkie wartości parametru 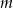 , dla których równanie
, dla których równanie 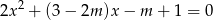 ma dwa różne pierwiastki
ma dwa różne pierwiastki 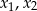 takie, że
takie, że 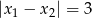 .
.
Funkcja kwadratowa 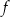 jest określona wzorem
jest określona wzorem 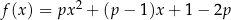 dla każdego
dla każdego 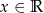 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 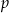 , dla których funkcja
, dla których funkcja 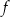 ma dokładnie dwa miejsca zerowe różniące się o 1.
ma dokładnie dwa miejsca zerowe różniące się o 1.
Wyznacz wszystkie wartości parametru 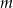 , dla których równanie
, dla których równanie 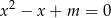 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 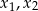 spełniające warunek
spełniające warunek 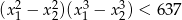 .
.
Dane jest równanie 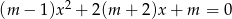 z niewiadomą
z niewiadomą  .
.
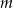 .
. 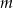 zachodzi nierówność
zachodzi nierówność 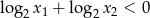 , gdzie
, gdzie 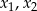 są różnymi pierwiastkami danego równania.
są różnymi pierwiastkami danego równania.Wyznacz te wartości parametru 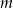 , dla których równanie
, dla których równanie 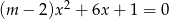 ma jedno rozwiązanie.
ma jedno rozwiązanie.
Wyznacz wszystkie takie wartości parametru 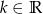 , aby liczba 2 znajdowała się między miejscami zerowymi funkcji
, aby liczba 2 znajdowała się między miejscami zerowymi funkcji 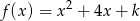 .
.
Miejscami zerowymi trójmianu kwadratowego 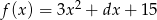 są liczby całkowite. Oblicz
są liczby całkowite. Oblicz 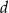 .
.
Dla jakich 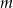 równanie
równanie 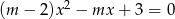 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
Wyznacz wszystkie liczby 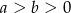 takie, że
takie, że 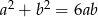 .
.
Wyznacz te wartości parametru 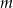 , dla których równanie
, dla których równanie 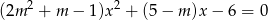 ma dwa różne pierwiastki tego samego znaku.
ma dwa różne pierwiastki tego samego znaku.
Wyznacz wszystkie wartości parametru 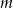 , dla których funkcja kwadratowa
, dla których funkcja kwadratowa 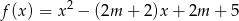 ma dwa różne pierwiastki
ma dwa różne pierwiastki 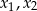 takie, że suma kwadratów odległości punktów
takie, że suma kwadratów odległości punktów 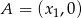 i
i 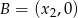 od prostej o równaniu
od prostej o równaniu 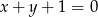 jest równa 6.
jest równa 6.
Wyznacz wszystkie wartości parametru 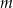 , dla których równanie
, dla których równanie 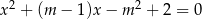 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 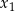 i
i 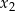
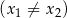 , spełniające warunek
, spełniające warunek 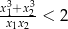 .
.
