Dane jest równanie 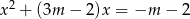 z niewiadomą
z niewiadomą  . Sformułuj warunki, jakie powinien spełniać parametr
. Sformułuj warunki, jakie powinien spełniać parametr 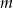 , by to równanie miało dwa różne pierwiastki, których suma odwrotności jest dodatnia.
, by to równanie miało dwa różne pierwiastki, których suma odwrotności jest dodatnia.
/Szkoła średnia/Równania/Kwadratowe
Dane jest równanie 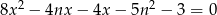 z niewiadomą
z niewiadomą  i parametrem
i parametrem  .
.
- Wyznacz wszystkie wartości
 , dla których suma odwrotności pierwiastków tego równania jest równa
, dla których suma odwrotności pierwiastków tego równania jest równa 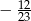 .
. - Wykaż, że jeżeli
 jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
Wyznacz te wartości parametru 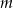 , dla których prosta
, dla których prosta 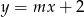 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 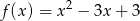 .
.
Wyznacz te wartości parametru 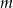 , dla których prosta
, dla których prosta 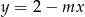 nie ma punktów wspólnych z wykresem funkcji
nie ma punktów wspólnych z wykresem funkcji 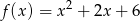 .
.
Wyznacz te wartości parametru 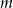 , dla których prosta
, dla których prosta 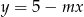 ma dwa punkty wspólne z wykresem funkcji
ma dwa punkty wspólne z wykresem funkcji 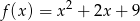 .
.
Wyznacz te wartości parametru 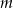 , dla których prosta
, dla których prosta 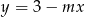 ma jeden punkt wspólny z wykresem funkcji
ma jeden punkt wspólny z wykresem funkcji 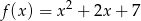 .
.
Wyznacz te wartości parametru 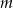 , dla których prosta
, dla których prosta 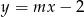 ma jeden punkt wspólny z wykresem funkcji
ma jeden punkt wspólny z wykresem funkcji 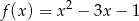 .
.
Wyznacz te wartości parametru 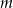 , dla których prosta
, dla których prosta 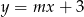 ma dwa punkty wspólne z wykresem funkcji
ma dwa punkty wspólne z wykresem funkcji 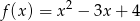 .
.
Dla jakich wartości parametru 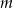 suma pierwiastków równania
suma pierwiastków równania 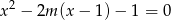 jest równa sumie kwadratów tych pierwiastków?
jest równa sumie kwadratów tych pierwiastków?
Określ, jakie znaki mają pierwiastki równania kwadratowego wiedząc, że suma pierwiastków równania jest równa 2 oraz suma kwadratów pierwiastków była równa 16.
Wyznacz wszystkie liczby 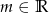 , dla których równanie
, dla których równanie 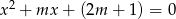 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 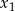 i
i 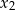 takie, że
takie, że 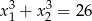 .
.
Wyznacz wszystkie liczby 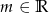 , dla których równanie
, dla których równanie 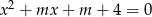 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 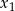 i
i 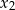 takie, że
takie, że 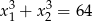 .
.
Oblicz wszystkie wartości parametru 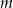 , dla których równanie
, dla których równanie 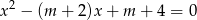 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 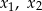 takie, że
takie, że 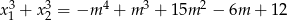 .
.
Wyznacz tę wartość parametru 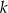 , dla której suma kwadratów dwóch różnych pierwiastków równania
, dla której suma kwadratów dwóch różnych pierwiastków równania 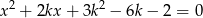 jest największa z możliwych.
jest największa z możliwych.
Dla jakich wartości parametru 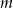 suma kwadratów dwóch różnych pierwiastków równania
suma kwadratów dwóch różnych pierwiastków równania 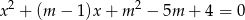 przyjmuje wartość największą. Wyznacz tę wartość.
przyjmuje wartość największą. Wyznacz tę wartość.
Dla jakich wartości parametru 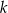 suma kwadratów pierwiastków równania
suma kwadratów pierwiastków równania 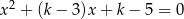 jest najmniejsza?
jest najmniejsza?
Liczby 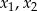 są takimi rozwiązaniami równania
są takimi rozwiązaniami równania 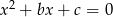
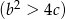 , że
, że 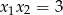 i
i 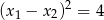 . Oblicz
. Oblicz 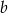 i
i  .
.
Wyznacz wszystkie liczby naturalne dodatnie 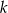 , dla których równanie
, dla których równanie 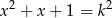 ma pierwiastki będące liczbami całkowitymi.
ma pierwiastki będące liczbami całkowitymi.
Dla jakich wartości parametru 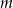 równanie
równanie 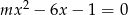 ma co najmniej jedno rozwiązanie?
ma co najmniej jedno rozwiązanie?
Dane są liczby wymierne 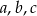 takie, że równanie
takie, że równanie 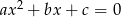 ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.
ma dwa rozwiązania rzeczywiste. Uzasadnij, że jeżeli jeden z pierwiastków tego równania jest liczbą wymierną to drugi pierwiastek też jest liczbą wymierną.
Dane są niezerowe liczby wymierne 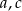 takie, że funkcja
takie, że funkcja 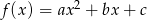 ma miejsce zerowe będące liczbą wymierną. Wykaż, że
ma miejsce zerowe będące liczbą wymierną. Wykaż, że 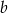 jest liczbą wymierną.
jest liczbą wymierną.
Dla jakich wartości parametru 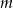 równanie
równanie 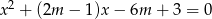 ma dwa różne pierwiastki
ma dwa różne pierwiastki 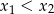 spełniające nierówność
spełniające nierówność 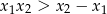 .
.
Wyznacz te wartości parametru 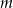 , dla których równanie
, dla których równanie 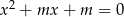 ma takie dwa różne pierwiastki, że suma ich kwadratów jest mniejsza od 15.
ma takie dwa różne pierwiastki, że suma ich kwadratów jest mniejsza od 15.
Wyznacz wszystkie wartości parametru 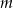 , dla których równanie
, dla których równanie 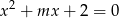 ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest większa od
ma dwa różne pierwiastki rzeczywiste takie, że suma ich kwadratów jest większa od 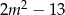 .
.
Znajdź zbiór tych wartości parametru 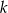 , dla których dane równanie ma dwa różne pierwiastki
, dla których dane równanie ma dwa różne pierwiastki 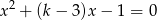 .
.
Ułóż równanie kwadratowe, takie, by suma pierwiastków równania była równa 5 oraz aby kwadrat różnicy tych pierwiastków był równy 37.
Ułóż równanie kwadratowe, takie, by iloczyn pierwiastków równania był równy 4 oraz by suma odwrotności kwadratów jego pierwiastków była równa 2.
Ułóż równanie kwadratowe, takie, by suma pierwiastków równania była równa 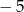 oraz by suma odwrotności jego pierwiastków była równa 10.
oraz by suma odwrotności jego pierwiastków była równa 10.
Oblicz sumę szóstych potęg pierwiastków równania 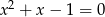 .
.
Wyznacz wszystkie wartości parametru 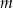 , dla których równanie
, dla których równanie
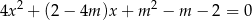
ma dwa różne dodatnie rozwiązania 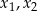 spełniające nierówność
spełniające nierówność 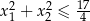 .
.
Wyznacz wszystkie wartości parametru 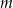 , dla których równanie
, dla których równanie
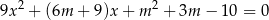
ma dwa różne ujemne rozwiązania 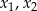 spełniające nierówność
spełniające nierówność 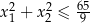 .
.
Dla jakich 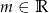 równanie
równanie 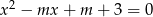 ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 1?
ma dwa różne rozwiązania, których suma odwrotności jest mniejsza od 1?
Wyznacz wszystkie wartości 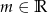 , dla których równanie
, dla których równanie 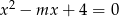 ma dwa różne pierwiastki spełniające nierówność
ma dwa różne pierwiastki spełniające nierówność 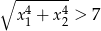 .
.
Dany jest trójmian kwadratowy 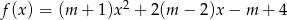 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 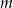 , dla których trójmian
, dla których trójmian 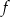 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 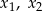 , spełniające warunek
, spełniające warunek 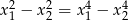 .
.
Dany jest trójmian kwadratowy 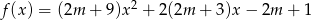 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 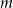 , dla których trójmian
, dla których trójmian 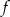 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 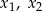 , spełniające warunek
, spełniające warunek 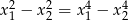 .
.

