Na jednym z ramion kąta ostrego o wierzchołku 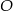 i mierze
i mierze  wybrano punkty
wybrano punkty 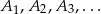 , a na drugim ramieniu punkty
, a na drugim ramieniu punkty 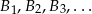 w ten sposób, że
w ten sposób, że 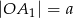 ,
, 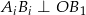 oraz
oraz 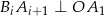 dla wszystkich
dla wszystkich 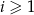 .
.
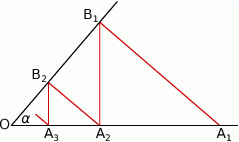
Wykaż, że długość nieskończonej łamanej 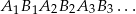 jest równa
jest równa 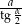 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na jednym z ramion kąta ostrego o wierzchołku 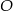 i mierze
i mierze  wybrano punkty
wybrano punkty 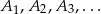 , a na drugim ramieniu punkty
, a na drugim ramieniu punkty 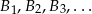 w ten sposób, że
w ten sposób, że 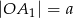 ,
, 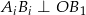 oraz
oraz 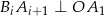 dla wszystkich
dla wszystkich 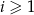 .
.

Wykaż, że długość nieskończonej łamanej 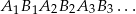 jest równa
jest równa 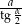 .
.
Wykaż, że zbiór 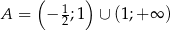 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
Wykaż, że suma szeregu geometrycznego zbieżnego jest ujemna wtedy i tylko wtedy, gdy jego pierwszy wyraz jest ujemny.
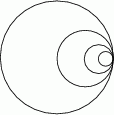
Dany jest okrąg  o promieniu
o promieniu  . Wewnątrz tego okręgu narysowano okrąg
. Wewnątrz tego okręgu narysowano okrąg  styczny wewnętrznie o średnicy
styczny wewnętrznie o średnicy  , wewnątrz okręgu
, wewnątrz okręgu  znów narysowano okrąg styczny wewnętrznie o średnicy
znów narysowano okrąg styczny wewnętrznie o średnicy 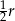 itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów
itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów 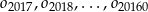 jest mniejsza od długości okręgu
jest mniejsza od długości okręgu 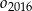 .
.
Dany jest nieskończony ciąg geometryczny 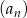 określony dla
określony dla 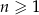 , w którym
, w którym 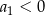 . Suma
. Suma 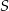 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 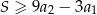 . Wykaż, ze
. Wykaż, ze 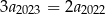 .
.
Dany jest nieskończony ciąg geometryczny 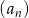 , który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym
, który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym 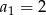 , oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu
, oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu 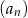 jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
Na płaszczyźnie dany jest nieskończony ciąg 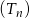 , dla
, dla 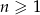 , równoramiennych trójkątów prostokątnych. Pole trójkąta
, równoramiennych trójkątów prostokątnych. Pole trójkąta 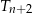 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 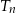 dla
dla 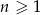 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 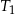 i
i 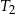 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Na płaszczyźnie dany jest nieskończony ciąg 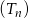 , dla
, dla 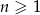 , trójkątów równobocznych. Pole trójkąta
, trójkątów równobocznych. Pole trójkąta 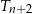 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 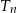 dla
dla 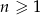 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 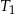 i
i 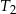 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
