Trygonometryczne/Udowodnij... - zadania z matematyki

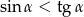/Szkoła średnia/Nierówności/Udowodnij.../Trygonometryczne

Udowodnij, że dla dowolnego kąta ostrego prawdziwa jest nierówność sin α < tg α .

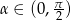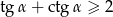Wykaż, że dla każdej liczby π- α ∈ (0,2 ) zachodzi nierówność tgα + ctg α ≥ 2 .

Udowodnij, że dla dowolnego kąta 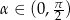π- α ∈ (0,2) prawdziwa jest nierówność

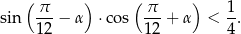
( π ) ( π ) 1 sin ---− α ⋅cos ---+ α < -. 12 12 4

Ukryj Podobne zadania

Udowodnij, że dla dowolnego kąta 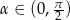π- α ∈ (0,2) prawdziwa jest nierówność

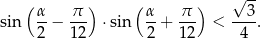
( ) ( ) √ -- sin α-− π-- ⋅sin α-+ π-- < --3. 2 12 2 12 4

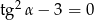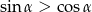Wykaż, że jeżeli jest kątem ostrym spełniającym warunek 2 tg α− 3 = 0 to sin α > co sα .

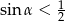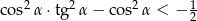Wykaż, że jeżeli jest kątem ostrym oraz 1 sin α < 2 to 2 2 2 1 co s α ⋅tg α − cos α < − 2 .