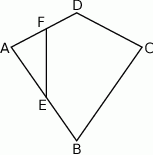
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest trójkąt prostokątny. Długość jednej z przyprostokątnych jest równa 8 cm, a długość przeciwprostokątnej jest równa 10 cm. Najmniejsza ściana boczna tego graniastosłupa ma pole równe 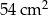 .
.

Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.

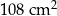 .
. 
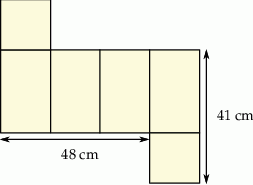
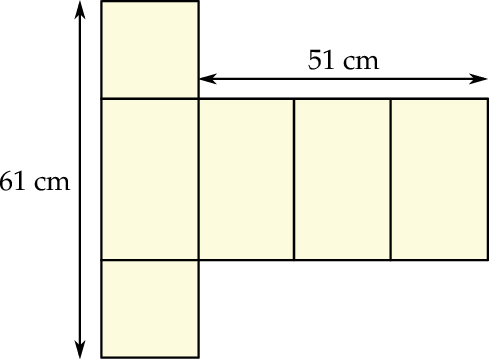
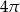 . Oblicz pole kwadratu.
. Oblicz pole kwadratu. 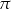 .
. 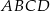 i
i 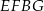 o bokach długości 5 cm i 13 cm. Oblicz długość odcinka
o bokach długości 5 cm i 13 cm. Oblicz długość odcinka 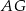 .
. 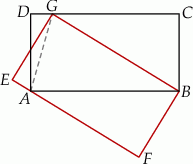
 punkt
punkt  jest takim punktem boku
jest takim punktem boku  , że
, że 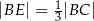 . Z wierzchołka
. Z wierzchołka 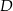 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 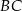 w punkcie
w punkcie 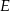 . Proste
. Proste 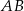 i
i 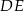 przecinają się w punkcie
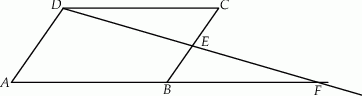
przecinają się w punkcie 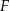 (zobacz rysunek). Wykaż, że pole trójkąta
(zobacz rysunek). Wykaż, że pole trójkąta 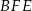 stanowi
stanowi 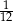 pola równoległoboku
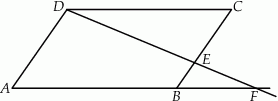
pola równoległoboku 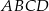 .
. 
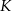 i
i 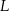 dzielą podstawę
dzielą podstawę 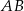 trapezu
trapezu 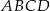 na trzy równe części, a punkty
na trzy równe części, a punkty 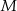 i
i 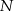 dzielą podstawę
dzielą podstawę 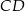 tego trapezu na trzy równe części. Pole czworokąta
tego trapezu na trzy równe części. Pole czworokąta 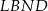 jest równe
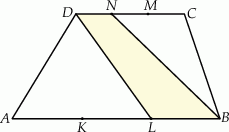
jest równe 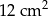 . Oblicz pole trapezu
. Oblicz pole trapezu 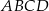 .
. 

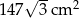 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 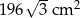 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. 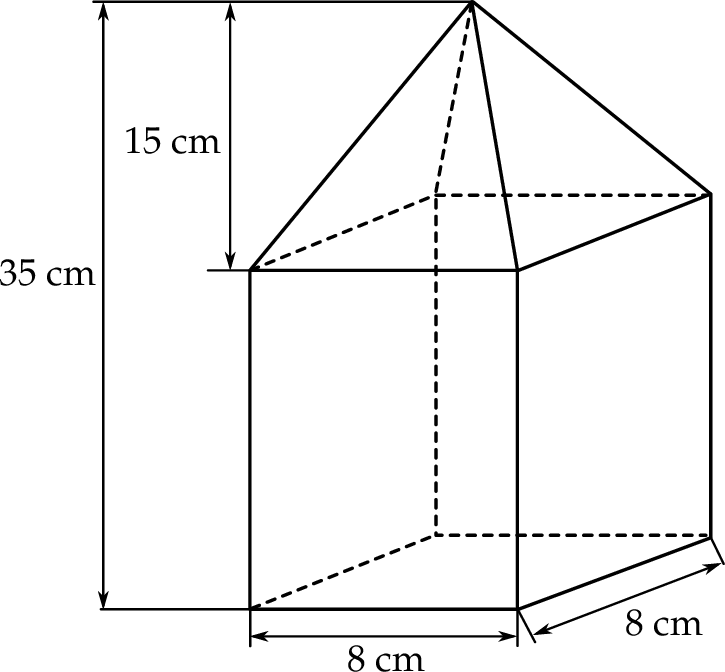
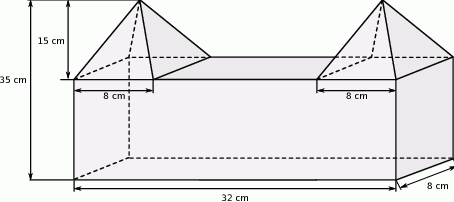
 dane są:
dane są: 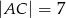 ,
, 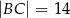 i
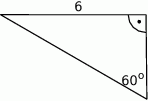
i 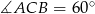 . Oblicz pole trójkąta
. Oblicz pole trójkąta 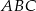 .
. 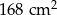 . Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
. Oblicz objętość tego graniastosłupa. Zapisz obliczenia. 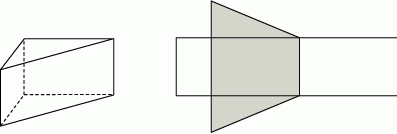
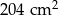 . Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
. Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia. 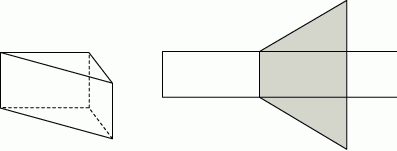
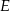 jest środkiem boku
jest środkiem boku 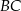 równoległoboku
równoległoboku 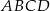 , a odcinek
, a odcinek  przecina przekątną
przecina przekątną 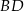 w punkcie
w punkcie 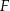 . Wykaż, że
. Wykaż, że 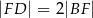 .
. 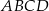 punkt
punkt 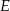 jest środkiem boku
jest środkiem boku 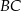 . Z wierzchołka
. Z wierzchołka 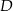 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 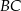 w punkcie
w punkcie 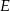 . Proste
. Proste 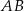 i
i 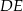 przecinają się w punkcie
przecinają się w punkcie 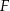 (zobacz rysunek). Wykaż, że punkt
(zobacz rysunek). Wykaż, że punkt 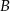 jest środkiem odcinka
jest środkiem odcinka 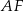 .
. 
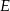 i
i 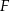 są środkami boków
są środkami boków 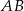 i
i 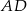 deltoidu
deltoidu 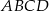 . Pole trójkąta
. Pole trójkąta 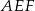 jest równe 3. Oblicz pole deltoidu
jest równe 3. Oblicz pole deltoidu 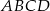 .
.