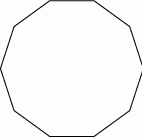
Ile można utworzyć trójkątów równoramiennych, których wierzchołki są jednocześnie wierzchołkami ustalonego dziesięciokąta foremnego?
/Szkoła średnia/Kombinatoryka/Geometryczne
Na jednej prostej zaznaczono 3 punkty, a na drugiej 4 punkty.
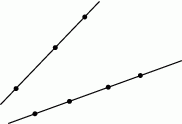
Ile jest wszystkich trójkątów, których wierzchołkami są trzy spośród zaznaczonych punktów?
Pojedynczy znak w piśmie Braille’a dla niewidomych jest kombinacją od 1 do 6 wypukłych punktów, które mogą zajmować miejsca ułożone w dwóch kolumnach po trzy miejsca w każdej kolumnie. Poniżej podano przykład napisu w piśmie Braille’a. Czarne kropki w znaku oznaczają wypukłości, a białe kropki oznaczają brak wypukłości. Pojedynczy znak w piśmie Braille’a musi zawierać co najmniej jeden punkt wypukły.
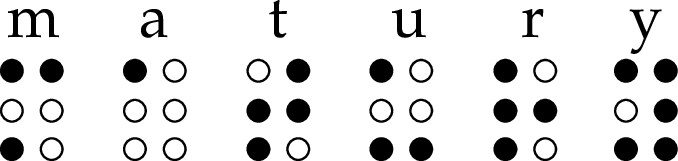
Oblicz, ile różnych pojedynczych znaków można zapisać w piśmie Braille’a.
W pewnym mieście jest prostopadły układ ulic, a ruch na każdej z nich jest dwukierunkowy. W centrum miasta znajduje się park, gdzie obowiązuje całkowity zakaz ruchu pojazdów. Schemat ulic w tym mieście wraz z położeniem parku przedstawiono poniżej na rysunku. Tomek znajduje się w punkcie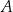 
miasta i chce dojechać samochodem najkrótszą drogą do punktu 
.
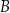Oblicz, ile jest najkrótszych dróg z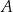 
do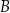 
.
Na okręgu zaznaczono sześć różnych punktów. Ile różnych wielokątów wypukłych o wszystkich wierzchołkach w tych punktach można narysować?
Na płaszczyźnie danych jest 100 punktów, z których żadne 3 nie leżą na jednej prostej. Ile jest różnych trójkątów o wierzchołkach w tych punktach?
Ukryj
Podobne zadania
Na okręgu wybrano 50 punktów. Ile jest różnych czworokątów o wierzchołkach w tych punktach?
Okrąg podzielono dwudziestoma punktami na dwadzieścia łuków tej samej długości. Ile można zbudować łamanych zamkniętych z wierzchołkami w tych punktach i z odcinkami równej długości? (Odcinki mogą się przecinać, ale nie mogą się pokrywać.)
Proste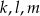 
są parami różne i równoległe. Na prostych tych wybrano zbiór 
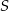składający się z 
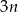punktów (
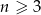), przy czym na każdej z prostych wybrano 
punktów. Wiadomo ponadto, że jeżeli trzy punkty zbioru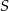 
leżą na jednej prostej, to prostą tą jest 
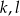lub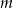 
. Oblicz ile jest trójkątów o wierzchołkach należących do zbioru 
.
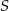