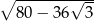Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 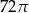 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 6 B) 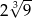 C) 12 D)
C) 12 D) 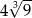
/Szkoła średnia/Zadania testowe
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 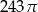 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 9 B) 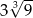 C)
C) 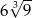 D) 18
D) 18
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 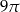 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 6 B) 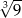 C) 3 D)
C) 3 D) 
Punkty 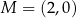 i
i 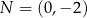 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 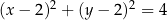 B)
B) 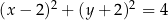
C) 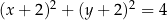 D)
D) 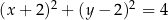
Punkty 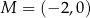 i
i 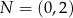 są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
są punktami styczności okręgu z osiami układu współrzędnych. Które z poniższych równań opisuje ten okrąg?
A) 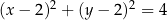 B)
B) 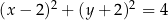
C) 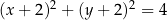 D)
D) 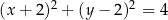
Funkcja liniowa 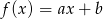 jest rosnąca i ma dodatnie miejsce zerowe. Stąd wynika, że
jest rosnąca i ma dodatnie miejsce zerowe. Stąd wynika, że
A) 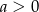 i
i 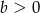 B)
B) 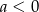 i
i 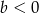 C)
C) 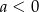 i
i 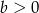 D)
D) 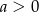 i
i 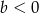
Funkcja liniowa 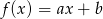 jest malejąca i ma dodatnie miejsce zerowe. Stąd wynika, że
jest malejąca i ma dodatnie miejsce zerowe. Stąd wynika, że
A) 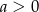 i
i 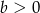 B)
B) 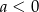 i
i 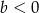 C)
C) 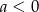 i
i 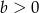 D)
D) 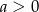 i
i 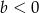
Wartością wyrażenia 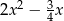 dla
dla 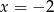 jest liczba:
jest liczba:
A) 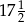 B)
B) 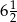 C)
C) 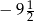 D)
D) 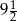
Ciąg 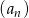 jest rosnącym ciągiem geometrycznym o ilorazie
jest rosnącym ciągiem geometrycznym o ilorazie 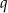 , gdzie
, gdzie 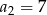 i
i 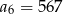 . Zatem:
. Zatem:
A) 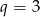 lub
lub 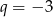 B)
B) 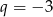 C)
C) 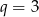 D)
D) 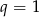
Trzeci wyraz pewnego ciągu geometrycznego jest równy 6, a szósty wyraz ma wartość 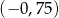 . Iloraz tego ciągu jest równy:
. Iloraz tego ciągu jest równy:
A) 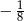 B)
B) 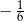 C)
C) 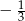 D)
D) 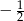
Liczba 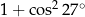 jest równa
jest równa
A)  B)
B) 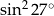 C)
C)  D) 2
D) 2
Klient banku wypłacił z bankomatu kwotę 1040 zł. Bankomat wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było dwa razy więcej niż 50–złotowych, a banknotów 20–złotowych było o 2 mniej niż 50–złotowych. Niech  oznacza liczbę banknotów 50–złotowych, a
oznacza liczbę banknotów 50–złotowych, a 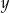 – liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb
– liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb  i
i 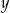 to
to
A) 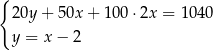 B)
B) 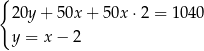
C) 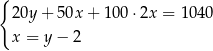 D)
D) 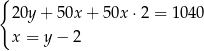
Tomek ma w skarbonce wyłącznie monety dwuzłotowe i pięciozłotowe. W sumie ma w skarbonce 351 zł. Gdyby dołożył do skarbonki 10 monet pięciozłotowych i dwie monety dwuzłotowe, to miałby w skarbonce dwa razy więcej monet dwuzłotowych, niż monet pięciozłotowych. Jeżeli oznaczymy przez  liczbę monet pięciozłotowych, a przez
liczbę monet pięciozłotowych, a przez 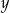 liczbę monet dwuzłotowych w skarbonce Tomka, to liczby
liczbę monet dwuzłotowych w skarbonce Tomka, to liczby  i
i 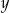 spełniają układ równań
spełniają układ równań
A) 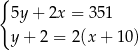 B)
B) 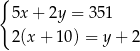
C) 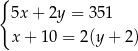 D)
D) 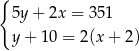
Klient banku wypłacił z bankomatu kwotę 1680 zł. Bankomat wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było o 50% więcej niż 50–złotowych, a banknotów 20–złotowych było o 50% mniej niż 50–złotowych. Niech  oznacza liczbę banknotów 50–złotowych, a
oznacza liczbę banknotów 50–złotowych, a 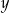 – liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb
– liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb  i
i 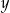 to
to
A) 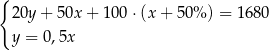 B)
B) 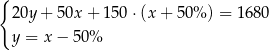
C) 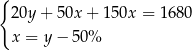 D)
D) 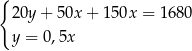
Liczba rozwiązań równania 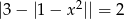 jest równa
jest równa
A) 6 B) 4 C) 2 D) 5
Przedstawione na rysunku trójkąty są podobne.
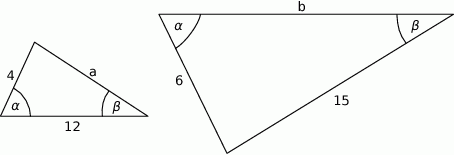
Wówczas
A) 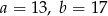 B)
B) 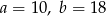 C)
C) 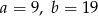 D)
D) 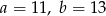
Przedstawione na rysunku trójkąty 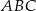 i
i 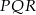 są podobne. Bok
są podobne. Bok 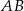 trójkąta
trójkąta  ma długość
ma długość
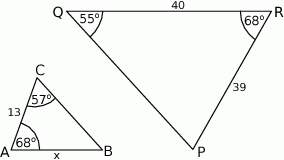
A) 14 B) 16 C) 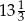 D) 12
D) 12
Przedstawione na rysunku trójkąty  i
i 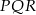 są podobne. Bok
są podobne. Bok 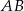 trójkąta
trójkąta 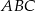 ma długość
ma długość
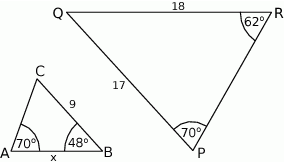
A) 8 B) 8,5 C) 9,5 D) 10
Wszystkich różnych liczb naturalnych trzycyfrowych, w których zapisie dziesiętnym przynajmniej jedna cyfra występuje dwa razy jest
A) 252 B) 180 C) 171 D) 396
Rozwiązaniem równania 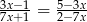 jest
jest
A) 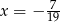 B)
B) 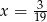 C)
C) 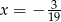 D)
D) 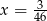
Rozwiązaniem równania 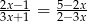 jest
jest
A) 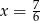 B)
B) 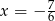 C)
C) 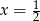 D)
D) 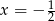
Dany jest trapez 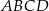 , w którym
, w którym 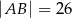 ,
, 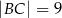 ,
, 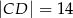 i
i 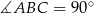 (zobacz rysunek).
(zobacz rysunek).
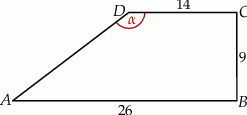
Stąd wynika, że cosinus zaznaczonego na rysunku kąta  jet równy
jet równy
A)  B)
B) 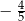 C)
C) 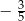 D)
D) 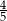
Dana jest nierówność kwadratowa
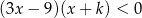
z niewiadomą  i parametrem
i parametrem 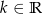 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 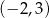 . Liczba
. Liczba 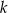 jest równa
jest równa
A) 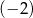 B) 2 C)
B) 2 C) 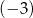 D) 3
D) 3
Dana jest nierówność kwadratowa
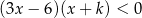
z niewiadomą  i parametrem
i parametrem 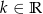 . Rozwiązaniem tej nierówności jest przedział
. Rozwiązaniem tej nierówności jest przedział 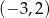 . Liczba
. Liczba 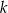 jest równa
jest równa
A) 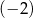 B) 2 C)
B) 2 C) 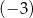 D) 3
D) 3
Punkty 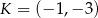 i
i 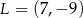 są środkami boków
są środkami boków 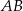 i
i 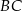 prostokąta
prostokąta 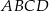 . Boki prostokąta
. Boki prostokąta 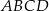 są równoległe do osi układu współrzędnych. Pole prostokąta
są równoległe do osi układu współrzędnych. Pole prostokąta 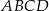 jest równe.
jest równe.
A) 48 B) 20 C) 192 D) 400
Funkcja 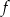 przyporządkowuje każdej liczbie naturalnej większej od 1 sumę jej cyfr. Liczba
przyporządkowuje każdej liczbie naturalnej większej od 1 sumę jej cyfr. Liczba  dla której prawdziwa jest równość
dla której prawdziwa jest równość
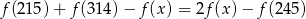
może być równa
A) 2114 B) 3115 C) 1611 D) 4103
Pięć spośród sześciu różnokolorowych kul wkładamy do pięciu ponumerowanych szuflad tak, że w każdej szufladzie znajduje się jedna kula. Na ile różnych sposobów można to zrobić?
A) 120 B) 720 C) 24 D) 126
Ciąg 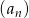 spełnia warunek
spełnia warunek 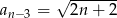 dla
dla 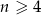 . Wówczas
. Wówczas
A) 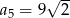 B)
B) 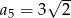 C)
C) 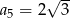 D)
D) 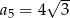
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 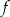 określonej wzorem
określonej wzorem 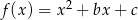 .
.
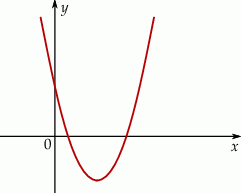
Współczynniki 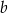 i
i  spełniają warunki:
spełniają warunki:
A) 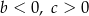 B)
B) 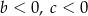 C)
C) 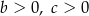 D)
D) 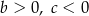
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 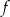 określonej wzorem
określonej wzorem 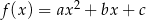 .
.
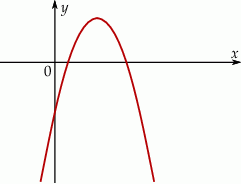
Współczynniki 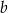 i
i  spełniają warunki:
spełniają warunki:
A) 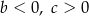 B)
B) 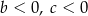 C)
C) 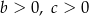 D)
D) 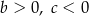
Na rysunku jest przedstawiona prosta zawierająca przekątną 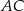 rombu
rombu 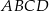 oraz wierzchołki
oraz wierzchołki 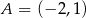 i
i 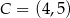 tego rombu.
tego rombu.
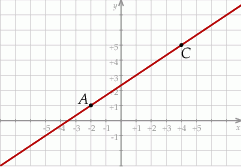
Wskaż równanie prostej zawierającej przekątną 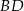 tego rombu.
tego rombu.
A) 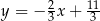 B)
B) 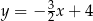 C)
C) 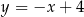 D)
D) 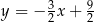
Jeśli  jest kątem ostrym i
jest kątem ostrym i 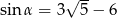 , to
, to 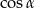 jest równy
jest równy
A) 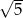 B)
B) 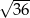 C)
C) 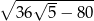 D)
D) 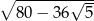
Jeśli  jest kątem ostrym i
jest kątem ostrym i 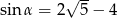 , to
, to 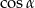 jest równy
jest równy
A) 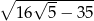 B)
B) 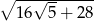 C)
C) 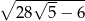 D)
D) 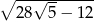
Jeśli  jest kątem ostrym i
jest kątem ostrym i 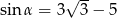 , to
, to 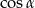 jest równy
jest równy
A) 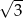 B)
B) 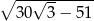 C)
C) 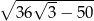 D)
D)