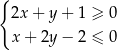Prosta 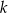 ma równanie
ma równanie 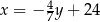 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 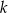 jest równy
jest równy
A)  B)
B) 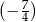 C)
C) 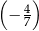 D)
D) 
/Szkoła średnia/Zadania testowe
Firma 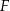 zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy 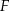 , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
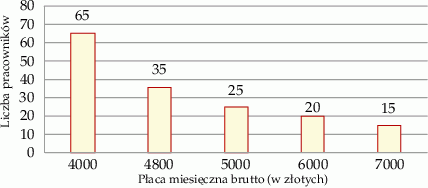
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Mediana miesięcznej płacy pracowników firmy 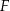 jest równa 4800 zł. jest równa 4800 zł. | P | F |
| Ponad 78% pracowników tej firmy zarabia nie więcej niż 5000 zł brutto. | P | F |
Trójkąt 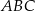 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 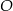 . Miara kąta
. Miara kąta 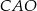 jest równa
jest równa 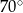 (zobacz rysunek).
(zobacz rysunek).
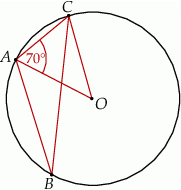
Wtedy miara kąta 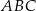 jest równa
jest równa
A) 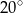 B)
B) 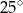 C)
C) 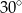 D)
D) 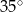
Wyrażenie 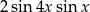 jest równe
jest równe
A) 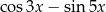 B)
B) 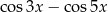 C)
C) 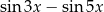 D)
D) 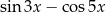
Wyrażenie 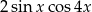 jest równe
jest równe
A) 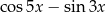 B)
B) 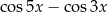 C)
C) 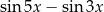 D)
D) 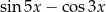
W pudełku znajdują się tylko kule białe, kule czerwone i kule zielone. Prawdopodobieństwo wylosowania z pudełka kuli zielonej jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czerwonej i dwa razy mniejsze niż wylosowanie kuli białej. Prawdopodobieństwo wylosowania z pudełka kuli zielonej jest równe
A) 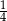 B)
B) 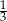 C)
C)  D)
D) 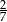
W pudełku znajdują się tylko kule białe, kule czerwone i kule zielone. Prawdopodobieństwo wylosowania z pudełka kuli czerwonej jest dwa razy większe niż prawdopodobieństwo wylosowania kuli białej i dwa razy mniejsze niż wylosowanie kuli zielonej. Prawdopodobieństwo wylosowania z pudełka kuli białej jest równe
A) 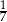 B)
B) 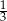 C)
C)  D)
D) 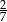
Słoń waży 5 ton, a waga mrówki jest równa 0,5 grama. Ile razy słoń jest cięższy od mrówki?
A) 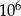 B)
B) 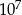 C) 10 D)
C) 10 D) 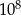
Wieża Eiffla ma wysokość 300 m, a pantofelek ma długość 0,3 mm. Ile razy wieża Eiffla jest wyższa od długości pantofelka?
A) 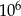 B)
B) 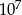 C) 1000 D)
C) 1000 D) 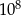
W pewnym zoo mieszkają słoń afrykański o masie 6 ton oraz góralek skalny o masie 3 kg. Masa słonia afrykańskiego jest większa niż masa góralka skalnego
A) 20 razy. B) 200 razy. C) 2 000 razy. D) 20 000 razy.
Dany jest nieskończony rosnący ciąg arytmetyczny 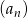 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 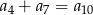 B)
B) 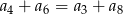 C)
C) 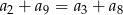 D)
D) 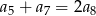
Dany jest nieskończony rosnący ciąg arytmetyczny 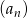 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 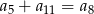 B)
B) 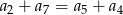 C)
C) 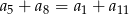 D)
D) 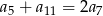
Dany jest nieskończony rosnący ciąg arytmetyczny 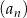 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 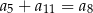 B)
B) 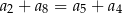 C)
C) 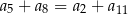 D)
D) 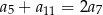
Wielomiany 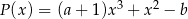 i
i 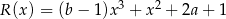 są równe. Zatem liczba
są równe. Zatem liczba 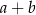
A) należy do zbioru 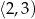 B) jest większa od 3
B) jest większa od 3
C) należy do zbioru 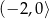 D) jest mniejsza od -2
D) jest mniejsza od -2
Dana jest funkcja
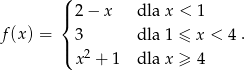
Wówczas
A) 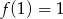 B)
B) 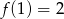 C)
C) 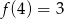 D)
D) 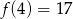
Jeśli funkcja 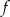 określona jest wzorem
określona jest wzorem
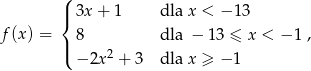
to
A) 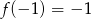 B)
B) 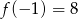 C)
C) 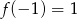 D)
D) 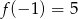
Cenę telewizora obniżono o 15%, a następnie o 2%. Klient kupił telewizor po obniżonej cenie i dzięki temu zapłacił o 501 zł mniej, niż zapłaciłby przed obniżkami. Przed obniżkami ten telewizor kosztował
A) 2947 zł B) 4000 zł C) 3000 zł D) 2840 zł
Cenę laptopa podwyższono o 12%, a następnie o 19%. W wyniku tych podwyżek cena laptopa wzrosła o 832 zł. Przed podwyżkami ten laptop kosztował
A) 3332 zł B) 2500 zł C) 3000 zł D) 2375 zł
Iloczyn dwóch wielomianów, z których każdy jest stopnia piątego, może być wielomianem stopnia
A) drugiego B) szóstego C) dziesiątego D) dwudziestego piątego
Punkty 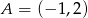 i
i 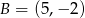 są dwoma sąsiednimi wierzchołkami rombu
są dwoma sąsiednimi wierzchołkami rombu 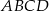 . Obwód tego rombu jest równy
. Obwód tego rombu jest równy
A) 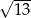 B) 13 C) 676 D)
B) 13 C) 676 D) 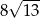
Punkty 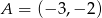 i
i 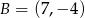 są dwoma sąsiednimi wierzchołkami rombu
są dwoma sąsiednimi wierzchołkami rombu 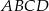 . Obwód tego rombu jest równy
. Obwód tego rombu jest równy
A) 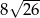 B)
B) 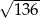 C)
C) 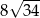 D)
D) 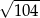
Na rysunku przedstawiono fragmenty dwóch prostych na płaszczyźnie oraz zaznaczono kilka punktów o współrzędnych całkowitych, przez które przechodzą te proste.
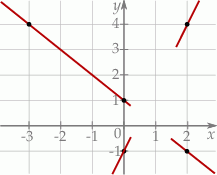
Jeżeli 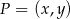 jest punktem wspólnym prostych, których fragmenty przedstawiono na rysunku, to
jest punktem wspólnym prostych, których fragmenty przedstawiono na rysunku, to
A) 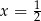 B)
B) 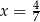 C)
C) 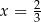 D)
D) 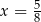
Jeśli średnica podstawy stożka jest równa 12, a wysokość stożka 8, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 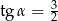 B)
B) 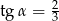 C)
C) 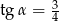 D)
D) 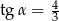
Jeśli średnica podstawy stożka jest równa 18, a wysokość stożka 12, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 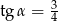 B)
B) 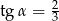 C)
C) 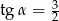 D)
D) 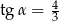
Jeśli średnica podstawy stożka jest równa 16, a wysokość stożka 6, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 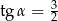 B)
B) 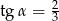 C)
C) 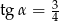 D)
D) 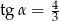
Miejscami zerowymi funkcji kwadratowej 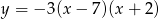 są
są
A) 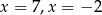 B)
B) 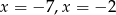 C)
C) 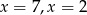 D)
D) 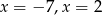
Miejscami zerowymi funkcji kwadratowej 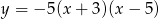 są
są
A) 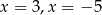 B)
B) 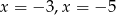 C)
C) 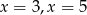 D)
D) 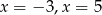
Reszta z dzielenia wielomianu 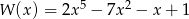 przez dwumian
przez dwumian 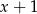 jest równa
jest równa
A) 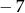 B) 7 C) 5 D) 11
B) 7 C) 5 D) 11
Reszta z dzielenia wielomianu 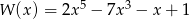 przez dwumian
przez dwumian 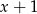 jest równa
jest równa
A) 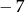 B) 7 C) 5 D) 11
B) 7 C) 5 D) 11
Reszta z dzielenia wielomianu 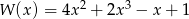 przez dwumian
przez dwumian 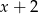 jest równa
jest równa
A) 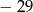 B) 3 C)
B) 3 C) 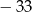 D) 35
D) 35
Reszta z dzielenia wielomianu 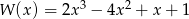 przez dwumian
przez dwumian 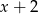 jest równa
jest równa
A) 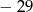 B) 3 C)
B) 3 C) 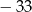 D)
D) 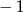
Reszta z dzielenia wielomianu 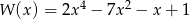 przez dwumian
przez dwumian 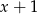 jest równa
jest równa
A) 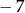 B) 7 C)
B) 7 C) 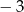 D) 11
D) 11
Reszta z dzielenia wielomianu 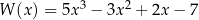 przez dwumian
przez dwumian 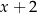 jest równa
jest równa
A) 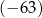 B)
B) 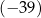 C) 25 D) 41
C) 25 D) 41
Reszta z dzielenia wielomianu 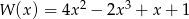 przez dwumian
przez dwumian 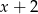 jest równa
jest równa
A) 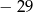 B) 3 C)
B) 3 C) 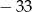 D) 31
D) 31
Reszta z dzielenia wielomianu 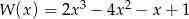 przez dwumian
przez dwumian 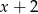 jest równa
jest równa
A) 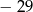 B) 3 C)
B) 3 C) 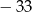 D)
D) 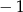
Reszta z dzielenia wielomianu 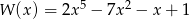 przez dwumian
przez dwumian 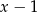 jest równa
jest równa
A) 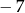 B) 7 C)
B) 7 C) 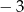 D)
D) 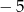
Reszta z dzielenia wielomianu 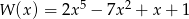 przez dwumian
przez dwumian 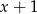 jest równa
jest równa
A) 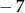 B)
B) 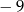 C) 5 D) 11
C) 5 D) 11
W trójkącie prostokątnym 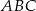 , w którym
, w którym 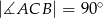 , na boku
, na boku 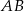 wybrano punkt
wybrano punkt 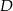 taki, że
taki, że 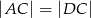 (zobacz rysunek).
(zobacz rysunek).
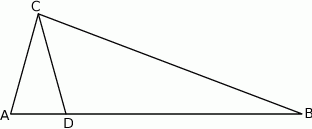
Wynika stąd, że różnica miar kątów 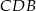 i
i 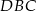 jest równa
jest równa
A) 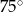 B)
B) 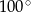 C)
C) 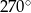 D)
D) 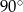
Jeżeli 75% liczby  jest równe 177 i 59% liczby
jest równe 177 i 59% liczby 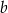 jest równe 177, to
jest równe 177, to
A) 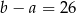 B)
B) 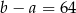 C)
C) 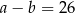 D)
D) 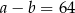
Jeżeli 59% liczby 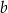 jest równe 177 i
jest równe 177 i 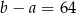 , to 75% liczby
, to 75% liczby  jest równe
jest równe
A) 236 B) 300 C) 225 D) 177
Jeżeli 37% liczby  jest równe 148 i 25% liczby
jest równe 148 i 25% liczby 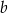 jest równe 148, to
jest równe 148, to
A) 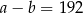 B)
B) 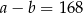 C)
C) 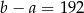 D)
D) 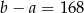
Liczby 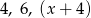 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas liczba
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas liczba  jest równa:
jest równa:
A) 9 B) 10 C) 13 D) 5
Trzywyrazowy ciąg 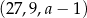 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 3 B) 0 C) 4 D) 2
Dany jest trzywyrazowy ciąg geometryczny 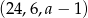 . Stąd wynika, że
. Stąd wynika, że
A) 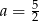 B)
B) 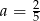 C)
C) 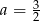 D)
D) 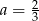
Dany jest ciąg liczbowy 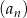 , w którym
, w którym 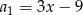 ,
, 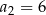 ,
, 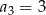 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem geometrycznym?
dany ciąg jest ciągiem geometrycznym?
A) 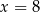 B)
B) 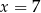 C)
C) 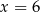 D)
D) 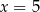
Trzywyrazowy ciąg 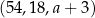 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 3 B) 6 C) 4 D) 2
Ciąg 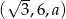 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 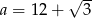 B)
B) 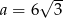 C)
C) 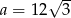 D)
D) 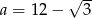
Liczby 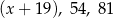 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas pierwszy wyraz tego ciągu jest równy:
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas pierwszy wyraz tego ciągu jest równy:
A) 62 B) 36 C) 35 D) 17
Liczby 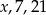 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 1 B)  C)
C) 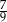 D)
D) 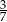
Liczby 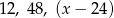 są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas trzeci wyraz tego ciągu jest równy:
są trzema początkowymi wyrazami ciągu geometrycznego. Wówczas trzeci wyraz tego ciągu jest równy:
A) 192 B) 216 C) 60 D) 24
Ciąg 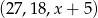 jest geometryczny. Wtedy
jest geometryczny. Wtedy
A) 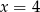 B)
B) 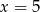 C)
C) 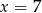 D)
D) 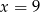
Liczby: 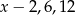 , w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
, w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 0 B) 2 C) 3 D) 5
Liczby 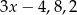 w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy
w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy
A) 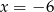 B)
B) 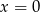 C)
C) 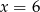 D)
D) 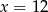
Trzywyrazowy ciąg 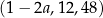 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 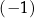 B) 3 C) 4 D) 12,5
B) 3 C) 4 D) 12,5
Ciąg 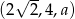 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 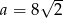 B)
B) 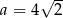 C)
C) 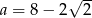 D)
D) 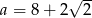
Trzywyrazowy ciąg 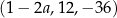 jest geometryczny. Liczba
jest geometryczny. Liczba  jest równa
jest równa
A) 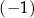 B) 5 C) 4 D) 2,5
B) 5 C) 4 D) 2,5
Ciąg 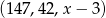 jest geometryczny. Wtedy
jest geometryczny. Wtedy
A) 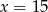 B)
B) 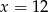 C)
C) 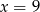 D)
D) 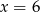
Liczby 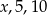 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa
A) 2,5 B) 5 C) 10 D) 0
Liczby 9,-3 i 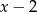 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  jest równa
jest równa
A) 1 B) -1,5 C) 5 D) 3
Liczby -8,4 i 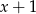 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba
(w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wówczas liczba  jest równa
jest równa
A) -3 B) -1,5 C) 1 D) 15
Trójwyrazowy ciąg 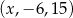 jest ciągiem geometrycznym. Wtedy
jest ciągiem geometrycznym. Wtedy
A) 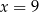 B)
B) 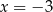 C)
C) 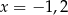 D)
D) 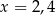
Na rysunku zaznaczono zbiór punktów płaszczyzny spełniających układ nierówności:
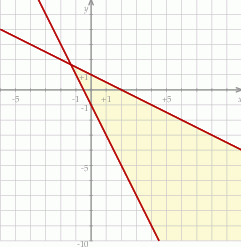
A) 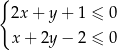 B)
B) 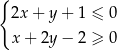
C) 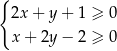 D)
D)