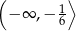Ze zbioru liczb 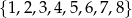 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 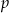 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 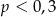 B)
B) 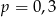 C)
C) 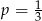 D)
D) 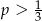
/Szkoła średnia/Zadania testowe
Ze zbioru liczb 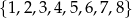 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 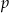 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A) 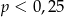 B)
B) 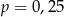 C)
C) 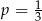 D)
D) 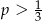
Ze zbioru liczb 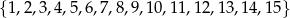 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 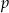 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 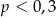 B)
B) 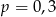 C)
C) 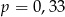 D)
D) 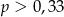
Ze zbioru liczb 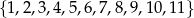 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 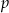 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 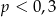 B)
B) 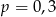 C)
C) 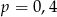 D)
D) 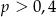
Ze zbioru 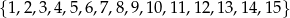 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 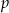 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
A) 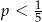 B)
B) 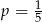 C)
C) 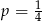 D)
D) 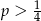
Ciągiem geometrycznym o ilorazie 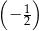 jest ciąg określony wzorem
jest ciąg określony wzorem
A) 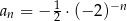 B)
B) 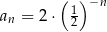 C)
C) 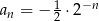 D)
D) 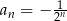
Wyrażenie 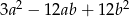 może być przekształcone do postaci
może być przekształcone do postaci
A) 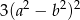 B)
B) 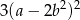 C)
C) 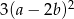 D)
D) 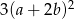
Wyrażenie 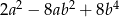 może być przekształcone do postaci
może być przekształcone do postaci
A) 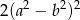 B)
B) 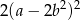 C)
C) 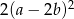 D)
D) 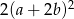
Liczba 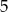 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 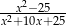 B)
B) 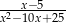 C)
C) 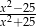 D)
D) 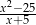
Liczba 4 nie należy do dziedziny wyrażenia
A) 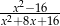 B)
B) 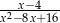 C)
C) 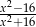 D)
D) 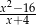
Liczba -5 nie należy do dziedziny wyrażenia
A) 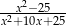 B)
B) 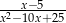 C)
C) 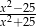 D)
D) 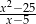
Liczba 3 nie należy do dziedziny wyrażenia
A) 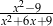 B)
B) 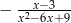 C)
C) 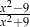 D)
D) 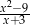
Dla 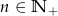 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A)  B)
B) 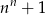 C)
C) 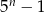 D)
D) 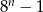
Dla 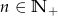 zawsze parzysta jest liczba
zawsze parzysta jest liczba
A) 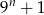 B)
B) 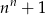 C)
C) 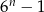 D)
D) 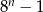
Dla 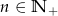 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
A) 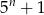 B)
B) 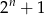 C)
C) 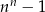 D)
D) 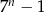
Średnia arytmetyczna pięciu liczb: 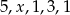 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 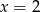 B)
B) 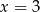 C)
C) 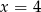 D)
D) 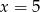
Średnia arytmetyczna zestawu danych: 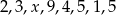 wynosi 4,5. Wynika z tego, że:
wynosi 4,5. Wynika z tego, że:
A) 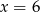 B)
B) 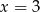 C)
C) 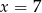 D)
D) 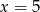
Średnia arytmetyczna pięciu liczb: 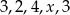 jest równa 3,2. Wtedy
jest równa 3,2. Wtedy
A) 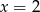 B)
B) 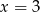 C)
C) 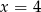 D)
D) 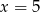
Średnia arytmetyczna dziesięciu liczb 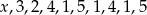 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 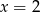 B)
B) 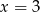 C)
C) 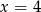 D)
D) 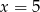
Średnia arytmetyczna siedmiu liczb: 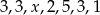 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 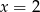 B)
B) 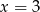 C)
C) 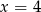 D)
D) 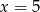
Średnia arytmetyczna pięciu liczb: 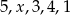 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 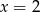 B)
B) 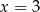 C)
C) 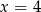 D)
D) 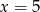
Średnia arytmetyczna ośmiu liczb: 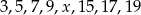 jest równa 11. Wtedy
jest równa 11. Wtedy
A) 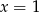 B)
B) 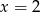 C)
C) 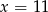 D)
D) 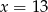
Średnia arytmetyczna pięciu liczb: 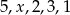 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 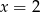 B)
B) 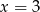 C)
C) 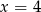 D)
D) 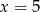
Średnia arytmetyczna sześciu liczb: 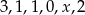 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Średnia arytmetyczna zestawu danych: 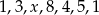 wynosi 4. Wynika z tego, że:
wynosi 4. Wynika z tego, że:
A) 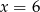 B)
B) 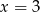 C)
C) 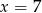 D)
D) 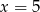
Dla jakiej wartości liczbowej  średnia arytmetyczna liczb:
średnia arytmetyczna liczb: 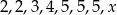 jest równa 4?
jest równa 4?
A) 6 B) 5 C) 4 D) 3
Średnia arytmetyczna zestawu sześciu liczb: 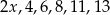 , jest równa 5. Wynika stąd, że
, jest równa 5. Wynika stąd, że
A) 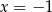 B)
B) 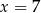 C)
C) 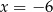 D)
D) 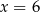
Średnia arytmetyczna liczb 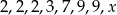 jest równa 4,5. Liczba
jest równa 4,5. Liczba  jest równa
jest równa
A) 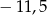 B) 1 C) 1,5 D) 2
B) 1 C) 1,5 D) 2
Średnia arytmetyczna dziesięciu liczb 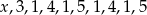 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 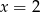 B)
B) 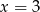 C)
C) 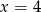 D)
D) 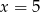
Średnia arytmetyczna liczb: 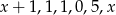 jest równa
jest równa  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A)  B) 2 C)
B) 2 C)  D)
D) 
Średnia arytmetyczna zestawu danych: 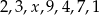 wynosi
wynosi 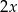 . Wynika z tego, że:
. Wynika z tego, że:
A) 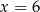 B)
B) 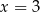 C)
C) 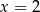 D)
D) 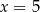
Liczba miejsc zerowych funkcji 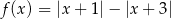 , gdzie
, gdzie 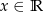 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Funkcja 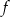 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 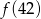 ,
, 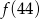 ,
, 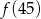 ,
, 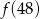 największa to
największa to
A) 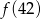 B)
B) 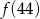 C)
C) 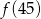 D)
D) 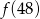
Funkcja 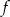 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 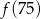 ,
, 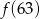 ,
, 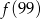 ,
, 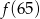 największa to
największa to
A) 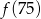 B)
B) 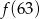 C)
C) 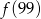 D)
D) 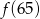
W ciągu arytmetycznym 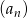 wyraz
wyraz 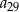 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 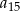 oraz
oraz 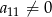 . Wtedy iloraz
. Wtedy iloraz 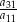 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
W ciągu arytmetycznym 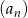 wyraz
wyraz 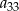 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 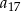 oraz
oraz 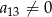 . Wtedy iloraz
. Wtedy iloraz 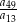 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Jeżeli 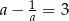 to liczba
to liczba 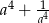 jest równa
jest równa
A) 121 B) 119 C) 123 D) 81
Jeżeli 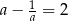 , to liczba
, to liczba 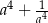 jest równa
jest równa
A) 36 B) 34 C) 6 D) 16
Jeżeli 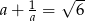 to liczba
to liczba 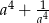 jest równa
jest równa
A) 16 B) 6 C) 14 D) 36
W pewnym zakładzie pracy w wyniku dwóch podwyżek zwiększono pensje pracowników o 26%. W ramach pierwszej z tych podwyżek płace zwiększono o 20%. O ile procent zwiększono płace w ramach drugiej podwyżki?
A) o 12% B) o 6% C) o 5% D) o 10%
W wyniku dwóch obniżek cenę komputera obniżono o 40%. Druga z tych obniżek była obniżką o 25%. O ile procent obniżono cenę komputera przy pierwszej obniżce?
A) o 15% B) o 65% C) o 20% D) o 30%
W wyniku dwóch obniżek cenę spodni obniżono o 52%. W ramach pierwszej z tych obniżek cenę zmniejszono o 20%. O ile procent zmniejszono cenę w ramach drugiej obniżki?
A) o 60% B) o 40% C) o 20% D) o 50%
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy 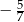 . Wskaż równanie prostej
. Wskaż równanie prostej 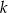 .
.
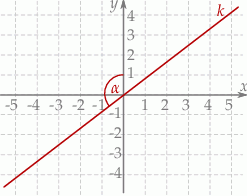
A) 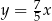 B)
B) 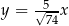 C)
C) 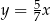 D)
D) 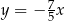
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa 90. Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A) 300 B) 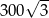 C)
C) 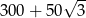 D)
D) 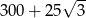
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa 72. Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A) 192 B) 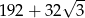 C)
C) 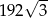 D)
D) 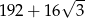
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 5 dają resztę 3. Dziesiąty wyraz tego ciągu jest równy
A) 43 B) 53 C) 58 D) 68
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 4 dają resztę 3. Dwunasty wyraz tego ciągu jest równy
A) 51 B) 55 C) 59 D) 63
Wyrazami ciągu są liczby naturalne dwucyfrowe, które przy dzieleniu przez 7 dają resztę 4. Dziewiąty wyraz tego ciągu jest równy
A) 53 B) 74 C) 60 D) 67
Pole trójkąta równobocznego wpisanego w okrąg o promieniu 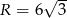 jest równe
jest równe
A) 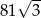 B)
B) 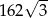 C)
C) 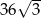 D)
D) 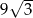
Pole trójkąta równobocznego wpisanego w okrąg o promieniu 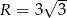 jest równe
jest równe
A) 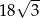 B)
B) 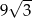 C)
C) 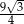 D)
D) 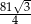
Pole trójkąta równobocznego wpisanego w okrąg o promieniu 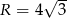 jest równe
jest równe
A) 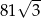 B)
B) 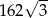 C)
C) 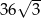 D)
D) 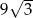
Na rysunku przedstawiono wykresy trzech parami przecinających się prostych
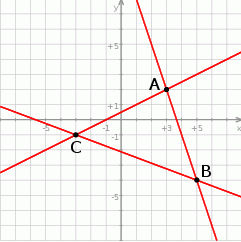
Te proste to
A) 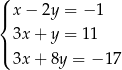 B)
B) 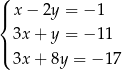 C)
C) 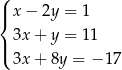 D)
D) 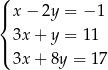
Pole wycinka koła (zacieniowana część na rysunku) jest równe
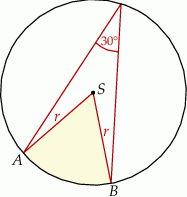
A) 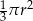 B)
B) 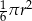 C)
C) 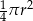 D)
D) 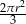
Pole wycinka koła (zacieniowana część na rysunku) jest równe
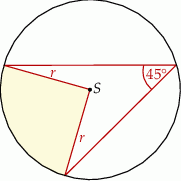
A) 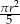 B)
B) 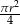 C)
C) 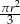 D)
D) 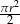
Do wykresu funkcji 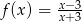 należy punkt
należy punkt
A) 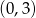 B)
B) 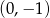 C)
C) 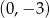 D)
D) 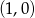
Do wykresu funkcji 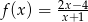 należy punkt
należy punkt
A) 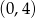 B)
B) 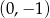 C)
C) 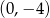 D)
D) 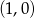
Dane są dwa okręgi o środkach 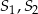 i promieniach odpowiednio równych
i promieniach odpowiednio równych 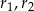 . Jeśli
. Jeśli 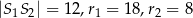 , to okręgi
, to okręgi
A) nie mają punktów wspólnych B) są styczne wewnętrznie
C) mają dwa punkty wspólne D) są styczne zewnętrznie
Jakie jest wzajemne położenie okręgów 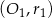 i
i 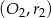 jeżeli wiadomo, że:
jeżeli wiadomo, że: 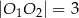 ,
, 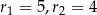
A) rozłączne zewnętrznie B) współśrodkowe
C) rozłączne wewnętrznie D) przecinające się
Dane są dwa okręgi o środkach 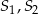 i promieniach odpowiednio równych
i promieniach odpowiednio równych 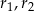 . Jeśli
. Jeśli 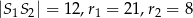 , to okręgi
, to okręgi
A) nie mają punktów wspólnych B) są styczne wewnętrznie
C) mają dwa punkty wspólne D) są styczne zewnętrznie
Dane są dwa okręgi o środkach 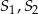 i promieniach odpowiednio równych
i promieniach odpowiednio równych 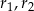 . Jeśli
. Jeśli 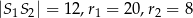 , to okręgi
, to okręgi
A) nie mają punktów wspólnych B) są styczne wewnętrznie
C) mają dwa punkty wspólne D) są styczne zewnętrznie
Rozwiązaniem nierówności 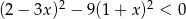 jest zbiór
jest zbiór
A) 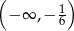 B)
B) 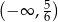 C)
C) 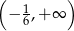 D)
D) 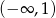
Rozwiązaniem nierówności 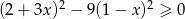 jest zbiór
jest zbiór
A) 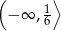 B)
B) 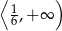 C)
C) 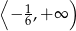 D)
D)