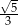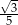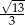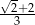Przekątna podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości ostrosłupa. Ostrosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i środek jednej z krawędzi bocznych (patrz rysunek).
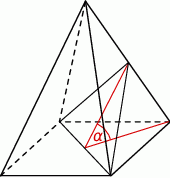
Płaszczyzna przekroju tworzy z podstawą ostrosłupa kąt  o mierze
o mierze
A) 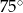 B)
B) 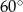 C)
C) 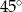 D)
D) 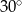

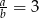 , to wartość wyrażenia
, to wartość wyrażenia 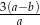 jest równa
jest równa 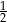

 i
i 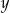 spełniają warunek
spełniają warunek 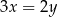 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 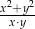 jest równa
jest równa 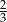
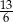
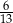

 i
i 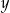 spełniają warunek
spełniają warunek 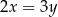 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 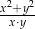 jest równa
jest równa 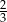
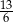
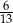

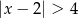
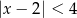
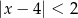
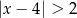
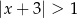
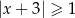
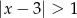
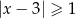
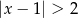
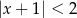
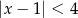
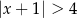
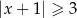
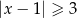
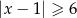
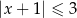
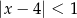
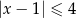
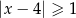
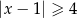
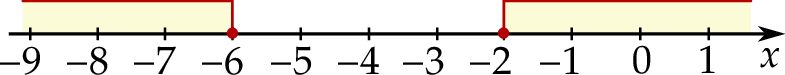
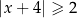
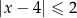
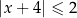
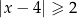
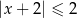
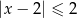
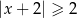
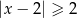
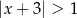
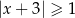
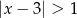
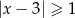
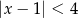
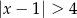
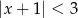
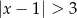
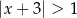
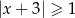
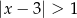
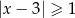
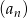 jest określony wzorem
jest określony wzorem 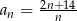 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa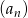 jest określony wzorem
jest określony wzorem 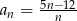 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa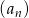 jest określony wzorem
jest określony wzorem 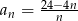 dla
dla 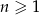 . Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
. Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa 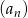 jest określony wzorem
jest określony wzorem 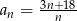 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa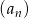 jest określony wzorem
jest określony wzorem 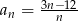 dla
dla 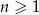 . Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa
. Liczba wszystkich całkowitych nieujemnych wyrazów tego ciągu jest równa 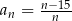 . Liczba całkowitych wyrazów tego ciągu jest równa
. Liczba całkowitych wyrazów tego ciągu jest równa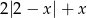 dla
dla 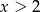 ma wartość
ma wartość 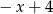
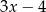
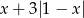 dla
dla 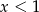 ma wartość
ma wartość 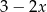
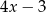

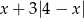 dla
dla 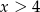 ma wartość
ma wartość 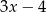
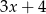
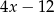
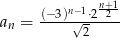 , dla
, dla 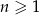 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy 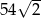
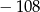
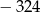
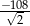
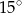 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe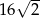
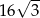
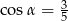 , to wartość wyrażenia
, to wartość wyrażenia 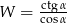 jest równa
jest równa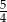
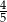
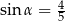 , to wartość wyrażenia
, to wartość wyrażenia 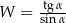 jest równa
jest równa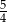
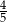
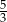

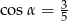 , to wartość wyrażenia
, to wartość wyrażenia 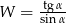 jest równa
jest równa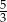
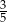
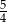

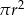 powiększono 2 razy. Objętość tak zmienionej kuli jest równa
powiększono 2 razy. Objętość tak zmienionej kuli jest równa 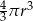
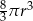
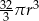
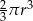
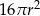 zmniejszono 2 razy. Objętość tak zmienionej kuli jest równa
zmniejszono 2 razy. Objętość tak zmienionej kuli jest równa 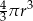
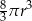
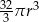
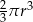
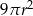 powiększono 2 razy. Objętość tak zmienionej kuli jest równa
powiększono 2 razy. Objętość tak zmienionej kuli jest równa 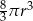
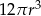
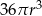
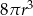
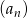 , w którym
, w którym 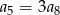 . Wtedy
. Wtedy 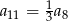
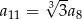
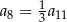
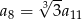
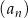 , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej 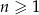 , są dodatnie i
, są dodatnie i 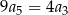 . Wtedy iloraz tego ciągu jest równy
. Wtedy iloraz tego ciągu jest równy 

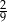
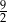
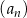 , w którym
, w którym 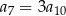 . Wtedy
. Wtedy 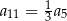
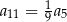
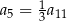
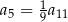
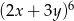 współczynnik przy iloczynie
współczynnik przy iloczynie 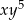 jest równy
jest równy 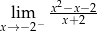
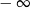
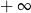
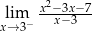
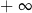
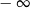
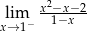
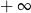
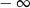
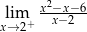
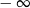
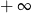
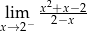
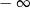
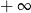
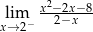
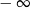
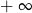
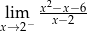
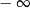
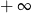
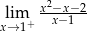
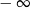
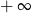
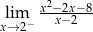
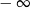
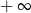
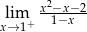
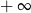
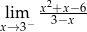
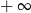
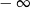
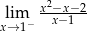
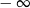
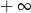
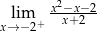
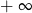
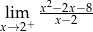
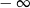

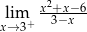
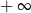
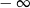
 mają długości 12 cm, 15 cm, 18 cm. Trójkąt
mają długości 12 cm, 15 cm, 18 cm. Trójkąt 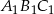 jest podobny do trójkąta
jest podobny do trójkąta 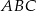 . Najdłuższy bok trójkąta
. Najdłuższy bok trójkąta 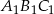 ma długość 6 cm. Obwód trójkąta
ma długość 6 cm. Obwód trójkąta 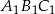 jest równy
jest równy 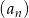 jest określony wzorem
jest określony wzorem 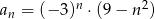 dla
dla 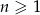 . Wynika stąd, że
. Wynika stąd, że 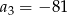
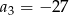
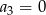
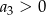
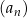 jest określony wzorem
jest określony wzorem 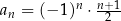 dla każdej liczby naturalnej
dla każdej liczby naturalnej 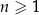 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy 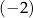
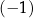
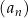 jest określony wzorem
jest określony wzorem 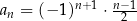 dla każdej liczby naturalnej
dla każdej liczby naturalnej 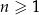 . Piąty wyraz tego ciągu jest równy
. Piąty wyraz tego ciągu jest równy 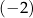
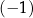
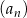 jest określony wzorem
jest określony wzorem 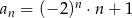 dla każdej liczby naturalnej
dla każdej liczby naturalnej 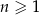 . Wtedy trzeci wyraz tego ciągu jest równy
. Wtedy trzeci wyraz tego ciągu jest równy 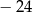
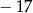
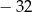
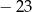
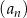 jest określony wzorem
jest określony wzorem 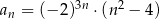 dla
dla 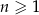 . Wówczas
. Wówczas 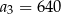
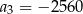
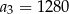
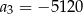
 jest określony wzorem
jest określony wzorem 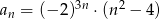 dla
dla 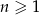 . Wówczas
. Wówczas 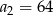
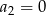
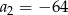
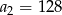
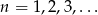 ciąg
ciąg 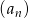 jest określony wzorem
jest określony wzorem 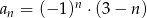 . Wtedy
. Wtedy 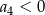
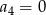
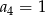
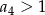
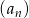 jest określony wzorem
jest określony wzorem 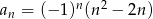 dla
dla 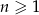 . Wtedy
. Wtedy 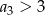
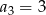
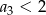
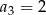
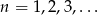 ciąg
ciąg 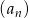 jest określony wzorem
jest określony wzorem 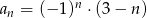 . Wtedy
. Wtedy 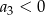
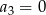
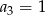
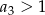
 jest określony wzorem
jest określony wzorem 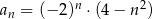 , dla
, dla 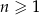 . Wtedy
. Wtedy 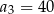
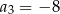
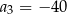
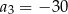
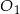 i
i 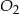 mają takie same wysokości. Długość krawędzi podstawy ostrosłupa
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa 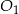 jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa
jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa 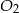 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 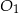 do objętości ostrosłupa
do objętości ostrosłupa 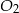 jest równy
jest równy 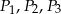 . Wówczas
. Wówczas 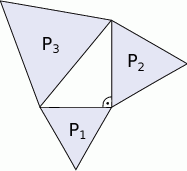
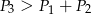
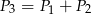
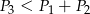
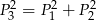
 jest ostry oraz
jest ostry oraz 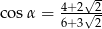 . Wtedy
. Wtedy 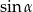 jest równy
jest równy