Wielomian 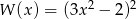 jest równy wielomianowi
jest równy wielomianowi
A) 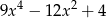 B)
B) 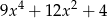 C)
C) 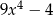 D)
D) 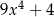
/Szkoła średnia/Zadania testowe
Wielomian 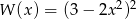 jest równy wielomianowi
jest równy wielomianowi
A) 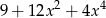 B)
B) 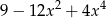 C)
C) 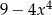 D)
D) 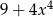
Równanie 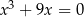
A) nie ma pierwiastków B) ma jeden pierwiastek
C) ma dwa pierwiastki D) ma trzy pierwiastki
Równanie 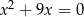
A) nie ma pierwiastków B) ma jeden pierwiastek
C) ma dwa pierwiastki D) ma trzy pierwiastki
Równanie 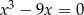
A) nie ma pierwiastków B) ma jeden pierwiastek
C) ma dwa pierwiastki D) ma trzy pierwiastki
Ciąg 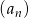 jest określony wzorem
jest określony wzorem 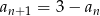 dla każdej liczby naturalnej
dla każdej liczby naturalnej 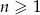 . Suma pięćdziesięciu początkowych wyrazów tego ciągu jest równa
. Suma pięćdziesięciu początkowych wyrazów tego ciągu jest równa
A) 150 B) 75 C) 50 D) 100
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 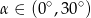 B)
B) 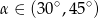 C)
C) 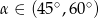 D)
D) 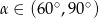
Wiadomo, że tangens kąta ostrego  jest równy
jest równy  . Wobec tego:
. Wobec tego:
A) 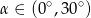 B)
B) 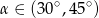 C)
C) 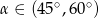 D)
D) 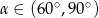
Wiadomo, że tangens kąta ostrego  jest równy
jest równy 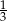 . Wobec tego:
. Wobec tego:
A) 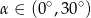 B)
B) 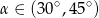 C)
C) 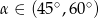 D)
D) 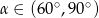
Punkty 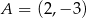 i
i 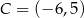 są wierzchołkami rombu
są wierzchołkami rombu 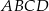 . Środkiem okręgu wpisanego w romb jest punkt
. Środkiem okręgu wpisanego w romb jest punkt
A) 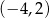 B)
B) 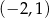 C)
C) 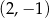 D)
D) 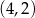
Punkty 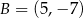 i
i 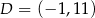 są wierzchołkami rombu
są wierzchołkami rombu 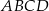 . Środkiem okręgu wpisanego w romb jest punkt
. Środkiem okręgu wpisanego w romb jest punkt
A) 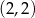 B)
B) 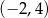 C)
C) 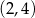 D)
D) 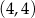
Punkty 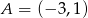 i
i 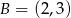 są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
A) 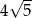 B)
B) 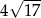 C)
C) 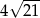 D)
D) 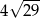
Punkty 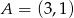 i
i 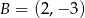 są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
są kolejnymi wierzchołkami kwadratu. Obwód tego kwadratu jest równy
A) 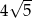 B)
B) 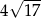 C)
C) 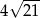 D)
D) 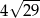
Pewnego dnia w klasie liczącej 11 dziewcząt i 15 chłopców nieobecny był jeden chłopiec i jedna dziewczynka. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 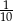 B)
B) 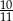 C)
C) 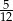 D)
D) 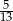
Pewnego dnia w klasie liczącej 16 dziewcząt i 12 chłopców nieobecnych było dwóch chłopców i trzy dziewczynki. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 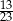 B)
B) 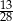 C)
C) 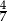 D)
D) 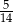
Dane są dwa okręgi o promieniach 12 i 17. Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa
A) 5 B) 12 C) 17 D) 29
Dane są dwa okręgi o promieniach 10 i 15. Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa
A) 2,5 B) 5 C) 10 D) 12,5
Dane są dwa okręgi o promieniach 12 i 17. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 5 B) 12 C) 17 D) 29
Dane są dwa okręgi o promieniach 10 i 18. Większy okrąg przechodzi przez środek mniejszego okręgu. Odległość między środkami tych okręgów jest równa
A) 18 B) 8 C) 10 D) 28
Wskaż liczbę, której 4% jest równe 8.
A) 3,2 B) 32 C) 100 D) 200
Jeżeli 8,5% liczby  jest równe 163,2, to liczba
jest równe 163,2, to liczba  jest równa
jest równa
A) 19200 B) 1920 C) 1387,2 D) 13872
4,5% liczby  jest równe 48,6. Liczba
jest równe 48,6. Liczba  jest równa
jest równa
A) 1080 B) 108 C) 48,6 D) 4,86
Wskaż liczbę, której 0,4% jest równe 12.
A) 0,048 B) 0,48 C) 30 D) 3000
Liczba 42 jest równa 0,6% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 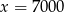 B)
B) 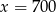 C)
C) 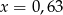 D)
D) 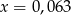
Jeżeli 35% pewnej liczby  jest równe 140 to
jest równe 140 to
A) 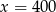 B)
B) 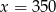 C)
C) 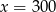 D)
D) 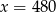
Liczba 78 stanowi 150% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 60 B) 52 C) 48 D) 39
Liczba 609 stanowi 140% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 420 B) 435 C) 468 D) 406
Wskaż liczbę, której 6% jest równe 6.
A) 0,36 B) 3,6 C) 10 D) 100
Dla każdej liczby rzeczywistej  różnej od
różnej od 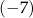 i 7 wartość wyrażenia
i 7 wartość wyrażenia
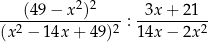
jest równa wartości wyrażenia
A) 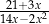 B)
B) 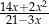 C)
C) 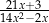 D)
D) 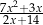
Kąty wewnętrzne przy wierzchołkach 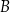 i
i 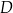 trapezu
trapezu 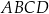 są równe odpowiednio
są równe odpowiednio 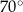 i
i 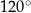 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 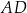 i
i 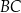 przecinają się pod kątem
przecinają się pod kątem
A) 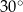 B)
B) 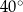 C)
C) 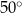 D)
D) 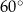
Kąty wewnętrzne przy wierzchołkach 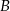 i
i 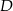 trapezu
trapezu 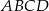 są równe odpowiednio
są równe odpowiednio 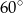 i
i 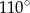 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 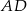 i
i 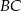 przecinają się pod kątem
przecinają się pod kątem
A) 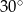 B)
B) 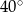 C)
C) 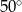 D)
D) 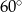
Wielomian 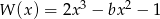 jest podzielny przez dwumian
jest podzielny przez dwumian 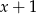 . Wynika stąd, że
. Wynika stąd, że
A) 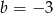 B)
B) 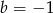 C)
C) 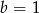 D)
D) 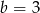
Wielomian 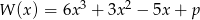 jest podzielny przez dwumian
jest podzielny przez dwumian 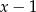 dla
dla 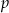 równego
równego
A) 4 B) 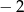 C) 2 D)
C) 2 D) 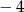
Wielomian 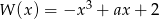 jest podzielny przez dwumian
jest podzielny przez dwumian 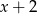 . Wynika stąd, że
. Wynika stąd, że
A) 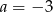 B)
B) 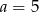 C)
C) 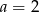 D)
D) 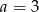
Wielomian 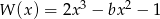 jest podzielny przez dwumian
jest podzielny przez dwumian 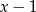 . Wynika stąd, że
. Wynika stąd, że
A) 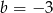 B)
B) 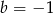 C)
C) 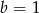 D)
D) 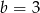
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 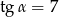 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 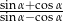 jest równa
jest równa
A) 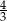 B)
B)  C)
C)  D)
D) 
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 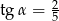 , to wartość wyrażenia
, to wartość wyrażenia 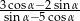 jest równa
jest równa
A) 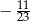 B)
B) 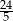 C)
C) 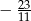 D)
D) 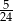
Jeżeli kąt  jest ostry i
jest ostry i 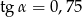 , to wartość wyrażenia
, to wartość wyrażenia 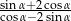 jest równa
jest równa
A) 11 B) 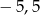 C)
C) 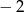 D)
D) 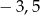
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 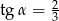 , to wartość wyrażenia
, to wartość wyrażenia 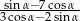 jest równa
jest równa
A) 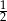 B)
B) 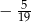 C)
C) 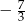 D)
D) 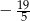
Jeżeli 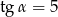 , to wartość wyrażenia
, to wartość wyrażenia 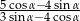 jest równa
jest równa
A) 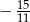 B)
B) 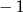 C)
C) 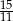 D)
D) 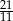
W okręgu o środku w punkcie 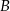 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 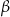 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 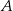 i
i 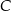 leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta
leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta 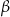 znajduje się w punkcie
znajduje się w punkcie 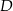 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 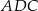 jest równoboczny B)
jest równoboczny B) 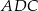 jest prostokątny
jest prostokątny
C) 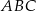 jest równoboczny D)
jest równoboczny D) 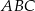 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 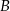 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 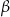 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 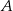 i
i 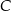 leżące na okręgu. Suma miar tych kątów jest równa
leżące na okręgu. Suma miar tych kątów jest równa 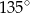 . Wierzchołek kąta
. Wierzchołek kąta 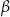 znajduje się w punkcie
znajduje się w punkcie 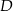 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 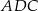 jest równoboczny B)
jest równoboczny B) 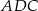 jest prostokątny
jest prostokątny
C) 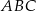 jest równoboczny D)
jest równoboczny D) 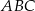 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 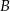 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 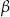 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 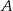 i
i 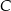 leżące na okręgu. Różnica miar tych kątów jest równa
leżące na okręgu. Różnica miar tych kątów jest równa 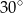 . Wierzchołek kąta
. Wierzchołek kąta 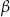 znajduje się w punkcie
znajduje się w punkcie 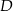 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 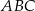 jest równoboczny B)
jest równoboczny B) 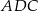 jest prostokątny
jest prostokątny
C) 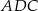 jest równoboczny D)
jest równoboczny D) 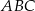 jest prostokątny
jest prostokątny
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 4, wysokość ostrosłupa ma długość 5. Ściana boczna jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 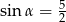 B)
B) 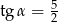 C)
C) 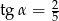 D)
D) 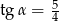
Średnia arytmetyczna ocen Jacka jest równa 3,75, a średnia ocen Karola (liczona z dokładnie tej samej liczby ocen) jest równa 4,25. Średnia ocen obu chłopców jest równa
A) 3,95 B) 4,5 C) 4,0 D) 4,15
Średnia arytmetyczna ocen Zosi jest równa 2,8, a średnia ocen Basi (liczona z dokładnie tej samej liczby ocen) jest równa 4,4. Średnia ocen obu dziewcząt jest równa
A) 3,6 B) 4,0 C) 3,8 D) 4,15
Mniejszą z dwóch liczb spełniających równanie 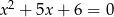 jest
jest
A) -6 B) -3 C) -2 D) -1
Mniejszą z dwóch liczb spełniających równanie 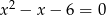 jest
jest
A) -6 B) -3 C) -2 D) -1
Mniejszą z dwóch liczb spełniających równanie 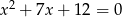 jest
jest
A) -4 B) -3 C) -2 D) -1
Liczba 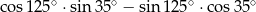 jest równa
jest równa
A) 1 B) 0 C) 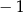 D)
D) 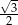
Osią symetrii paraboli będącej wykresem funkcji 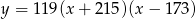 jest prosta o równaniu
jest prosta o równaniu
A) 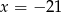 B)
B) 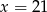 C)
C) 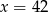 D)
D) 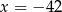
Osią symetrii paraboli będącej wykresem funkcji 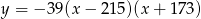 jest prosta o równaniu
jest prosta o równaniu
A) 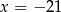 B)
B) 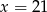 C)
C) 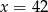 D)
D) 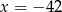
Wartość wyrażenia 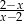 dla
dla 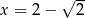 jest równa
jest równa
A) -1 B) 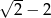 C)
C) 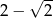 D) 1
D) 1
Wartość wyrażenia 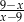 dla
dla 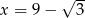 jest równa
jest równa
A) 1 B) 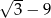 C)
C) 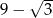 D) -1
D) -1

