Przekrój osiowy stożka jest trójkątem równoramiennym o ramieniu długości 12. Kąt rozwarcia stożka ma miarę 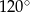 . Objętość stożka wynosi
. Objętość stożka wynosi
A) 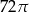 B)
B) 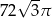 C)
C) 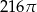 D)
D) 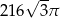
/Szkoła średnia/Zadania testowe
Do wykresu funkcji nie należy punkt 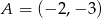 . Funkcja
. Funkcja 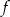 może mieć wzór
może mieć wzór
A) 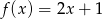 B)
B) 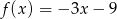 C)
C) 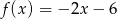 D)
D) 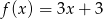
Na podstawie 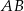 i ramieniu
i ramieniu 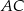 trójkąta równoramiennego
trójkąta równoramiennego 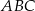 dane są punkty
dane są punkty 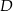 i
i 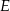 takie, że
takie, że 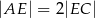 i
i 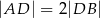 . Punkty
. Punkty 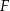 i
i 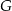 leżą na ramieniu
leżą na ramieniu 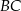 tak, że odcinki
tak, że odcinki 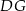 i
i 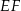 są prostopadłe do prostej
są prostopadłe do prostej 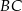 (zobacz rysunek).
(zobacz rysunek).
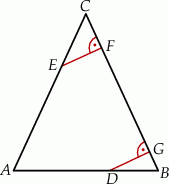
Pole trójkąta 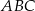 jest równe 18. Zatem suma pól trójkątów
jest równe 18. Zatem suma pól trójkątów 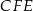 i
i 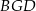 jest równa
jest równa
A) 9 B) 6 C) 3 D) 2
Punkty 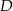 i
i 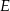 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 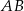 i ramienia
i ramienia 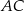 trójkąta równoramiennego
trójkąta równoramiennego 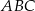 . Punkty
. Punkty 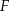 i
i 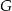 leżą na ramieniu
leżą na ramieniu 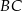 tak, że odcinki
tak, że odcinki 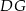 i
i 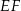 są prostopadłe do prostej
są prostopadłe do prostej 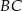 (zobacz rysunek).
(zobacz rysunek).
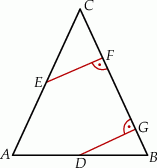
Pole trójkąta 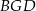 jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta 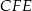 jest równe 4. Zatem pole trójkąta
jest równe 4. Zatem pole trójkąta 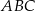 jest równe
jest równe
A) 24 B) 8 C) 12 D) 16
Prosta 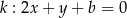 ma dwa punkty wspólne z parabolą
ma dwa punkty wspólne z parabolą 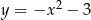 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
A) 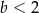 B)
B) 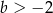 C)
C) 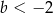 D)
D) 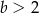
Jeśli 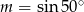 , to
, to
A) 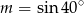 B)
B) 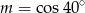 C)
C) 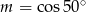 D)
D) 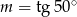
Jeśli 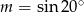 , to
, to
A) 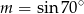 B)
B) 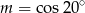 C)
C) 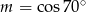 D)
D) 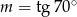
Punkty 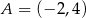 i
i 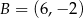 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 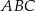 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 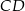 tego trójkąta przecina prostą
tego trójkąta przecina prostą 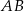 w punkcie
w punkcie
A) 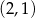 B)
B) 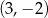 C)
C) 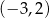 D)
D) 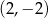
Punkty 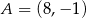 i
i 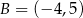 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 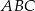 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 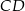 tego trójkąta przecina prostą
tego trójkąta przecina prostą 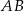 w punkcie
w punkcie
A) 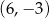 B)
B) 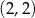 C)
C) 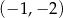 D)
D) 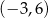
Punkt 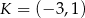 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 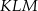 , w którym
, w którym 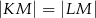 . Odcinek
. Odcinek 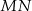 jest wysokością trójkąta i
jest wysokością trójkąta i 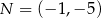 . Zatem
. Zatem
A) 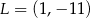 B)
B) 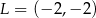 C)
C) 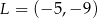 D)
D) 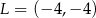
Punkt 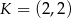 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 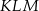 , w którym
, w którym 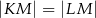 . Odcinek
. Odcinek 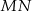 jest wysokością trójkąta i
jest wysokością trójkąta i 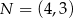 . Zatem
. Zatem
A) 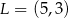 B)
B) 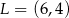 C)
C) 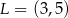 D)
D) 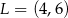
Liczba 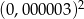 jest równa
jest równa
A) 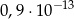 B)
B) 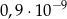 C)
C) 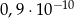 D)
D) 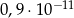
Liczba 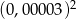 jest równa
jest równa
A) 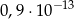 B)
B) 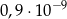 C)
C) 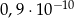 D)
D) 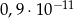
Liczba 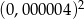 jest równa
jest równa
A) 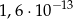 B)
B) 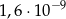 C)
C) 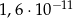 D)
D) 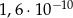
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 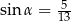 . Bok
. Bok 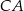 tego trójkąta ma długość:
tego trójkąta ma długość:
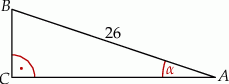
A) 10 B) 24 C) 12 D) 5
Dany jest trójkąt prostokątny o bokach długości 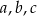 .
.
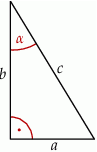
Jeżeli 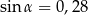 oraz
oraz 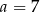 , to
, to
A) 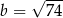 B)
B) 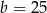 C)
C) 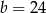 D)
D) 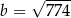
Kąt  w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek
w trójkącie prostokątnym przedstawionym na rysunku spełnia warunek 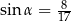 . Bok
. Bok 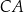 tego trójkąta ma długość:
tego trójkąta ma długość:
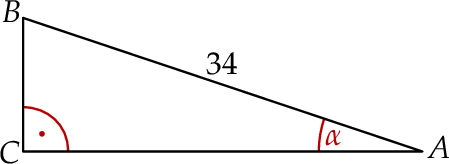
A) 30 B) 8 C) 16 D) 24
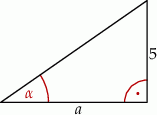
Jeśli 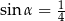 , to długość przyprostokątnej
, to długość przyprostokątnej 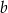 danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
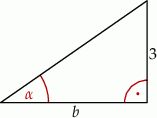
A) 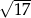 B)
B) 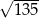 C)
C) 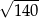 D)
D) 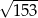
Jeśli 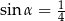 , to długość przyprostokątnej
, to długość przyprostokątnej  danego trójkąta (patrz rysunek) jest równa
danego trójkąta (patrz rysunek) jest równa
A) 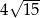 B)
B) 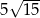 C)
C) 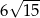 D)
D) 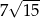
Miara kąta między bokiem 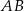 równoległoboku
równoległoboku 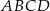 , a przekątną
, a przekątną 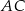 jest równa
jest równa 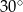 . Długość przekątnej
. Długość przekątnej 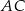 jest równa 5, a długość boku
jest równa 5, a długość boku 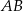 wynosi 4, zatem pole równoległoboku jest równe
wynosi 4, zatem pole równoległoboku jest równe
A) 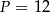 B)
B) 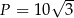 C)
C) 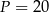 D)
D) 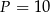
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 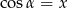 . Wtedy
. Wtedy 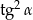 równa się
równa się
A) 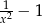 B)
B) 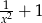 C)
C) 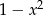 D)
D) 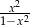
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 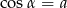 . Wtedy
. Wtedy 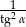 równa się
równa się
A) 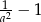 B)
B) 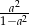 C)
C) 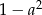 D)
D) 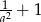
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 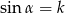 . Wtedy
. Wtedy 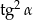 równa się
równa się
A) 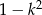 B)
B) 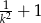 C)
C) 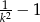 D)
D) 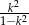
Wyrażenie 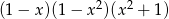 jest równe
jest równe
A) 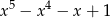 B)
B) 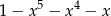 C)
C) 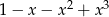 D)
D) 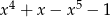
Obwód trójkąta 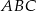 wynosi 28 cm, a jego pole jest równe
wynosi 28 cm, a jego pole jest równe 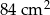 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 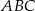 jest równy
jest równy
A) 3 cm B) 6 cm C) 4 cm D) 7 cm
Punkt 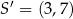 jest obrazem punktu
jest obrazem punktu 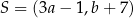 w symetrii osiowej względem osi
w symetrii osiowej względem osi 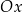 układu współrzędnych, gdy
układu współrzędnych, gdy
A) 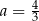 oraz
oraz 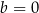 B)
B) 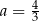 oraz
oraz 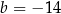
C) 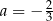 oraz
oraz 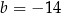 D)
D) 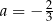 oraz
oraz 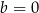
Funkcja kwadratowa 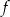 jest określona wzorem
jest określona wzorem 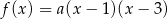 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 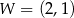 .
.
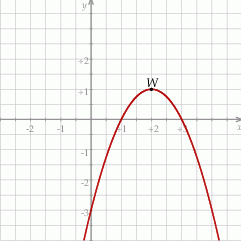
Współczynnik  we wzorze funkcji
we wzorze funkcji 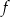 jest równy
jest równy
A) 1 B) 2 C) 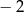 D)
D) 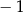
Funkcja kwadratowa 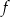 jest określona wzorem
jest określona wzorem 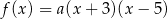 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 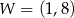 .
.
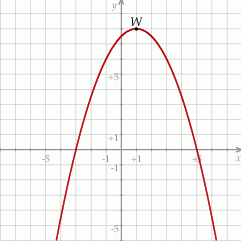
Współczynnik  we wzorze funkcji
we wzorze funkcji 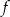 jest równy
jest równy
A) 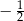 B) 2 C)
B) 2 C) 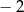 D)
D) 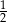
Trójkąt, w którym stosunek długości boków jest równy 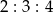 , jest
, jest
A) równoboczny B) prostokątny C) ostrokątny D) rozwartokątny
Trójkąt, w którym stosunek długości boków jest równy 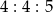 , jest
, jest
A) równoboczny B) prostokątny C) ostrokątny D) rozwartokątny
Do wykresu funkcji 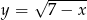 należy punkt
należy punkt 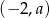 . Wówczas
. Wówczas
A) 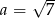 B)
B) 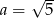 C)
C) 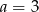 D)
D) 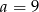
Punkt 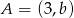 należy do wykresu funkcji
należy do wykresu funkcji 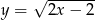 , gdzie
, gdzie 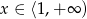 . Wtedy
. Wtedy
A) 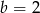 B)
B) 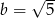 C)
C) 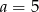 D)
D) 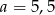
Granica 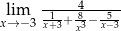
A) jest równa 0 B) jest równa 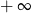 C) jest równa
C) jest równa 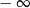 D) nie istnieje
D) nie istnieje
Granica 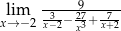
A) jest równa 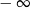 B) jest równa
B) jest równa 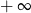 C) nie istnieje D) jest równa 0
C) nie istnieje D) jest równa 0
Liczby rzeczywiste  i
i 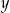 są dodatnie. Wyrażenie
są dodatnie. Wyrażenie 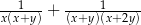 można przekształcić do postaci
można przekształcić do postaci
A) 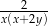 B)
B) 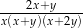 C)
C) 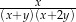 D)
D) 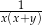
Powierzchnia sześcianu wynosi 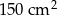 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Powierzchnia sześcianu wynosi 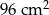 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 4 cm B) 5 cm C) 5,5 cm D) 6 cm
Pole powierzchni całkowitej sześcianu jest równe 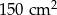 . Długość krawędzi tego sześcianu jest równa
. Długość krawędzi tego sześcianu jest równa
A) 3,5 cm B) 4 cm C) 4,5 cm D) 5 cm
Powierzchnia sześcianu wynosi 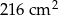 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 3 cm B) 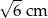 C) 12 cm D) 6 cm
C) 12 cm D) 6 cm
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 6 i niepodzielnych przez 9?
A) 60 B) 120 C) 100 D) 150
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 6 i niepodzielnych przez 4?
A) 150 B) 75 C) 83 D) 68
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 12 i niepodzielnych przez 8?
A) 20 B) 38 C) 75 D) 35

