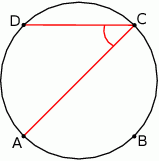
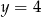Punkty 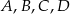 leżą na okręgu o środku
leżą na okręgu o środku 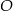 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
A) 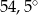 B)
B) 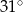 C)
C) 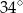 D)
D) 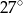
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 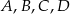 leżą na okręgu o środku
leżą na okręgu o środku 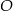 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa

A) 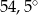 B)
B) 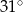 C)
C) 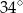 D)
D) 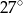
Punkty 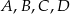 leżą na okręgu o środku
leżą na okręgu o środku 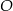 (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
A) 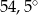 B)
B) 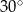 C)
C) 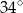 D)
D) 
Liczby całkowite ujemne spełniające nierówność 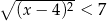 to
to
A) 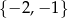 B)
B) 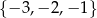
C) 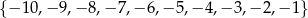 D)
D) 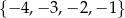
Liczby całkowite ujemne spełniające nierówność 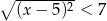 to
to
A) 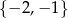 B)
B) 
C) 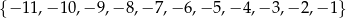 D)
D) 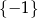
Liczby całkowite ujemne spełniające nierówność 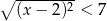 to
to
A) 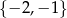 B)
B) 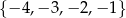
C) 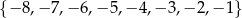 D)
D) 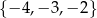
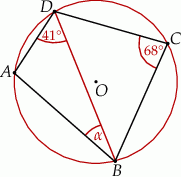
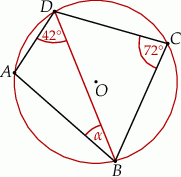
Punkty 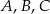 i
i 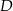 leżą na okręgu o środku
leżą na okręgu o środku 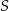 . Miary kątów
. Miary kątów 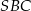 ,
, 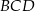 ,
, 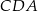 są równe odpowiednio:
są równe odpowiednio: 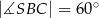 ,
, 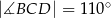 ,
, 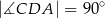 (zobacz rysunek).
(zobacz rysunek).
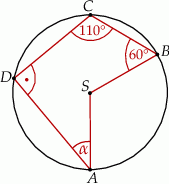
Wynika stąd, że miara  kąta
kąta 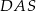 jest równa
jest równa
A) 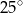 B)
B) 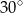 C)
C) 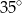 D)
D) 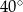
Punkty 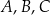 i
i 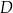 leżą na okręgu o środku
leżą na okręgu o środku 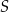 . Miary kątów
. Miary kątów 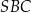 ,
, 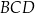 ,
, 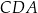 są równe odpowiednio:
są równe odpowiednio: 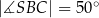 ,
, 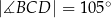 ,
, 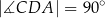 (zobacz rysunek).
(zobacz rysunek).
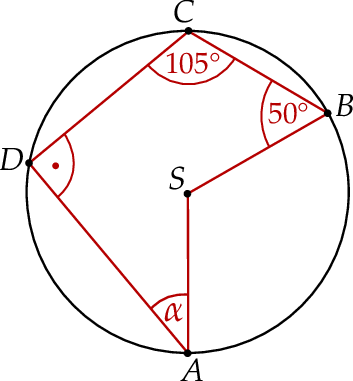
Wynika stąd, że miara  kąta
kąta 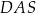 jest równa
jest równa
A) 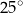 B)
B) 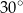 C)
C) 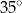 D)
D) 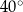
Punkty 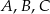 i
i 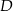 leżą na okręgu o środku
leżą na okręgu o środku 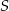 . Miary kątów
. Miary kątów 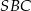 ,
, 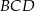 ,
, 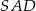 są równe odpowiednio:
są równe odpowiednio: 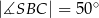 ,
, 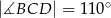 ,
, 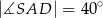 (zobacz rysunek).
(zobacz rysunek).
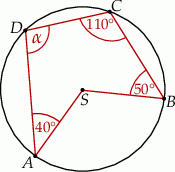
Wynika stąd, że miara  kąta
kąta 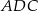 jest równa
jest równa
A) 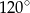 B)
B) 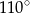 C)
C) 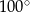 D)
D) 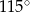
Wskaż równanie okręgu opisanego na trójkącie 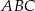 o wierzchołkach
o wierzchołkach 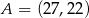 ,
, 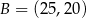 ,
, 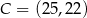
A) 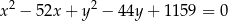 B)
B) 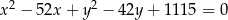
C) 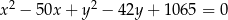 D)
D) 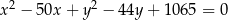
Wielomian 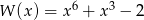 jest równy iloczynowi
jest równy iloczynowi
A) 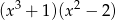 B)
B) 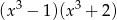 C)
C) 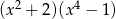 D)
D) 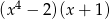
Wielomian 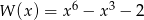 jest równy iloczynowi
jest równy iloczynowi
A) 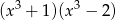 B)
B) 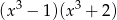 C)
C) 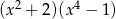 D)
D) 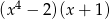
Kostka mydła ma kształt prostopadłościanu. Załóżmy, że po tygodniu używania każdy z wymiarów kostki zmniejszył się o połowę. Pozostała ilość mydła (przy takim samym użytkowaniu) wystarczy na
A) 1 dzień B) 2 dni C) 5 dni D) 7 dni
Przekątna graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 2 razy dłuższa od krawędzi podstawy, jest równa 6. Wynika stąd, że objętość tego graniastosłupa jest równa
A) 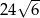 B)
B) 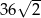 C)
C) 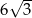 D)
D) 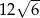
Średnia arytmetyczna liczb: 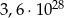 i
i 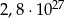 jest równa:
jest równa:
A) 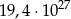 B)
B) 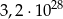 C)
C) 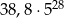 D)
D) 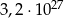
Trójkąt prostokątny ma boki długości 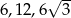 i kąty ostre
i kąty ostre 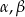 . Kąt
. Kąt 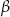 leży naprzeciw boku długości
leży naprzeciw boku długości 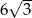 . Zatem
. Zatem
A) 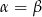 B)
B) 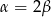 C)
C) 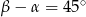 D)
D) 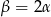
Trójkąt prostokątny ma boki długości 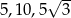 i kąty ostre
i kąty ostre 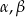 . Kąt
. Kąt 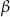 leży naprzeciw boku długości
leży naprzeciw boku długości 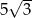 . Zatem
. Zatem
A) 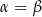 B)
B) 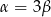 C)
C) 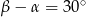 D)
D) 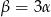
Trójkąt prostokątny ma boki długości 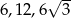 i kąty ostre
i kąty ostre 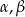 . Kąt
. Kąt 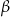 leży naprzeciw boku długości 6. Zatem
leży naprzeciw boku długości 6. Zatem
A) 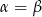 B)
B) 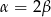 C)
C) 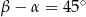 D)
D) 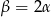
Kąt  jest ostry i
jest ostry i 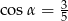 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 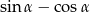 jest równa
jest równa
A) 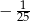 B)
B)  C)
C) 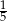 D)
D) 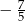
Okrąg o średnicy 6 jest styczny do osi 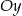 , a oś
, a oś 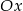 jest jego osią symetrii. Środek tego okręgu ma współrzędne
jest jego osią symetrii. Środek tego okręgu ma współrzędne
A) 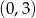 B)
B) 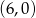 C)
C) 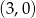 D)
D) 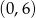
Punkty 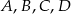 dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego 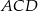 jest równa
jest równa
A) 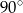 B)
B) 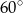 C)
C) 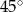 D)
D) 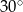
Dana jest funkcja 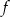 określona wzorem
określona wzorem 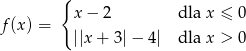
Równanie 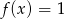 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) cztery rozwiązania. D) pięć rozwiązań.
Dana jest funkcja 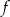 określona wzorem
określona wzorem 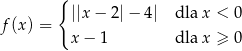
Równanie 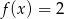 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) cztery rozwiązania. D) pięć rozwiązań.
Dana jest funkcja 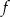 określona wzorem
określona wzorem 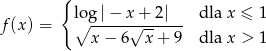
Równanie 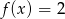 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) trzy rozwiązania. D) cztery rozwiązania.
Dana jest funkcja 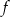 określona wzorem
określona wzorem 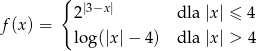
Równanie 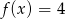 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) trzy rozwiązania. D) cztery rozwiązania.
Liczbą odwrotną do liczby 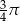 jest liczba:
jest liczba:
A) 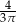 B)
B) 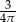 C)
C) 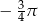 D)
D) 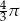
Liczba wszystkich sposobów utworzenia liczb trzycyfrowych o różnych cyfrach ze zbioru 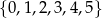 jest równa
jest równa
A) 120 B) 100 C) 60 D) 60
Wszystkich liczb naturalnych trzycyfrowych, w których zapisie dziesiętnym nie występuje cyfra 2, jest
A) 900 B) 729 C) 648 D) 512
Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0, 5, 7, jest
A) 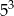 B)
B) 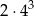 C)
C) 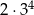 D)
D) 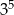
Liczb pięciocyfrowych, które można zapisać tylko za pomocą cyfr 0 i 1, jest
A) 5 B) 10 C) 16 D) 32
Wszystkich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry: 1, 2, 4, 8, 3, jest
A) 200 B) 625 C) 250 D) 500
Wszystkich liczb naturalnych pięciocyfrowych parzystych jest
A) 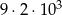 B)
B) 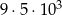 C)
C) 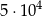 D)
D) 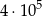
Aby odblokować telefon komórkowy należy użyć czterocyfrowego kodu PIN. Paweł ustalił, że jego kod PIN na parzystych miejscach będzie miał cyfrę nieparzystą, a na nieparzystych miejscach cyfrę parzystą oraz cyfry nie będą się powtarzać. Ile różnych kodów PIN może utworzyć Paweł?
A) 400 B) 300 C) 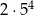 D)
D) 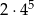
Wszystkich trzycyfrowych liczb naturalnych większych od 300 o wszystkich cyfrach parzystych jest
A) 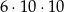 B)
B) 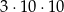 C)
C) 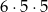 D)
D) 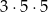
Wszystkich liczb naturalnych trzycyfrowych, w których zapisie dziesiętnym nie występuje cyfra 9, jest
A) 900 B) 648 C) 729 D) 512
Wszystkich różnych liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym wszystkie cyfry są różne, jest
A) 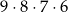 B)
B) 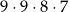 C)
C) 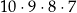 D)
D) 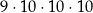
Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0, 3, 5, 7, jest
A) 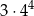 B)
B) 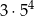 C)
C) 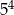 D)
D) 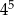
Liczba wszystkich dodatnich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry 0 i 2, jest równa
A) 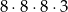 B)
B) 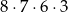 C)
C) 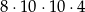 D)
D) 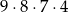
Wszystkich liczb pięciocyfrowych, w których występują wyłącznie cyfry 0, 2, 5, jest
A) 12 B) 36 C) 162 D) 243
Ile jest wszystkich dwucyfrowych liczb naturalnych utworzonych z cyfr: 1, 3, 5, 7, 9, w których cyfry się nie powtarzają?
A) 10 B) 15 C) 20 D) 25
Wszystkich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry: 5, 2, 4, 8, 7, jest
A) 500 B) 625 C) 250 D) 200
Ile jest wszystkich trzycyfrowych liczb naturalnych utworzonych z cyfr: 1, 3, 5, 7, 9, w których cyfry się nie powtarzają?
A) 60 B) 125 C) 120 D) 95
Liczba wszystkich dodatnich liczb czterocyfrowych nieparzystych, w których zapisie nie występują cyfry 1 i 2, jest równa
A) 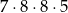 B)
B) 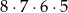 C)
C) 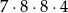 D)
D) 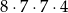
Wszystkich liczb naturalnych sześciocyfrowych nieparzystych jest
A) 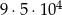 B)
B) 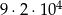 C)
C) 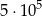 D)
D) 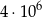
Wszystkich różnych liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym występują cztery różne cyfry parzyste jest
A) 120 B) 96 C) 625 D) 500
Punkt 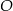 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 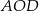 ma miarę
ma miarę
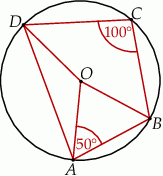
A) 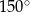 B)
B) 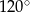 C)
C) 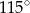 D)
D) 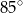
Punkt 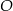 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 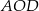 ma miarę
ma miarę
A) 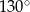 B)
B) 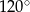 C)
C) 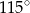 D)
D) 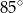
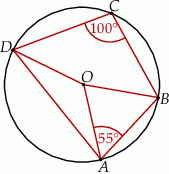
Punkty 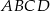 leżą na okręgu o środku
leżą na okręgu o środku 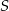 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 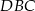 jest równa
jest równa
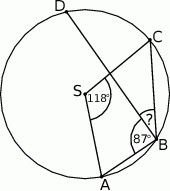
A) 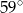 B)
B) 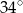 C)
C) 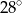 D)
D) 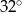
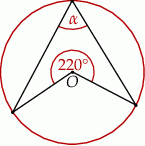
Punkt 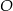 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
A) 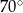 B)
B) 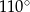 C)
C) 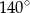 D)
D) 
Punkt 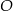 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
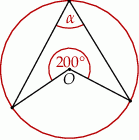
A)  B)
B) 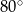 C)
C) 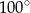 D)
D) 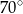
Miara kąta  (patrz rysunek obok) jest równa
(patrz rysunek obok) jest równa
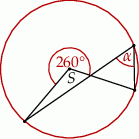
A) 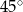 B)
B) 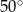 C)
C) 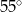 D)
D) 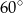
Środek 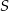 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 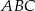 należy do boku
należy do boku 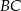 . Suma miar kątów
. Suma miar kątów 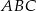 i
i 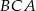 trójkąta
trójkąta 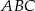 jest równa
jest równa
A) 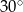 B)
B) 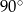 C)
C) 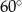 D)
D) 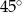
Środek 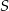 okręgu opisanego na trójkącie
okręgu opisanego na trójkącie 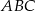 należy do boku
należy do boku 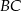 . Miara kąta
. Miara kąta 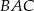 trójkąta
trójkąta 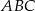 jest równa
jest równa
A) 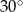 B)
B) 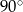 C)
C) 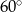 D)
D) 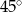
Punkty 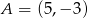 ,
, 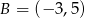 ,
, 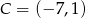 i
i 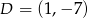 są wierzchołkami prostokąta
są wierzchołkami prostokąta 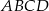 . Pole tego prostokąta jest równe
. Pole tego prostokąta jest równe
A) 16 B) 32 C) 64 D) 96
Jeżeli 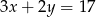 i
i 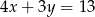 to
to
A) 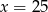 B)
B) 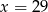 C)
C) 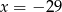 D)
D) 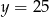
Jeżeli 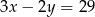 i
i 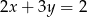 to
to
A) 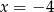 B)
B) 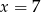 C)
C) 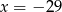 D)
D)