Jacek i Karol rzucają śnieżkami do celu. Jacek trafia do celu średnio trzy razy na dziesięć rzutów, a Karol trafia do celu średnio raz na pięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każdy z chłopców wykona po jednym rzucie jest równe
A) 0,06 B) 0,38 C) 0,56 D) 0,5
/Szkoła średnia/Zadania testowe
Ewa i Kasia rzucają śnieżkami do celu. Ewa trafia do celu średnio raz na pięć rzutów, a Kasia trafia do celu średnio trzy razy na dziesięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każda z dziewcząt wykona po jednym rzucie jest równe
A) 0,5 B) 0,56 C) 0,38 D) 0,06
Liczba 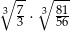 jest równa
jest równa
A) 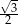 B)
B) 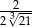 C)
C)  D)
D) 
Liczba 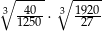 jest równa
jest równa
A) 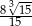 B)
B) 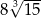 C) 8 D)
C) 8 D) 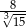
Wartość wyrażenia 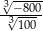 jest równa
jest równa
A) 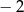 B)
B) 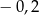 C) 2 D) 0,2
C) 2 D) 0,2
Liczba 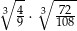 jest równa
jest równa
A)  B)
B) 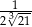 C)
C) 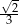 D)
D) 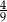
Liczba 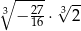 jest równa
jest równa
A) 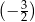 B)
B)  C)
C)  D)
D) 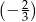
Liczba 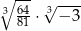 jest równa
jest równa
A) 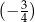 B)
B) 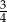 C)
C) 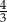 D)
D) 
Para liczb 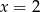 i
i 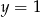 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 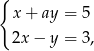 gdy
gdy
A) 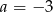 B)
B) 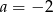 C)
C) 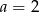 D)
D) 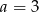
Para liczb 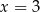 i
i 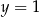 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 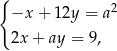 dla
dla
A) 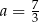 B)
B) 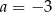 C)
C) 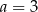 D)
D) 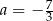
Para liczb 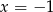 i
i 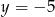 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 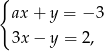 gdy
gdy
A) 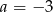 B)
B) 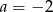 C)
C) 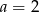 D)
D) 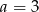
Para liczb 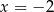 i
i 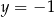 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 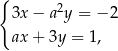 dla
dla
A) 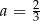 B)
B) 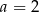 C)
C) 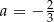 D)
D) 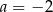
Para liczb 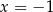 i
i 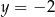 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 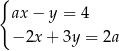 dla
dla
A) 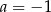 B)
B) 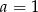 C)
C) 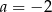 D)
D) 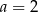
Para liczb 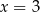 ,
, 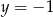 spełnia układ równań
spełnia układ równań
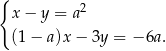
Wtedy  jest równe
jest równe
A) 2 B) 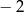 C)
C) 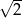 D)
D) 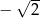
Para liczb 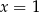 ,
, 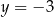 spełnia układ równań
spełnia układ równań
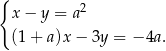
Wtedy  jest równe
jest równe
A) 2 B) 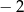 C)
C) 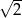 D)
D) 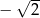
Para liczb 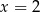 i
i 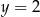 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 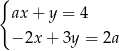 dla
dla
A) 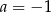 B)
B) 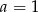 C)
C) 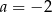 D)
D) 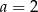
Pochodna funkcji 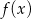 jest równa
jest równa 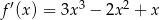 . Funkcja
. Funkcja 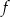 może mieć wzór
może mieć wzór
A) 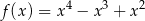 B)
B) 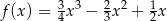
C) 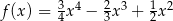 D)
D) 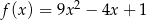
Funkcja 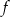 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 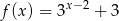 . Prosta
. Prosta 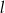 ma równanie
ma równanie 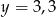 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 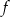 i prosta
i prosta 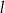 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Funkcja 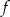 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 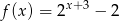 . Prosta
. Prosta 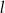 ma równanie
ma równanie 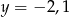 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 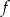 i prosta
i prosta 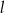 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Prosta 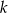 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 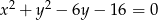 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 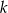 jest równa
jest równa
A) 9 B) 4 C) 25 D) 5
Prosta 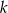 jest styczna do okręgu o równaniu
jest styczna do okręgu o równaniu 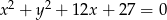 . Odległość środka tego okręgu od prostej
. Odległość środka tego okręgu od prostej 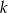 jest równa
jest równa
A) 9 B) 3 C) 25 D) 5
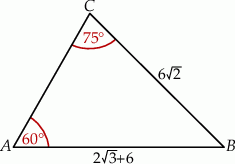
Pole trójkąta 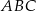 przedstawionego na rysunku jest równe
przedstawionego na rysunku jest równe
A) 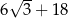 B)
B) 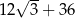 C)
C) 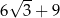 D)
D) 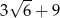
Liczba 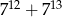 jest podzielna przez
jest podzielna przez
A) 16 B) 6 C) 4 D) 5
Liczba 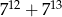 nie jest podzielna przez
nie jest podzielna przez
A) 14 B) 7 C) 8 D) 5
Liczba 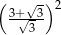 jest równa
jest równa
A) 4 B) 9 C) 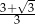 D)
D) 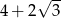
Liczba 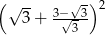 jest równa
jest równa
A) 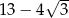 B) 11 C)
B) 11 C) 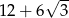 D) 3
D) 3
Liczba 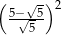 jest równa
jest równa
A) 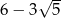 B) 4 C)
B) 4 C) 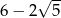 D) 6
D) 6
Liczba 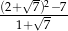 jest równa
jest równa
A) 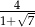 B) 4 C)
B) 4 C) 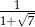 D) 2
D) 2
W układzie współrzędnych dane są punkty 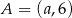 oraz
oraz 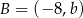 . Punkt
. Punkt 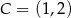 jest takim punktem odcinka
jest takim punktem odcinka  , że
, że 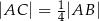 . Wynika stąd, że
. Wynika stąd, że
A) 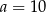 i
i 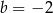 B)
B) 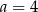 i
i 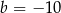 C)
C) 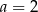 i
i 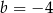 D)
D) 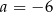 i
i 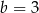
Funkcja 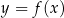 jest określona za pomocą tabeli
jest określona za pomocą tabeli
 | 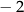 | 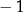 | 0 | 1 | 2 |
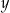 | 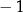 | 0 | 1 | 0 | 3 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 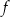 ma dokładnie jedno miejsce zerowe. ma dokładnie jedno miejsce zerowe. | P | F |
Wykres funkcji 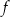 jest symetryczny względem osi jest symetryczny względem osi 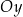 . . | P | F |
Funkcja 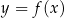 jest określona za pomocą tabeli
jest określona za pomocą tabeli
 | 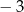 | 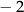 | 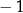 | 0 | 1 | 2 | 3 |
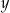 | 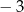 | 2 | 0 | 1 | 0 | 2 | 1 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 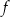 ma dokładnie jedno miejsce zerowe. ma dokładnie jedno miejsce zerowe. | P | F |
W kartezjańskim układzie współrzędnych 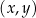 wykres funkcji wykres funkcji 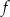 jest symetryczny względem osi jest symetryczny względem osi 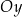 . . | P | F |
Największa wartość funkcji 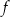 jest równa 3. jest równa 3. | P | F |
Dany jest kwadrat o przekątnej 6. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 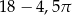 B)
B) 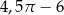 C)
C) 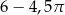 D)
D) 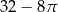
Dany jest kwadrat o przekątnej 2. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 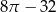 B)
B) 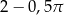 C)
C) 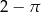 D)
D) 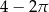
Dany jest kwadrat o przekątnej 4. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 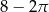 B)
B) 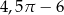 C)
C) 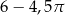 D)
D) 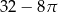
Pole trójkąta 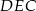 wynosi
wynosi 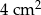 . Wiadomo, że
. Wiadomo, że 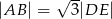 oraz
oraz 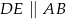 . Zatem pole trójkąta
. Zatem pole trójkąta 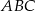 jest równe
jest równe
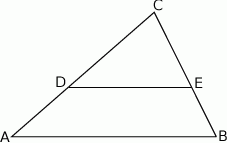
A) 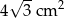 B)
B) 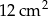 C)
C) 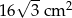 D)
D) 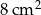
Prosta 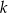 przecina oś
przecina oś 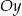 układu współrzędnych w punkcie
układu współrzędnych w punkcie 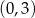 i jest prostopadła do prostej o równaniu
i jest prostopadła do prostej o równaniu 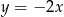 . Wówczas prosta
. Wówczas prosta 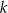 przecina oś
przecina oś 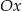 układu współrzędnych w punkcie
układu współrzędnych w punkcie
A) 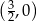 B)
B) 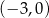 C)
C) 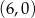 D)
D) 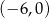
Przekątna przekroju osiowego walca jest o 13 dłuższa od promienia podstawy tego walca, oraz o 2 dłuższa od jego wysokości. Pole podstawy tego walca jest równe
A) 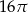 B)
B) 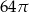 C)
C) 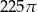 D)
D) 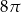
Promień 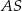 podstawy walca jest równy wysokości
podstawy walca jest równy wysokości 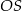 tego walca. Sinus kąta
tego walca. Sinus kąta 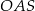 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
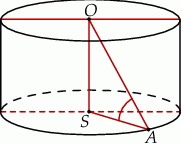
A) 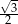 B)
B) 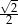 C)
C) 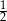 D) 1
D) 1
Promień 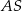 podstawy walca jest równy wysokości
podstawy walca jest równy wysokości 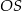 tego walca. Tangens kąta
tego walca. Tangens kąta 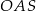 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
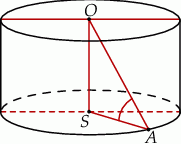
A) 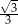 B)
B) 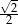 C)
C) 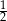 D) 1
D) 1
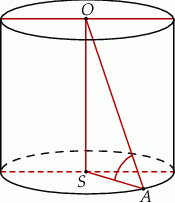
Promień 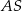 podstawy walca jest równy połowie wysokości
podstawy walca jest równy połowie wysokości 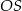 tego walca. Sinus kąta
tego walca. Sinus kąta 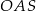 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 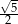 B)
B) 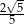 C)
C) 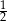 D) 1
D) 1
Granica jednostronna 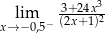 jest równa
jest równa
A) 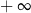 B) 9 C) 0 D)
B) 9 C) 0 D) 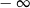
Funkcja 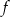 określona jest wzorem
określona jest wzorem 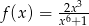 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 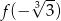 jest równa
jest równa
A) 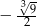 B)
B) 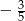 C)
C)  D)
D) 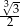
Funkcja 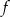 określona jest wzorem
określona jest wzorem 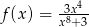 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 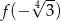 jest równa
jest równa
A) 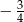 B)
B) 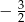 C)
C) 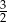 D)
D) 
Funkcja 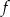 określona jest wzorem
określona jest wzorem 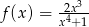 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 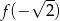 jest równa
jest równa
A) 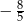 B)
B) 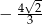 C)
C) 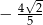 D)
D) 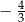
Interpretacją geometryczną układu równań 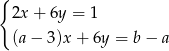 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 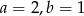 B)
B) 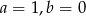 C)
C) 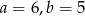 D)
D) 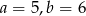
Interpretacją geometryczną układu równań 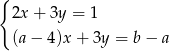 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 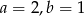 B)
B) 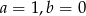 C)
C) 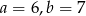 D)
D) 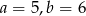
Interpretacją geometryczną układu równań 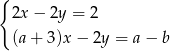 są dwie proste pokrywające się. Zatem
są dwie proste pokrywające się. Zatem
A) 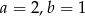 B)
B) 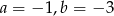 C)
C) 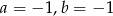 D)
D) 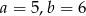
Stosunek boków prostokąta jest równy 1:2. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 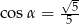 B)
B) 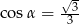 C)
C) 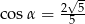 D)
D) 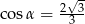
Stosunek boków prostokąta jest równy 2:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 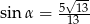 B)
B) 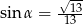 C)
C) 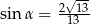 D)
D) 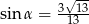
Stosunek boków prostokąta jest równy 1:2. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 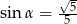 B)
B) 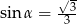 C)
C) 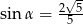 D)
D) 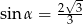
Stosunek boków prostokąta jest równy 1:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 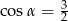 B)
B) 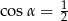 C)
C) 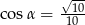 D)
D) 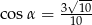
Stosunek boków prostokąta jest równy 2:3. Przekątna prostokąta tworzy z dłuższym bokiem prostokąta kąt  , taki, że
, taki, że
A) 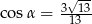 B)
B) 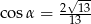 C)
C) 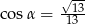 D)
D)