Punkt 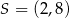 jest środkiem odcinka
jest środkiem odcinka 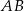 , gdzie
, gdzie 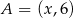 i
i 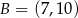 dla
dla  równego
równego
A) 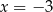 B)
B) 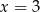 C)
C) 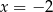 D)
D) 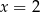
/Szkoła średnia/Zadania testowe
Właściciel sklepu z zabawkami przeprowadził lokalne badanie rynkowe dotyczące wpływu zmiany ceny zestawu klocków na liczbę kupujących ten produkt. Z badania wynika, że dzienny przychód 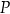 ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o
ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o  zł, wyraża się wzorem
zł, wyraża się wzorem
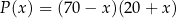
gdzie  jest liczbą całkowitą spełniającą warunki
jest liczbą całkowitą spełniającą warunki 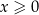 i
i 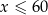 . Dzienny przychód ze sprzedaży zestawów klocków będzie równy 800 zł, gdy liczba
. Dzienny przychód ze sprzedaży zestawów klocków będzie równy 800 zł, gdy liczba  jest równa
jest równa
A) 25 B) 30 C) 45 D) 50 E) 60
Wyrażenie 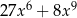 można zapisać w postaci
można zapisać w postaci
A) 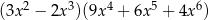 B)
B) 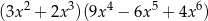
C) 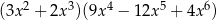 D)
D) 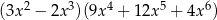
Zbiorem rozwiązań nierówności 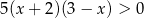 jest zbiór zaznaczony na osi liczbowej:
jest zbiór zaznaczony na osi liczbowej:

Zbiorem rozwiązań nierówności 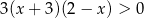 jest zbiór zaznaczony na osi liczbowej:
jest zbiór zaznaczony na osi liczbowej:

Zbiorem rozwiązań nierówności 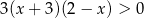 jest zbiór zaznaczony na osi liczbowej:
jest zbiór zaznaczony na osi liczbowej:

Wiadomo, że 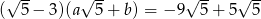 oraz
oraz  i
i 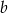 są liczbami wymiernymi. Zatem
są liczbami wymiernymi. Zatem
A) 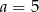 i
i 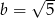 B)
B) 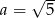 i
i 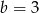 C)
C) 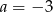 i
i 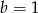 D)
D) 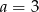 i
i 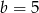
Wiadomo, że 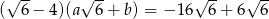 oraz
oraz  i
i 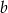 są liczbami wymiernymi. Zatem
są liczbami wymiernymi. Zatem
A) 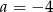 i
i 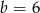 B)
B) 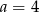 i
i 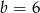 C)
C) 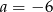 i
i 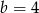 D)
D) 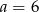 i
i 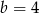
Wiadomo, że 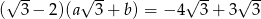 oraz
oraz  i
i 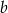 są liczbami wymiernymi. Zatem
są liczbami wymiernymi. Zatem
A) 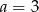 i
i 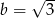 B)
B) 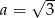 i
i 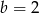 C)
C) 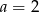 i
i 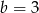 D)
D) 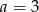 i
i 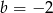
Wykresem funkcji kwadratowej 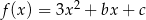 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 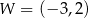 . Wzór tej funkcji w postaci kanonicznej to
. Wzór tej funkcji w postaci kanonicznej to
A) 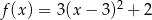 B)
B) 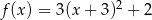
C) 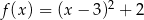 D)
D) 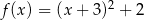
Dane są punkty 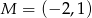 i
i 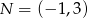 . Punkt
. Punkt 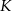 jest środkiem odcinka
jest środkiem odcinka 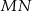 . Obrazem punktu
. Obrazem punktu 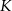 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 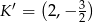 B)
B) 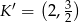 C)
C) 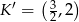 D)
D) 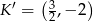
Dane są punkty 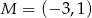 i
i 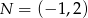 . Punkt
. Punkt 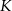 jest środkiem odcinka
jest środkiem odcinka 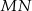 . Obrazem punktu
. Obrazem punktu 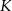 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 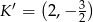 B)
B) 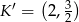 C)
C) 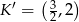 D)
D) 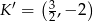
Funkcja 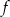 jest określona wzorem
jest określona wzorem 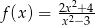 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 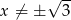 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 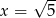 jest równa
jest równa
A) 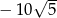 B)
B) 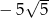 C)
C) 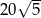 D)
D) 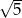
Funkcja 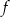 jest określona wzorem
jest określona wzorem 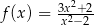 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 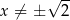 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 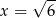 jest równa
jest równa
A) 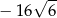 B)
B) 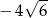 C)
C) 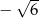 D)
D) 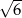
Wykresem funkcji kwadratowej 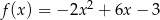 jest parabola, której wierzchołkiem jest punkt o współrzędnych
jest parabola, której wierzchołkiem jest punkt o współrzędnych
A) 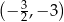 B)
B) 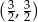 C)
C) 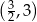 D)
D) 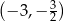
Wyrażenie 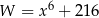 jest równe
jest równe
A) 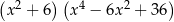 B)
B) 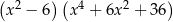
C) 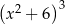 D)
D) 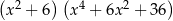
Wyrażenie 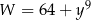 jest równe
jest równe
A) 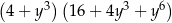 B)
B) 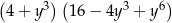
C) 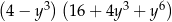 D)
D) 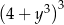
Wyrażenie 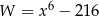 jest równe
jest równe
A) 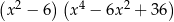 B)
B) 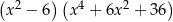
C) 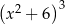 D)
D) 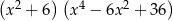
Wyrażenie 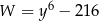 jest równe
jest równe
A) 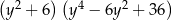 B)
B) 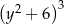
C) 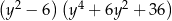 D)
D) 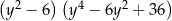
Wyrażenie 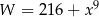 jest równe
jest równe
A) 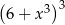 B)
B) 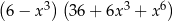
C) 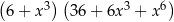 D)
D) 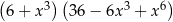
Wyrażenie 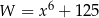 jest równe
jest równe
A) 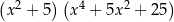 B)
B) 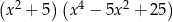
C) 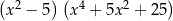 D)
D) 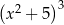
Wyrażenie 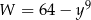 jest równe
jest równe
A) 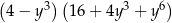 B)
B) 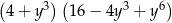
C) 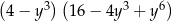 D)
D) 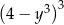
Wyrażenie  jest równe
jest równe
A) 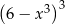 B)
B) 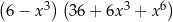
C) 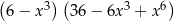 D)
D) 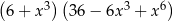
Wyrażenie 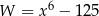 jest równe
jest równe
A) 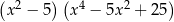 B)
B) 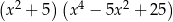
C) 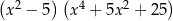 D)
D) 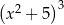
Wyrażenie 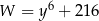 jest równe
jest równe
A) 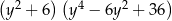 B)
B) 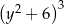
C) 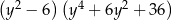 D)
D) 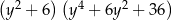
Rozwiązaniem układu równań 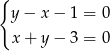 jest para
jest para
A) 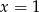 i
i 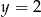 B)
B) 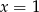 i
i 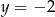 C)
C) 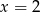 i
i 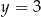 D)
D) 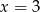 i
i 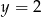
Układ równań 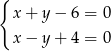 opisuje w układzie współrzędnych na płaszczyźnie punkt
opisuje w układzie współrzędnych na płaszczyźnie punkt
A) 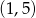 B)
B) 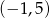 C)
C) 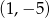 D)
D) 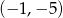
Rozwiązaniem układu równań 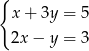 jest
jest
A) 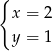 B)
B) 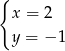 C)
C) 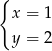 D)
D) 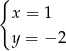
Rozwiązaniem układu równań 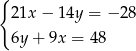 jest para liczb
jest para liczb
A) 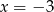 i
i 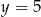 B)
B) 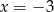 i
i 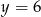 C)
C) 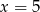 i
i 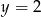 D)
D) 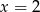 i
i 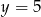
Dany jest układ równań
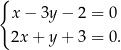
Rozwiązaniem tego układu równań jest para liczb
A) 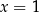 i
i 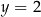 B)
B) 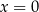 i
i 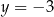 C)
C) 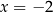 i
i 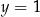 D)
D) 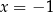 i
i 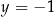
Dany jest układ równań
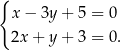
Rozwiązaniem tego układu równań jest para liczb
A) 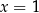 i
i 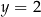 B)
B) 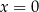 i
i 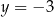 C)
C) 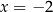 i
i 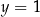 D)
D) 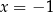 i
i 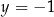
Rozwiązaniem układu równań 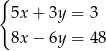 jest para liczb
jest para liczb
A) 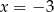 i
i 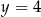 B)
B) 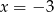 i
i 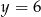 C)
C) 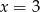 i
i 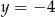 D)
D) 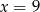 i
i 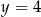
Rozwiązaniem układu równań 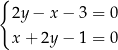 jest para
jest para
A) 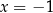 i
i 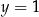 B)
B) 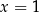 i
i 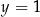 C)
C) 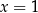 i
i 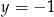 D)
D) 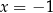 i
i 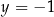
Rozwiązaniem układu równań 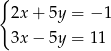 jest
jest
A) 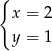 B)
B) 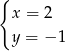 C)
C) 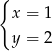 D)
D) 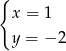
Wierzchołek paraboli ma współrzędne 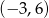 . Punkt
. Punkt 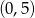 należy do paraboli. Zbiorem wartości funkcji jest
należy do paraboli. Zbiorem wartości funkcji jest
A) 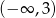 B)
B) 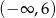 C)
C) 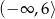 D)
D) 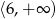
Granica 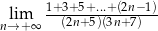 jest równa
jest równa
A) 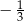 B)
B) 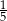 C)
C) 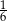 D) 0
D) 0
Wartość liczbowa wyrażenia 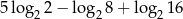 jest równa
jest równa
A) 1 B) 2 C) 6 D) 8
Wartość liczbowa wyrażenia 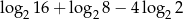 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Dany jest ciąg 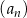 określony wzorem
określony wzorem 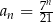 dla każdej liczby naturalnej
dla każdej liczby naturalnej 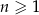 . Pięćdziesiątym wyrazem ciągu
. Pięćdziesiątym wyrazem ciągu 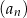 jest
jest
A) 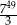 B)
B) 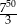 C)
C) 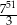 D)
D) 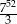
Ciąg 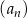 jest określony wzorem
jest określony wzorem 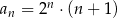 dla każdej liczby naturalnej
dla każdej liczby naturalnej 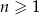 . Wyraz
. Wyraz 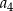 jest równy
jest równy
A) 64 B) 40 C) 48 D) 80
Ciąg 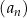 jest określony wzorem
jest określony wzorem 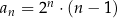 dla każdej liczby naturalnej
dla każdej liczby naturalnej 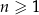 . Wyraz
. Wyraz 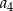 jest równy
jest równy
A) 64 B) 40 C) 48 D) 80
Pan Jakub ma 4 marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 21 C) 28 D) 70
Pan Tomasz ma 5 marynarek, 9 par różnych spodni i 6 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 20 B) 45 C) 280 D) 270
Pan Jakub ma 8 marynarek, 5 par różnych spodni i 9 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 240 B) 22 C) 360 D) 90
Andrzej ma w szafie 4 koszule: czerwoną, żółtą, zieloną i niebieską; 3 pary spodni: niebieskie, czarne i szare; oraz 5 par butów: czarne, szare, zielone, czerwone i niebieskie. Andrzej wybiera z szafy zestaw ubrania: jedną koszulę, jedną parę spodni i jedną parę butów. Zestawy ubrania wybierane przez Andrzeja określimy jako różne, gdy będą różniły się kolorem chociaż jednego rodzaju elementu ubioru w zestawie. Liczba wszystkich możliwych, różnych zestawów ubrania, jakie może wybrać Andrzej, jest równa
A) 12 B) 72 C) 60 D) 720
Pan Łukasz ma 3 marynarki, 8 par różnych spodni i 11 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 280 B) 22 C) 132 D) 264
Jeśli 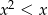 , to
, to
A) 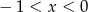 B)
B) 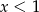 C)
C) 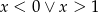 D)
D) 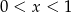
Jeśli 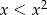 , to
, to
A) 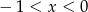 B)
B) 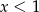 C)
C) 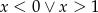 D)
D) 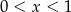
Jeśli 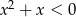 , to
, to
A) 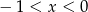 B)
B) 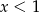 C)
C) 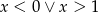 D)
D) 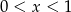
Jeśli 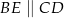 oraz
oraz 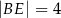 ,
, 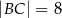 i
i 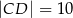 (patrz rysunek),
(patrz rysunek),
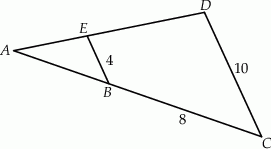
to długość odcinka 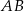 jest równa
jest równa
A) 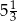 B)
B) 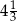 C)
C) 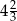 D)
D) 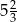
Suma 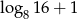 jest równa
jest równa
A) 3 B)  C)
C) 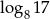 D)
D) 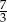
Suma 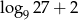 jest równa
jest równa
A) 5 B)  C)
C) 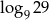 D)
D) 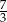
Liczba 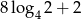 jest równa
jest równa
A) 8 B) 6 C) 4 D) 3,5
Suma 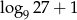 jest równa
jest równa
A) 3 B)  C)
C) 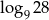 D)
D) 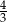
Jednym z pierwiastków równania 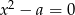 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 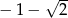 . Zatem liczba
. Zatem liczba  jest równa:
jest równa:
A) 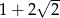 B)
B) 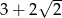 C)
C) 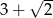 D) 0
D) 0

